- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Integration by Parts Homework: Get Help Now
- Thread starter uzman1243
- Start date
In summary, the conversation is about using integration by parts for a given sum involving a function I(n). The suggestion is to try to determine the function for discrete values of n and use the substitution u = sin(n-1)(x) and dv = sin(x) dx. The conversation also includes a hint for solving the problem and a question about the choice of u.
Physics news on Phys.org
- #2
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,811
- 1,671
First of all, I(n) is not a sum. I is a function which depends on the exponent of the sine function in the integrand.
You might try to determine what I(n) is for some discrete values of n, like n = 2, 3, 4, etc. and see if a pattern emerges.
You might try to determine what I(n) is for some discrete values of n, like n = 2, 3, 4, etc. and see if a pattern emerges.
- #3
SammyS
Staff Emeritus
Science Advisor
Homework Helper
Gold Member
- 11,886
- 1,477
What sum ?uzman1243 said:Homework Statement
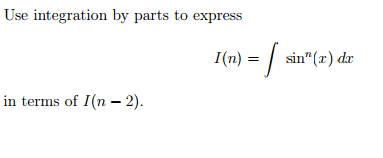
Homework Equations
N/A
The Attempt at a Solution
I can't even begin the attempt because I don't know how you could use intergration by parts for this sum in the first place.
Can you help me out?
Let u = sin(n-1)(x), and dv = sin(x) dx
(The King beat me by fractions of a minute!)
- #4
lurflurf
Homework Helper
- 2,461
- 158
hint
$$\int\! \sin^n(x) \, \mathrm{d}x=\int\! \sin^{n-2}(x)\sin^{2}(x) \, \mathrm{d}x=\int\! \sin^{n-2}(x)\big(1-\cos^{2}(x)\big) \, \mathrm{d}x$$
$$\int\! \sin^n(x) \, \mathrm{d}x=\int\! \sin^{n-2}(x)\sin^{2}(x) \, \mathrm{d}x=\int\! \sin^{n-2}(x)\big(1-\cos^{2}(x)\big) \, \mathrm{d}x$$
- #5
mafagafo
- 188
- 12
This does not look like precalculus.
- #6
uzman1243
- 80
- 1
SammyS said:What sum ?
Let u = sin(n-1)(x), and dv = sin(x) dx
(The King beat me by fractions of a minute!)
Lol. He did.
Anyways, can you tell me why sin(n-1)(x)?
- #7
SammyS
Staff Emeritus
Science Advisor
Homework Helper
Gold Member
- 11,886
- 1,477
(n-1) is half way from n to (n-2) .uzman1243 said:Lol. He did.
Anyways, can you tell me why sin(n-1)(x)?
Try it and see what happens !
1. What is the purpose of Integration by Parts?
Integration by Parts is a technique used in calculus to solve integrals that cannot be solved by basic integration rules. It allows us to break down a complex integral into simpler parts to make it easier to solve.
2. How do I know when to use Integration by Parts?
You should use Integration by Parts when you have an integral that involves a product of two functions, and the integral cannot be solved by any other method. This usually occurs when one function is becoming simpler while the other is becoming more complex.
3. What are the steps for using Integration by Parts?
The steps for Integration by Parts are as follows: (1) Identify the two functions in the integral, (2) choose "u" and "dv" such that the integral of "dv" can be easily solved, (3) use the formula "∫u dv = uv - ∫v du" to solve the integral, (4) repeat the process until the integral is fully solved.
4. Can Integration by Parts be used for definite integrals?
Yes, Integration by Parts can be used for definite integrals. In this case, the formula becomes "∫a to b u dv = [uv]a to b - ∫a to b v du".
5. Are there any common mistakes to avoid when using Integration by Parts?
One common mistake to avoid is choosing "u" and "dv" incorrectly. "u" should be chosen as the function that becomes simpler after each integration, and "dv" should be the function that becomes more complex. Another mistake is forgetting to include the "±C" when integrating "v du" in the formula.
Similar threads
-
Calculus and Beyond Homework Help
- Replies
- 4
- Views
- 615
-
Calculus and Beyond Homework Help
- Replies
- 13
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 1
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 18
- Views
- 2K
-
Calculus and Beyond Homework Help
- Replies
- 5
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 9
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 24
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 13
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 1
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 5
- Views
- 1K
Share: