Is the Changing Clock Rate in Relativity Directionally Dependent?

[pervect]

Here's an example of the sorts of problems that arise with accelerated observers.

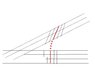
Attached is a crude drawing of a space-time diagram. The thick red line represents an observer who accelerates briefly (time runs up the page), then stops accelerating. ([clarify] - He maintains his velocity that he picked up while he was acclerating). The section where he accelerates is dotted.

The black lines represent the initial coordinate system of the oberver. Horizontal lines represent his notion of "simultaneous events".

The blue lines represent the new coordianate system of the observer after he accelerates, then stops. Note that his defintion of simultaneous events changes after he accelerates (the blue lines representing simultaneous events, are no longer horizontal, but tilted).

We assume that the observer wants to use coordinates that are compatible with both his initial coordiante system (before he accelerates), and his new coordinate system (after he accelerates) to define his coordiante system.

In a well behaved coordiante system, an event is defined by a pair of coordinates which are unique. Thus lines of simultaneity can never cross, i.e. events where t=0 are always different from events where t=1, and the lines in the space-time diagram defined by "t=0" and by "t=1' never cross.

You can see, however, that the black lines do cross the blue lines!

There is no problem in the neighborhood of the observer, but it is not possible to define a well-behaved global coordinate system for our "briefly accelerated observer" when the region coverd becomes large enough.

 

[yogi]

I would concur that the frame attached to the clock in orbit must be local - at least from the standpoint of academic purity. I would also say that the analogy to the round trip twin is appropriate - in fact Einstein in his description in Part 4 referred both to a time discrepency for a round trip version and a one way vesion. So even if the free float frame has its limitations as an inertial frame - it is of no significance - there is little or no difference between doing the experiment using a circular orbit or replacing the Earth with a zero mass anchor point and tethering a rocket ship which travels the same path w/o gravity - i.e, the Eucledean space version previously raised as a question answered by pervect. What is at issue is why identical clocks record different times - we do not have to bring them together to examine them (although that is one way) but we can continually interrogate the moving clock wrt to the ground clock - and we will find that the clock put in motion falls behind - it is not an answer to say - the path length through space-time is different - we already know that - but how does the clock know its been put in motion after it has been synchronized. The fact that each clock runs at its proper rate in its own rest frame also tells nothing - there is an intrinsic difference between the rate of the Earth clock and the moving clock - whether it be in orbit or traveling the same path in Eucledean flat space - the error is small - The difference between the two clocks is given by the SR relationships between moving frames. SR is quite adequate to the job of predicting the time loss. So, while I proposed an orbit to dispell the argument that GR is a factor - there will always be those that claim otherwise, but it does not answer the question.

 

[Hurkyl]

If I have two pieces of string that begin and end at the same point, and I measure their lengths, should I be surprised if I find the strings have different lengths? And does this require an explanation of why the strings have different lengths?

I would answer no, and no.


Conversely, if I have two observers who start and end at the same point in space-time, and I measure the duration of their paths, should I be surprised to find they have different duration? And does this require an explanation of why the paths have different durations?

I would answer no, and no.


You disagree at least with the last question of this group. So let me ask you this: why do you think an explanation is warranted?

Different paths have different duration -- this should not be surprising. The only reason I could imagine that one would think that an explanation would be required is if you had some reason to think they ought to have the same duration.

E.G. if you adhered to some notion of universal tile. (As you tend to do -- you habitually ignore qualifying anything relative, and you often devise experiments so that all observers are making their measurements according to the same coordinate system... such as when you suggested that the oribiting clock should be reading the times on the network of tower clocks)

What is at issue is why identical clocks record different times - we do not have to bring them together to examine them (although that is one way)

How do you plan to go about examining them?

But that's just a tangential issue: what matters (to me) is how you plan on comparing them.

 

[RandallB]

What?

In a well behaved coordiante system, an event is defined by a pair of coordinates which are unique. Thus lines of simultaneity can never cross, i.e. events where t=0 are always different from events where t=1, and the lines in the space-time diagram defined by "t=0" and by "t=1' never cross.

To be a little clearer; I think you mean to ID the original ref frame as drawn in black with time lines t=0 & t=1. And a second ref frame ID as “primed” and blue with time lines t’=0 & t’=1.

Then you say:

You can see, however, that the black lines do cross the blue lines!

. . . it is not possible to define a well-behaved global coordinate system . . . when the region coverd becomes large enough.

What do you expect, of course a “well-behaved global coordinate system” will cross!
They are straight lines and don’t overlap; therefore they have to meet once!
The important point is THEY ONLY CROSS ONCE!
You only have a problem if you get these straight lines of SR relationships to cross TWICE!
That’s all yogi is doing – somewhere he has an error in his math or calculations that is giving him a point where these straight lines cross twice that’s all.
Till he can find where and how he is doing that, he won’t make any progress in moving from SR onto GR.
Confusing these simple SR issues by fussing over “brief accelerations” just distracts form the SR problem he is been having for so long.
GR issues are easily removed for SR problems by just using “Light Speed” (instant) transfers from one ref frame to the other (That means ZERO time change during a transfer that takes zero time in both frames).

Staying with the linear relationships (as shown by the straight lines in your graph) and CORRECTLY detailing all the times and locations as seen from all locations in BOTH reference frames is all that’s needed to get clear on SR “simultaneity”.
In yogi’s case, as I recommended earlier, one weekend on his own, NO beers! (Maybe one Barleywine) and he can “get it” right quick.
Till he can get that part understood; GR, Accelerations, local vs. non-local, and Rotations are just going to confuse the issue for him. Plus I don’t see how anyone can help him till he does this part of the work correctly in his own opinion, by crosschecking his own work. He certainly isn’t going to change the minds of the many here that have done the work and do “get it”.

My best advice for yogi – stay focused on SR alone till you either “get it”.
OR; On the chance that you really do know better, before you will having any credibility in discussing GR etc., you need to detail what you “know better” about SR, in a Logical and Complete explanation convincing enough to change the mind of at least one mentor. Till then don’t waste your time on GR, you will only get frustrated in long threads like this one.

 

[Hurkyl]

To be a little clearer; I think you mean to ID the original ref frame as drawn in black with time lines t=0 & t=1. And a second ref frame ID as “primed” and blue with time lines t’=0 & t’=1.

No, he meant to say they are the same frame. He's talking about a (hypothetical) globally defined non-inertial coordinate system... specifically, one that starts and ends looking like an inertial coordinate system.

So what you see in the picture is the black lines for t=0,1,2,3, and the blue lines for t=8,9,10

They are straight lines and don’t overlap; therefore they have to meet once!
The important point is THEY ONLY CROSS ONCE!

They can, in fact, meet zero times, and the fact they do meet once is a big deal! Because, in the diagram, the same event in space-time can be listed at two different coordinate times!


Incidentally, when I talk about time running backwards at distant places in what I call accelerated reference frames, I'm talking about the phenomena prevect is describing here.

 

[pervect]

What? To be a little clearer; I think you mean to ID the original ref frame as drawn in black with time lines t=0 & t=1. And a second ref frame ID as “primed” and blue with time lines t’=0 & t’=1.

No, I meant what I said. Check out for instance MTW's "Gravitation", pg 168, section $6.3 entitled "Constraints on the size of an accelerated frame".

This is essentially a redrawing of their figure 6.2.

The intent is to explore to what extent it is possible to construct a "natural" coordinate system for a briefly accelerated observer, as a specific example which illustrates some unexpected problems in generalizing the notion of a natural coordinate system. We know that when an observer is not accelerated he has a natural coordinate system given by his inertial frame, so we ask if this idea can be extended to arbitrary observers.

If the briefly accelerated observer has a natural coordinate system, we can quite naturally require that it should be the same as the natural inertial coordinate system he has during the interval before he accelerated, and it should again be the same as his new inertial coordinate system he has after he stops accelerating.

At this point we haven't attempted to address the issue of what coordinates to use while he is accelerating, because the two requirements above already overconstrain the problem.

As the diagram illustrates,we cannot define a consistent uni-valued coordinate system that covers all of space-time and is consistent with both of the inertial coordinate systems that we have demanded it be consistent with. The best we can do is to define such a coordinate system that covers a limited, local region of space-time.

 

[RandallB]

No, I meant what I said. Check out for instance MTW's "Gravitation", pg 168, section $6.3 entitled "Constraints on the size of an accelerated frame".

Who is MTW ?
This looks to me like miss applying GR to an SR graph. But if I can find it I’ll take a look.

 

[Garth]

Who is MTW ?

Misner, Thorne & Wheeler, their textbook, https://www.amazon.com/gp/product/0716703440/?tag=pfamazon01-20, is a standard text of post-graduate gravitation and GR studies.

Garth

 

[RandallB]

Misner, Thorne & Wheeler, gravitation and GR studies.

Thanks –Wow, Expensive for a book from 1973,
found where I can borrow one tonight.

 

[JesseM]

I would concur that the frame attached to the clock in orbit must be local - at least from the standpoint of academic purity.

If you agree it's local, then do you understand this means you can't ask how fast the tower clock is ticking "in the orbiting clock's frame" once they are no longer at the same position?

there is little or no difference between doing the experiment using a circular orbit or replacing the Earth with a zero mass anchor point and tethering a rocket ship which travels the same path w/o gravity - i.e, the Eucledean space version previously raised as a question answered by pervect.

In this case, one clock is moving inertially and the other is not, so you can't ask how fast the tower clock is ticking in the orbiting clock's frame, because the orbiting clock doesn't have a single rest frame.

What is at issue is why identical clocks record different times - we do not have to bring them together to examine them (although that is one way) but we can continually interrogate the moving clock wrt to the ground clock

How do you "continually interrogate" one clock wrt the other if they are at different locations? Different inertial frames will have different definitions of simultaneity, and so will disagree about the relative rates of the clocks at different times. If you assume that the clocks obey Lorentz-symmetric laws of physics, then different inertial frames should be able to all use the same laws to predict how the clocks will behave (for example, each frame will predict a clock's ticking rate will be a function of its velocity in that frame), and they will all make the same prediction about what each clock reads when the two clocks reunite at a single location. Do you agree with this?

 

[yogi]

Jesse - we use the non rotating Earth centered reference system to interrogate GPS clocks all the time - we can calculate exactly what their daily drift is and correct them - if instead we do not preset a clock in satellite Earth orbit to compensate for the post launch orbital velocity - we can send a radio signal any time no matter where it is in its orbit and we will find it has a slower rate by the same amount relative to the tower clock - moveover, we can of course put different clocks at diffeent heights - e.g., we can arrange a launch platform at 100 milles up and a second at 200 miles above the Earth surface etc - and if both satellite clocks are synced respectivly to adjacent Earth tower clocks and launched into orbit at 100 miles and 200 miles respectivly, and no correction is made for the orbit velocity of either - when they are in orbit we can interrogate each of the two clocks from the tower at any point in their respective circular orbits. What will we find. The rate of each clock no matter where it is in its orbit, will be running uniformly slow with respect to the tower time - and each is slow by an factor that corresponds to its orbital velocity - i.e., each clock is running at its own uniform intrinsic rate at all times.

Now you can say that each clock runs at its own rate because of the invariance of the interval, or the difference in the space time path, or some other factor that is part of SR ...a lot of true statements - but not an explanation - what I would like to know is how do the two clocks in different orbits know at what rate to run relative to the Earth frame. Each clock has its own uniform intrinsic rate relative to the tower in accordance with their velocity relative thereto. - if that question doesn't bother you - so be it

 

[yogi]

Randall - i am astonised you would lecture on GR having never heard of the MTW - I got my first copy about 10 years ago - seemed like it was about $90 then - later a picked up a slightly used copy for $4 in the Escondido Library used book department - Of course having two copies doesn't make it easier to understand

 

[JesseM]

Jesse - we use the non rotating Earth centered reference system to interrogate GPS clocks all the time

How does that contradict my point? Once you make an arbitrary choice of which inertial reference frame you want to use, you can of course compare different clocks in that frame. But the choice is totally arbitrary, you could equally well have used some other inertial frame, and using the exact same laws you'd get all the same predictions about what clocks read when they meet, but different answers to how fast their respective rates are when they're apart. Do you disagree?

we can calculate exactly what their daily drift is and correct them - if instead we do not preset a clock in satellite Earth orbit to compensate for the post launch orbital velocity - we can send a radio signal any time no matter where it is in its orbit and we will find it has a slower rate by the same amount relative to the tower clock - moveover, we can of course put different clocks at diffeent heights - e.g., we can arrange a launch platform at 100 milles up and a second at 200 miles above the Earth surface etc - and if both satellite clocks are synced respectivly to adjacent Earth tower clocks and launched into orbit at 100 miles and 200 miles respectivly, and no correction is made for the orbit velocity of either - when they are in orbit we can interrogate each of the two clocks from the tower at any point in their respective circular orbits. What will we find. The rate of each clock no matter where it is in its orbit, will be running uniformly slow with respect to the tower time - and each is slow by an factor that corresponds to its orbital velocity - i.e., each clock is running at its own uniform intrinsic rate at all times.

Yes, and we could make similar corrections if we wanted to have the clocks be synchronized in an inertial frame moving at 0.99c relative to the earth, as opposed to the frame where the Earth's center is at rest. Do you disagree?

a lot of true statements - but not an explanation - what I would like to know is how do the two clocks in different orbits know at what rate to run relative to the Earth frame. Each clock has its own uniform intrinsic rate relative to the tower in accordance with their velocity relative thereto. - if that question doesn't bother you - so be it

The question doesn't bother me, but my answer is simple: the laws governing the clocks are known to have the mathematical property of Lorentz-invariance, which insures they must behave the same way in different inertial reference frames related to each other by the Lorentz transform. I've asked you several times whether you agree that given Lorentz-invariant laws, it is logically impossible that clocks would fail to behave as predicted by relativity or that they would not work the same way in different inertial reference frames, but you've never responded. Can you please do so now?

If you want to argue that the fundamental laws of nature might not be Lorentz-invariant, or that there has to be some conceptual reason they are all Lorentz-invariant, that's fine. But so far a lot of your arguments have seemed to take for granted that clocks follow known relativistic laws in some given frame (say, the frame where two clocks are initially at rest before one accelerates in your previous example), but then you question whether these situations could really be analyzed just as well from the point of view of another inertial frame. But this is a truly incoherent line of argument, because again, if you take for granted that clocks obey the known Lorentz-invariant laws in one inertial frame, then it's logically impossible that they would fail to obey the same laws in all other inertial frames.

 

[pervect]

Let me add my $.02.

If we have an inertial observer, and someone moving via a powered orbit in a circle around the observer, the two observers are always a constant distance apart.

Because they are a constant distance apart, the travel time for a light signal will always be constant, and everyone will agree that the observer traveling in a powered orbit has a clock that is ticking slower. Constant travel time makes direct comparison of the rates of clocks possible

The obserer in a powered orbit will not have a "frame" that covers all of space-time. However, he will have a local frame that includes the inertial observer.

The observer in the powered orbit will see the inertial observer's clock as ticking faster, due to "gravitational time dilation" in his local coordinate system, as the inertial observer will always be "above" him.

So, there isn't any ambiguity here - the inertial observer thinks the accelerating observer's clock is ticking slowly, and the accelerating observer thinks the inertial obserer's clock is ticking fast.

This is perfectly consistent with the simple idea that the clock following a geodesic in flat space-time is always the clock that experiences the most time.

 

[RandallB]

Randall - i am astonised you would lecture on GR having never heard of the MTW - I got my first copy about 10 years ago -

I’m not lecturing on GR I’m talking about SR. And is there some list of acronyms that we should all know so we don’t wise cracks from you guys about not knowing what MTW stands for here? Tens years working on getting SR is more astonishing than having to learn acronyms of others.
Do you have an acronym for your version of relativity; LR BR YR (Lorentz, Broken, Yogi) it sure isn’t SR.

And if you think your issues in this thread are GR, you’re wrong it’s SR where you’re still having problems. Until you understand SR, how can you hope to work from an understandable vocabulary with any mentor that’s not on the same page as you with what ever version of SR you’re using?

If you’re trying to learn the correct way to understand it. Stick with SR alone first. They won’t be able to help you in GR if you don’t have SR down first.

But, if your purpose is to convince someone of your view, do it in a SR environment; in GR you’ll never be able to communicate effectively if they don’t understand your version of SR. And be clear about your purpose if this is the case; at least be fair to the mentors that are only trying to help you see SR, if that is not your intent. I really don’t thing any are looking to pick up a new view of relativity, but some may be willing to look at your augments differently if you’re actually trying to bring forward a new view of relativity.
I honestly cannot tell which you are doing.

 

[RandallB]

No, I meant what I said. Check out for instance MTW's "Gravitation", pg 168, section $6.3 entitled "Constraints on the size of an accelerated frame".

I took a look at the book and yes the plots should cross as they do for SR frames, where one has been accelerated to a fixed higher speed. (The SR frame work, is the best to be working with yogi on, but if you think you can help him in a truly GR environment go ahead you have 100’s of posts to go)

The issue MTW are dealing with is an accelerating frame for the moving point. And yes those lines should not cross except that they should overlap as they do at t=0.

But why Kip has a problem with seeing an overlap at g-1 I don’t understand. By simply recognizing “simultaneity” (A simple SR issue) and applying it to this accelerating frame it is clear that the “time” at this distance is in the past for this “accelerating frame”. Therefore it has a time of t<0 where the speed and this line are the same and parallel with the original stating line for the point g-0 at t=0.
Thus the correct lines will obviously progress with curves to the left that go to some limit parallel to the original horizontal line off set up somewhat.

Likewise the lines to the right represent points at “future distances” and again by “simultaneity” rule those times will be in the future. Here the speeds are higher for the accelerating frame therefore the slope needs to be progressively steeper and curving the line forward. This Projects an expectation fitting with their other graphs. But they do repeat the concern of the g-1 point again. I’m just an independent non-pro but if I ever meet Kip again and have the chance maybe I’ll bring it up to him. I’m sure the book having been so long ago he’d be allowed some revisions to his old judgments.
RB

 

[yogi]

Jesse - Do i believe in Lorentz invarience - yes and no - how is that for a fence sitter. If you ask - do I believe in the invariance of the interval between two spacetime events in two different frames in relative uniform motion - the answer is yes until some experiment yet to be performed castrs doubt upon it - but there is no experiment that tests the transforms completely - when we take two space time points in two frames and derive the interval, the xv/c^2 term cancels - this has not been verified by experiment - so yes - I will withhold judgement at this point as to the universal validity of the transforms.

Is it always permissible to shift from the frame in which the clocks were syncronized to make interrogations of the orbiting clocks? I think not.
The satellite clocks will not be seen as running at a uniform rate in another frame in motion wrt to the non-rotating Earth centered reference frame.

 

[yogi]

pervect - your post 104 - I see no ambiguity either - don't know where you could have acquired the idea that i did - in fact it is what I have been trying to get across - earlier I drew an analogy to GR - the clock at the greater G potential runs faster - that clock at a lower potential runs slower - things are not reciprocal in GR nor are they in SR when only one clock has been accelerated into orbit

 

[yogi]

Randall - you are obviously going to have a difficult time undertanding the Gravity" book you borrowed - you are having a difficult time with my several statements to the effect that the resolution of the question doesn't involve anything but SR - first you accuse me of saying Relativity is Broken - title of another post - they you allege I am making a claim about GR - my reference to GR is strictly an analogy - nothing to do with it other than the fact that SR has in common with GR the fact that in some experiments things are not reciprocal.

 

[JesseM]

Jesse - Do i believe in Lorentz invarience - yes and no - how is that for a fence sitter.

I don't think you understand, yogi. "Lorentz-invariance" is just a mathematical property of certain equations, deciding whether or not a given equation shows Lorentz-invariance is as straightforward as deciding whether it's a polynomial.

Let's first consider the related concept of "Galilei-invariance", which is a bit simpler mathematically. The Galilei transform for transforming between different frames in Newtonian mechanics looks like this:

x&#039; = x - vt
y&#039; = y
z&#039; = z
t&#039; = t

and

x = x&#039; + vt&#039;
y = y&#039;
z = z&#039;
t = t&#039;

To say a certain physical equation is "Galilei-invariant" just means the form of the equation is unchanged if you make these substitutions. For example, suppose at time t you have a mass m_1 at position (x_1 , y_1 , z_1) and another mass m_2 at position (x_2 , y_2 , z_2 ) in your reference frame. Then the Newtonian equation for the gravitational force between them would be:

F = \frac{G m_1 m_2}{(x_1 - x_2 )^2 + (y_1 - y_2 )^2 + (z_1 - z_2 )^2}

Now, suppose we want to transform into a new coordinate system moving at velocity v along the x-axis of the first one. In this coordinate system, at time t' the mass m_1 has coordinates (x&#039;_1 , y&#039;_1 , z&#039;_1) and the mass m_2 has coordinates (x&#039;_2 , y&#039;_2 , z&#039;_2 ). Using the Galilei transformation, we can figure how the force would look in this new coordinate system, by substituting in x_1 = x&#039;_1 + v t&#039;, x_2 = x&#039;_2 + v t&#039;, y_1 = y&#039;_1, y_2 = y&#039;_2, and so forth. With these substitutions, the above equation becomes:

F = \frac{G m_1 m_2 }{(x&#039;_1 + vt&#039; - (x&#039;_2 + vt&#039;))^2 + (y&#039;_1 - y&#039;_2 )^2 + (z&#039;_1 - z&#039;_2 )^2}

and you can see that this simplifies to:

F = \frac{G m_1 m_2 }{(x&#039;_1 - x&#039;_2 )^2 + (y&#039;_1 - y&#039;_2 )^2 + (z&#039;_1 - z&#039;_2 )^2}

Comparing this with the original equation, you can see the equation has exactly the same form in the primed coordinate system as in the unprimed coordinate system. This is what it means to be "Galilei invariant". More generally, if you have any physical equation which computes some quantity (say, force) as a function of various space and time coordinates, like f(x,y,z,t) [of course it may have more than one of each coordinate, like the x_1 and x_2 above, and it may be a function of additional variables as well, like m_1 and m_2 above] then for this equation to be "Galilei invariant", it must satisfy:

f(x&#039;+vt&#039;,y&#039;,z&#039;,t&#039;) = f(x&#039;,y&#039;,z&#039;,t&#039;)

So in the same way, if we look at the Lorentz transform:

x&#039; = \gamma (x - vt)
y&#039; = y
z&#039; = z
t&#039; = \gamma (t - vx/c^2)
where \gamma = 1/\sqrt{1 - v^2/c^2}

and

x = \gamma (x&#039; + vt&#039;)
y = y&#039;
z = z&#039;
t = \gamma (t&#039; + vx&#039;/c^2)

Then all that is required for an equation to be "Lorentz-invariant" is that it satisfies:

f( \gamma (x&#039; + vt&#039; ), y&#039; , z&#039;, \gamma (t&#039; + vx&#039; /c^2 ) ) = f(x&#039; ,y&#039; ,z&#039; , t&#039;)

There may be some more sophisticated way of stating the meaning of Lorentz-invariance in terms of group theory or something, but if an equation is Lorentz-invariant, then it should certainly satisfy the condition above. Maxwell's laws of electromagnetism would satisfy it, for example. And it's pretty easy to see that if it satisfies this mathematical condition, then the equation must have the same form when you transform into a different inertial frame using the Lorentz transform. So this is enough to show beyond a shadow of a doubt that given Lorentz-invariant fundamental laws, all the fundamental laws must work the same in any inertial reference frame, and if you know the equation for a given law as expressed in some particular inertial frame (the rest frame of the center of the earth, for example) then it is a straightforward mathematical question as to whether or not this equation is Lorentz-invariant, it's not an experimental issue (the only experimental issue is whether that equation makes correct predictions in the first place). Do you disagree with any of this?

Is it always permissible to shift from the frame in which the clocks were syncronized to make interrogations of the orbiting clocks? I think not.

The satellite clocks will not be seen as running at a uniform rate in another frame in motion wrt to the non-rotating Earth centered reference frame.

Uh, why does this mean it's not "permissible" to shift into another frame? That's the whole point, that different frames disagree about whether a given set of clocks is running at a uniform rate. But all frames will agree on all physical questions like what two clocks will read at the moment they meet at a single location in space. You need to define what you mean by "permissible", when physicists use this term all it means is that you can use the same laws of physics in another frame and all your predictions about physical questions will still be accurate (that's why it's not 'permissible' to use the ordinary rules of SR for inertial frames in a non-inertial coordinate systems, because you would make wrong predictions if you did this). Given Lorentz-invariant laws, this is automatically going to be true for all inertial frames.

Also, the GPS clocks are programmed to adjust themselves so that they tick at a constant rate in the frame of the earth. My other point was that this is a completely arbitrary choice made by the designers, you could just as well design the orbiting GPS clocks to adjust themselves so that they tick at a constant rate in the frame of an inertial observer moving at 0.99c relative to the earth. Would you then say it is not "permissible" to analyze these clocks in the rest frame of the earth, since they would not be running at a uniform rate in the Earth's frame?

 

[pervect]

pervect - your post 104 - I see no ambiguity either - don't know where you could have acquired the idea that i did - in fact it is what I have been trying to get across - earlier I drew an analogy to GR - the clock at the greater G potential runs faster - that clock at a lower potential runs slower - things are not reciprocal in GR nor are they in SR when only one clock has been accelerated into orbit

Fine with me. Actually I think I need to tighten this up a little bit. The round trip time for light signals between two obserers is something that can be measured - A sends a signal #1 to B, B sends a signal #2 to A on recipt of A's signal. A measures the interval on his clock between the sending of the signal #1 and the receiving of signal #2 as the "round-trip time".

If this round-trip time is always constant, we can always compare the rate of two clocks unambiguously.

We may need to demand that the round-trip time is constant for both A and B before we can compare rates, but I think it is true that if A's round trip time is constant, so is B's. I'm relying on my intuition a bit here, though.

Of course A and B don't necessarily have to agree on the value of the round-trip time (and in general they won't) - they just have to agree that it's constant.

 

[Hurkyl]

but there is no experiment that tests the transforms completely

The transforms are mathematical things, not physical things -- there cannot be an experiment that tests them at all.

 

[RandallB]

The satellite clocks will not be seen as running at a uniform rate in another frame in motion wrt to the non-rotating Earth centered reference frame.

This statement alone stands as a claim the Einstein’s version of relativity is broken so quit complaining.

What I’d wish you’d do tell us what your trying to do in your posts, they seem to flip from one objective to a the other.
Are you:
A) trying to convince others that the standard view of SR (and extending into GR as well) is somehow wrong or incomplete. And your 'LR-like' view or something else must be better.
OR
B) sincerely trying to learn SR completely, to filling the gaps of information about it, that leave you unable to see concepts in books you’ve had for 10 years.

For the sake of all those that are trying to respond to you, be clear on this; are you arguing a point of view; or trying to learn something. And please refrain on saying “yes & no” or “both”, do one or the other.

 

[yogi]

I have no agenda Randall - my interest in SR goes back many years - likely before you were born - I pose questions that come to mind - if those questions lead to a different view ...one I have overlooked - great. Usually what happens on these boards is an attack - either I don't understand it or I am not qualified to question it - but for a few posters, the attitude is always one of condesention.

 

[yogi]

If anyone thinks it is easy to synchronize GPS satellite clocks in some frame than the non-rotating Earth centered system -I would like to see how you would go about doing it.

 

[yogi]

Hurkyl - The transforms relate time and distances - they are not abstract mathematical artifact - these are physical things - my point is with you and Jesse - the mathematical relationships (LT) have been confirmed in certain experiments - but those experiments do not test the fundamental premise upon which Einstein's derivation was based - perhaps w/o complete justification, I do have a stong conviction that the spacetime interval is invarient.

 

[yogi]

pervect - i would agree that any interrogation must depend upon the constancy of the round trip time - and since the GPS clock will always be found to be running at a uniform rate relative to the ground station - we have a convincing demonstration of the constancy of c - at least in the Earth centered frame

 

[yogi]

Jesse - your post 110 - last Paragraph: Transforming to another frame - what I have been trying to discuss was the non reciprocal reality of time dilation in certain experiments - if we have a GPS clock that was originally at the top of the tower and launched into orbit from there with no velocity correction - we have a situation where the ground clocks run consistently fast wrt to the GPS satellite clock and the GPS satellite clock always runs slow wrt to the ground clocks and we can verify this non symmetrical situation by interrogating the GPS clock with radio signals - that is the experiment. To inquire as to transforming to a frame in high speed motion wrt to the Earth simply subverts the objective. Such a transformation of course is possible, but you have missed the whole point -we are now back in a situation where whatever is measured is apparent - the two frames have not been synchronized - Einstein only makes a prediction about real time dilation when one of two originally synchronized clocks is accelerated to a uniform velocity wrt the other. This is the subject of the thread - which i would like to explore further.

 

[JesseM]

If anyone thinks it is easy to synchronize GPS satellite clocks in some frame than the non-rotating Earth centered system -I would like to see how you would go about doing it.

If the satellites can figure out their velocity relative to the center-of-earth frame and adjust their clock rates accordingly, it is trivial to figure out their velocity relative to any other inertial frame and adjust their clock rates to be constant in that frame instead. Do you doubt that if I know my velocity in Earth's frame and I know the Earth's velocity in frame X, I can easily figure out my velocity in frame X, and from this figure out how much my clocks would be slowed down in frame X?

 

[JesseM]

Jesse - your post 110 - last Paragraph: Transforming to another frame - what I have been trying to discuss was the non reciprocal reality of time dilation in certain experiments

More ill-defined terminology...what does "non-reciprocal" mean in yogi-speak? Surely you don't mean "non-reciprocal in the way the laws of physics work in different frames", do you? Please address the main part of post 110 and not the last paragraph, where I explained that "Lorentz-invariance" is simply a mathematical property of certain equations, and that given laws of physics whose equations in our own inertial frame have this property, it is automatically going to be true that the laws of physics will obey the same equations in all other inertial frames. Do you deny this or not?

if we have a GPS clock that was originally at the top of the tower and launched into orbit from there with no velocity correction - we have a situation where the ground clocks run consistently fast wrt to the GPS satellite clock and the GPS satellite clock always runs slow wrt to the ground clocks and we can verify this non symmetrical situation by interrogating the GPS clock with radio signals - that is the experiment.

It is symmetric in how the laws of physics work in different inertial frames, which is all that most physicists would mean by "symmetric" in the context of special relativity. If you have your own idiosyncratic definition of "symmetrical", please present it.

Do you agree that if the GPS clock is orbiting the Earth at a constant speed in the center-of-the-earth frame, that means that in other inertial frames the speed of the GPS clock is not constant? (This would be just as true in Newtonian mechanics as in relativity, of course.) Do you agree that if each inertial frame assumes the same relationship between instantaneous speed in that frame and instantaneous rate of ticking (ie that if the clock is moving at speed v in that frame it will be slowed down by a factor of \sqrt{1 - v^2/c^2}), then different inertial frames will disagree about the relative rate of the tower clock and the orbiting clock at a given moment (with 'given moment' meaning something different in different frames too, due to different definitions of simultaneity), yet they will all make the same prediction about how far behind the orbiting clock will be at the moment it completes an orbit and reunites with the tower clock at a single point in space? Please, please give me direct answers to this question, when I ask you questions in my posts they are not meant to be rhetorical, and it's incredibly frustrating when I ask you questions that I hope will help pin down your nebulous comments and you just ignore them and comment on a single statement in my post.

To inquire as to transforming to a frame in high speed motion wrt to the Earth simply subverts the objective. Such a transformation of course is possible, but you have missed the whole point -we are now back in a situation where whatever is measured is apparent - the two frames have not been synchronized - Einstein only makes a prediction about real time dilation when one of two originally synchronized clocks is accelerated to a uniform velocity wrt the other. This is the subject of the thread - which i would like to explore further.

There could only be a "real time dilation" in the sense that all frames would agree on how much time elapsed on two clocks between two points in time in a case where the clocks started at the same location and ended at the same location. Einstein would certainly never say that in a case where two clocks started at separate locations and then one accelerated towards another, there is any "real" (frame-independent) truth about which clock was ticking faster or slower. Different frames would disagree about this, and there is no physical reason to prefer one frame's analysis to another. If you disagree with this, then it's important that we first see if you agree with my statements above that any laws of physics which have the mathematical property of Lorentz-invariance will automatically work the same way in all different frames, and whether you also agree that all frames will make the same prediction about all physical questions like what two clocks will read at a moment when they are at a single location in space. If you don't agree with this, then you're expressing some basic ignorance about purely mathematical issues in relativity which needs to be corrected. If you do agree with this, yet still feel that there is some other reason to "prefer" one frame's analysis of the situation to another's, you need to explain what sort of aesthetic criteria you are using here to prefer one over the other despite the fact that all will see the same laws of physics and make the same physical predictions. And if you also want to continue to defend the absurd proposition that Einstein would agree with you about preferring one frame's analysis over another's, you need to provide the quotes that you think support this interpretation.