- #1
sphyrch
- 35
- 9
Currently reading Einstein's booklet on SR and GR. At this point SR has been explained but GR hasn't been introduced yet.
The setup is like this: ##A## is present in an inertial reference frame and looking down on a flat rotating disc. ##B## is sitting on the edge of that disc, ##C## is sitting somewhere on the radius connecting the disc's center ##O## and ##B##. Suppose ##B##, ##C## and ##O## each have an identically-constructed clock. From ##A##'s PoV, ##C##'s clock will tick at a slower rate since ##C## has some velocity w.r.t. ##A##. Then it's written that ##O## will obviously see the same slowdown for ##C##'s clock w.r.t. his own clock. This makes sense to me since ##O## isn't actually moving w.r.t. ##A##, so effectively ##O## belongs to ##A##'s reference frame.
Visually I'm seeing it like this:
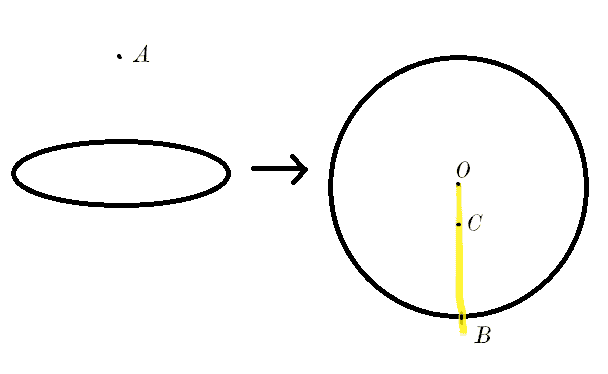
##A## looks down on the 2D disc. But ##C## and ##B## can only see along one dimension, which is the radius ##OCB## (and that radius extending both ways indefinitely). ##C## and ##B## consider themselves to be at rest. My question is: can ##C## also conclude that ##B##'s clock is ticking slower than his (only using SR-based arguments, since GR hasn't been introduced yet in the text) ?
If ##C## had visibility beyond the single direction I've highlighted in yellow, then I understand he'd be able to somehow measure ##B##'s velocity w.r.t. himself, observe that that velocity is non-zero and hence say that "by SR, ##B##'s clock ticks at a slower rate". But what if ##C## can't see beyond the single yellow-highlighted dimension? Is the only way for him to reach that conclusion is to just watch ##C##'s clock tick rate (as he can't theoretically deduce it)?
The setup is like this: ##A## is present in an inertial reference frame and looking down on a flat rotating disc. ##B## is sitting on the edge of that disc, ##C## is sitting somewhere on the radius connecting the disc's center ##O## and ##B##. Suppose ##B##, ##C## and ##O## each have an identically-constructed clock. From ##A##'s PoV, ##C##'s clock will tick at a slower rate since ##C## has some velocity w.r.t. ##A##. Then it's written that ##O## will obviously see the same slowdown for ##C##'s clock w.r.t. his own clock. This makes sense to me since ##O## isn't actually moving w.r.t. ##A##, so effectively ##O## belongs to ##A##'s reference frame.
Visually I'm seeing it like this:
##A## looks down on the 2D disc. But ##C## and ##B## can only see along one dimension, which is the radius ##OCB## (and that radius extending both ways indefinitely). ##C## and ##B## consider themselves to be at rest. My question is: can ##C## also conclude that ##B##'s clock is ticking slower than his (only using SR-based arguments, since GR hasn't been introduced yet in the text) ?
If ##C## had visibility beyond the single direction I've highlighted in yellow, then I understand he'd be able to somehow measure ##B##'s velocity w.r.t. himself, observe that that velocity is non-zero and hence say that "by SR, ##B##'s clock ticks at a slower rate". But what if ##C## can't see beyond the single yellow-highlighted dimension? Is the only way for him to reach that conclusion is to just watch ##C##'s clock tick rate (as he can't theoretically deduce it)?