- #1
- 3,488
- 257
Homework Statement
This is problem 2.9 from Kleppner and Kolenkow, 2nd edition. I think I got it right, just want to check since I'm self-studying.
Masses on table
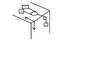
Two masses, ##A## and ##B##, lie on a frictionless table, as shown (see my crudely drawn figure in the thumbnail
). They are attached to either end of a light rope of length ##l## which passes around a pulley of negligible mass. The pulley is attached to a rope connected to a hanging mass, ##C##. Find the acceleration of each mass.Homework Equations
##F = ma##
The Attempt at a Solution
First, I chose the coordinates as follows:
* ##x## points horizontally, away from and perpendicular to the table edge
* ##y## points downward vertically
Define the positions of the objects:
* ##x_A## = horizontal position of mass ##A##
* ##x_B## = horizontal position of mass ##B##
* ##x_p## = horizontal position of movable pulley (the one to the left in the figure)
* ##y_C## = vertical position of mass ##C##
* Note that I didn't draw it very well, but the pulley to the right in the figure is fixed: it is attached rigidly to the table.
I obtained the following constraints due to the rope connections:
$$2 \ddot x_p = \ddot x_A + \ddot x_B$$
$$\ddot x_p + \ddot y_C = 0$$
Combining these, we get
$$-2 \ddot y_C = \ddot x_A + \ddot x_B$$
I then considered the forces on each mass, and on the movable pulley. Masses ##A## and ##B## each have tension ##T_1## pointing to the right (negative ##x##) due to the rope. Thus,
$$T_1 = -M_B \ddot x_B = -M_A \ddot x_A$$
Mass ##C## is acted upon by gravity downward and by tension from the second rope upward. This gives us
$$M_C g - T_2 = M_C \ddot y_C$$
The two tensions are related by the movable pulley: tension ##T_2## pulls to the right, and ##2T_1## pulls to the left. Since the pulley is massless, this gives us ##T_2 = 2T_1##.
Thus we have five equations and five unknowns. I won't go through all the algebra as it's rather ugly but routine. My answer, in case anyone has done this problem and has their solutions available to verify, is:
$$\ddot x_A = \frac{-2 M_C M_B g}{M_C M_B + M_C M_A + 4 M_B M_A}$$
$$\ddot x_B = \frac{M_A}{M_B} \ddot x_A = \frac{-2 M_C M_A g}{M_C M_B + M_C M_A + 4 M_B M_A}$$
$$\ddot y_C = -\frac{1}{2}(\ddot x_A + \ddot x_B) = \frac{(M_C M_A + M_C M_B)g}{M_C M_B + M_C M_A + 4 M_B M_A}$$
I checked several special cases:
Case 1 : ##M_C = 0##. In this case, all the accelerations are zero, as expected since nothing is pulling the system.
Case 2 : ##M_A = 0##. In this case, ##\ddot x_B = 0## (intuitively expected because the "path of least resistance" is to pull massless mass ##A## and leave mass ##B## alone), ##\ddot x_C = (M_C M_B g)/(M_C M_B) = g## (reasonable because ##C## is able to free-fall), and ##\ddot x_A = -2 (M_C M_B g) / (M_C M_B) = -2g## (reasonable since ##C## is free-falling and the movable pulley doubles the motion of ##A##).
Case 3 ##M_A = M_B = M_C##. Here the expressions reduce to ##\ddot x_A = \ddot x_B = -g/3## and ##\ddot x_C = g/3##. I guess this makes sense because gravity's force gets distributed across the three masses equally, so the acceleration of each one is one third of ##g##. I think.
Case 4 ##M_A = M_B = 0##. Here the expressions are invalid because the denominators are zero. But if we step back to the earlier equations, we get: ##T_1 = 0##, ##M_c g = M_C \ddot y_C##, hence ##\ddot y_C = g## as expected since ##C## can free-fall. Also, ##\ddot x_A + \ddot x_B = -2g## and ##\ddot x_A = \ddot x_B##, which forces ##\ddot x_A = \ddot x_B = -g##, as expected since they simply follow ##C## down.
Attachments
Last edited:
