Lagrange equations: Two blocks and a string

[Zamarripa]

Homework Statement

Two blocks, each of mass M, are connected by an extensionless, uniform string of length l. One block is placed on a smooth horizontal surface, and the other block hangs over the side, the string passing over a frictionless pulley. Describe the motion of the system in two cases, first when the mass of the string is negligible, and second when the string has a mass m.

Relevant Equations

$$T_{string}=\frac{1}{2}m\dot{y} $$

I've problems understanding why the kinetic energy of the string is only

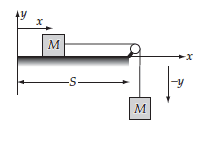
$$T_{string}=\frac{1}{2}m\dot{y} $$

Why the contribution of the string in the horizontal line isn't considered?

 

[PeroK]

What's the formula for KE?

 

[Zamarripa]

What's the formula for KE?

$$T=\frac{1}{2}mv^2$$

 

[PeroK]

$$T=\frac{1}{2}mv^2$$

Which is not what you're using?

 

[Zamarripa]

Yes, but what about the contribution on the horizontal?

 

[PeroK]

Yes, but what about the contribution on the horizontal?

What contribution from the horizontal?

The problem is that you have $\frac 1 2 m \dot y$ instead of $\frac 1 2 m \dot y^2$.

 

[Zamarripa]

What contribution from the horizontal?

The problem is that you have $\frac 1 2 m \dot y$ instead of $\frac 1 2 m \dot y^2$.

The string at the horizontal is also moving

 

[PeroK]

The string at the horizontal is also moving

So, what do you think the KE of the string should be?

 

[Zamarripa]

So, what do you think the KE of the string should be?

$$\frac{1}{2}m\frac{(s-x)}{l}\dot{x}$$

where $m\frac{(s-x)}{l}$ is the mass of the string in the horizontal

 

[PeroK]

$$\frac{1}{2}m\frac{(s-x)}{l}\dot{x}$$

where $m\frac{(s-x)}{l}$ is the mass of the string in the horizontal

1) The whole string is moving, so you need the whole mass of the string: $m$.

2) $\dot x = \dot y$, as the string is inextensible.

3) You need to use $v^2 = \dot x^2 = \dot y^2$ for KE. You can't use $\dot x$ or $\dot y$.