Lagrangian function of pendulum

[Grand]

Homework Statement

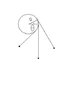
Find the Lagrangian and the Lagrangian equations for this pendulum (see the picture). Radius of circle is a, mass of the bob is m and l is the length of the pendulum when it hangs straight down.

Homework Equations

The Attempt at a Solution

I obtain:
L=\frac{1}{2}m(a^2\dot{\theta}^2+(l+a\theta)^2\dot{\theta}^2)-mg(a\sin\theta-(l+a\theta)\cos\theta)
while the answer in the book misses the term a^2\dot{\theta}^2 - where have I gone wrong?
Thank you in advance.

 

[ehild]

How did you get that extra term? The x,y coordinates of the bob with respect to the centre of the circle are x=a cos(θ)+(l+a)sin(θ), y=sin(θ)-(l+a)cos(θ). Take the time derivatives to get the x, y components of velocity.

ehild