Oomph!
- 55
- 0
Hello. I have some problems with making Lagrangian. I need your advice.
1. Homework Statement
I have this situation:
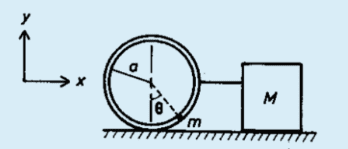
Consider the circular path is intangible and without friction. I have to find Lagrangian for coordinates x and θ.
[/B]
L = U - V
I know the result from a book:

The origin of the coordinate system is at the center of the initial position of the circular trajectory.
I understand that the fist part is kinetic energy of big cube of mass M in coordinate x.The second part is kinetic energy of bead of mass m in a circle in coordinate x.
I don't understand to third part. I think that the m (mass of bead) is missing there. If I will consider that m is there, it is kinetic energy of bead in coordinate θ.
What is the poind of fourth part? I don't see it.
The last part is potentional energy of bead, I understand.
I wrote it there:

So, could you tell me, if this Lagrangian right? And if it is not, how it has to look?
Thank you.
1. Homework Statement
I have this situation:
Consider the circular path is intangible and without friction. I have to find Lagrangian for coordinates x and θ.
Homework Equations
[/B]
L = U - V
The Attempt at a Solution
I know the result from a book:
The origin of the coordinate system is at the center of the initial position of the circular trajectory.
I understand that the fist part is kinetic energy of big cube of mass M in coordinate x.The second part is kinetic energy of bead of mass m in a circle in coordinate x.
I don't understand to third part. I think that the m (mass of bead) is missing there. If I will consider that m is there, it is kinetic energy of bead in coordinate θ.
What is the poind of fourth part? I don't see it.
The last part is potentional energy of bead, I understand.
I wrote it there:
So, could you tell me, if this Lagrangian right? And if it is not, how it has to look?
Thank you.