Willem_lift
- 2
- 0
Hello all,
This is the situation: a pipe, shown in de drawing below, is lifted at a constant speed of 1m/min. The pipe is closed at the top and open at the bottom. For obvious reasons, a ventilation hole is required at the top. The intention is to lift a minimum amount of water, in other words, the height difference of the water inside the pipe and the sea level should be minimal.
Some more info:
-pipe diameter at top: 1.3 meter
-pipe diameter at bottom: 2.6 meter
I tried some things to calculate the required vent hole area, but I'm not sure if I did it right at all. Hope you can help me!
This is how I did it:
I determined that an height difference of 0.5 m was allowable. 0.5 m of water results in a pressure of P = 0.5*g*rho_saltwater = 0.5*9.81*1028 = 5042.3 N/m^2
Then I used an online calculator:
http://www.tlv.com/global/TI/calculator/air-flow-rate-through-orifice.html
And filled in the following variables:
-Air temperature: 10 degrees Celsius
-Primary pressure: 5042.34 Pa
-Secondary pressure: 0 Pa
For the volumetric flow I used the most unfavorable situation, which is when the pipe is almost out of the water. At that point the largest amount of water leaves the pipe.
Q = r^2*pi*lifting_speed = (2.6/2)^2 * 3.14 * 1 = 5.3 m^3/min
Then iterate the tool till you find an appropriate vent hole area. I found that an hole with a diameter of 50mm would do the job.
Is this in any way correct? And I would like to be able to calculate it myself, instead of using a tool. Anybody know how to?
Thanks in advance!
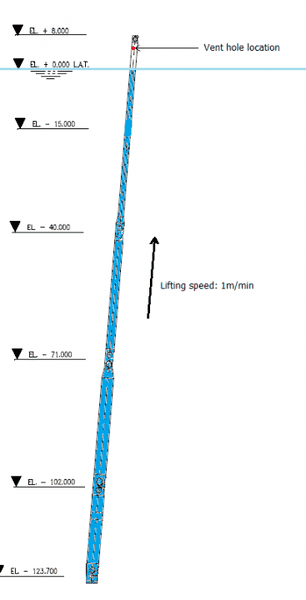
This is the situation: a pipe, shown in de drawing below, is lifted at a constant speed of 1m/min. The pipe is closed at the top and open at the bottom. For obvious reasons, a ventilation hole is required at the top. The intention is to lift a minimum amount of water, in other words, the height difference of the water inside the pipe and the sea level should be minimal.
Some more info:
-pipe diameter at top: 1.3 meter
-pipe diameter at bottom: 2.6 meter
I tried some things to calculate the required vent hole area, but I'm not sure if I did it right at all. Hope you can help me!
This is how I did it:
I determined that an height difference of 0.5 m was allowable. 0.5 m of water results in a pressure of P = 0.5*g*rho_saltwater = 0.5*9.81*1028 = 5042.3 N/m^2
Then I used an online calculator:
http://www.tlv.com/global/TI/calculator/air-flow-rate-through-orifice.html
And filled in the following variables:
-Air temperature: 10 degrees Celsius
-Primary pressure: 5042.34 Pa
-Secondary pressure: 0 Pa
For the volumetric flow I used the most unfavorable situation, which is when the pipe is almost out of the water. At that point the largest amount of water leaves the pipe.
Q = r^2*pi*lifting_speed = (2.6/2)^2 * 3.14 * 1 = 5.3 m^3/min
Then iterate the tool till you find an appropriate vent hole area. I found that an hole with a diameter of 50mm would do the job.
Is this in any way correct? And I would like to be able to calculate it myself, instead of using a tool. Anybody know how to?
Thanks in advance!