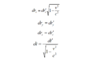LT & Translation Symmetry: Problem Analysis

[HaoBoJiang]

TL;DR Summary

Does Lorentz transformation have the symmetry of time and space translation? Why?

As we all know, for the reference frame S' and S of relative motion, according to Lorentz transformation, we can get

As we all know, for the reference frame S' and S of relative motion, according to Lorentz transformation, we can get​

As we all know, for the reference frame S' and S of relative motion, according to Lorentz transformation, we can get

 

[PeterDonis]

@HaoBoJiang first of all, please use the PF LaTeX feature to post equations:

https://www.physicsforums.com/help/latexhelp/

We do not allow equations posted as images, since they cannot be quoted in replies.

Second, the transformations you are calling "Lorentz transformations" are different transformations from space and time translations. The transformations you are calling "Lorentz transformations" are more precisely called "boosts". Boosts are not translations, so of course you should not expect them to have the properties of translations.

The full group of Lorentz transformations contains boosts and spatial rotations, but not translations. If you add space and time translations, you get a larger group called the Poincare group.

 

[Orodruin]

Second, the transformations you are calling "Lorentz transformations" are different transformations from space and time translations. The transformations you are calling "Lorentz transformations" are more precisely called "boosts". Boosts are not translations, so of course you should not expect them to have the properties of translations.

I don’t know if I would say that he quoted boosts. It looks as if he has just quoted length contraction and time dilation.

 

[PeterDonis]

I don’t know if I would say that he quoted boosts. It looks as if he has just quoted length contraction and time dilation.

Yes, you're right, the actual equations given in the OP are not the full Lorentz transformation (boost) equations.

 

[vanhees71]

The full symmetry group of Minkowski space as an affine pseudo-Euclidean space is the group $\text{ISO}(1,3)^{\uparrow}$, i.e., the proper orthochronous Poincare group (I leave out the non-continuously connected parts, including time reversal and space reflections). They are the semidirect product of the proper orthochronous Lorentz group, represented by $\mathrm{R}^{4 \times 4}$ matrices, ${\Lambda^{\mu}}_{\nu}$ fulfilling
$$\eta_{\mu \nu} {\Lambda^{\mu}}_{\rho} {\Lambda^{\nu}}_{\sigma} =\eta_{\rho
\sigma}, \quad \mathrm{det} \hat{\Lambda}=+1, \quad {\Lambda^0}_{0} \geq 1.$$
with the pseudo-metric components $(\eta_{\mu \nu})=\mathrm{diag}(1,-1,-1,-1)$, and translations $x^{\mu} \rightarrow x^{\mu}+a^{\mu}$ with $a^{\mu}=\text{const}.$

The group element is $(\hat{\Lambda},a)$, acting on the spacetime components as
$$(\hat{\Lambda}, a) \boldsymbol{x}=\hat{\Lambda} \boldsymbol{x} +a.$$
The group product thus is given by
$$(\hat{\Lambda}_2,a_2)(\hat{\Lambda}_1,a_1)=(\hat{\Lambda}_2 \hat{\Lambda}_1,a_2+\hat{\Lambda}_2 a_1).$$