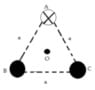
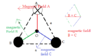
At point ## O ##, the magnetic field from ## A ## does not cancel the magnetic field from ## B ##, nor does it cancel the magnetic field from ## C ##. ## \\ ## It may seem logical to do this, but it is incorrect to think of the magnetic field at ## O ## from anyone of ## A##, ## B ##, or ## C ## as being clockwise or anticlockwise. The magnetic fields around a given wire of current are clockwise or anti-clockwise, but when looking at a point ## O ##, the magnetic field from anyone of ## A ##, ## B ##, or ## C ## is a vector that points in a given direction in the x-y plane, rather than clockwise or anti-clockwise. ## \\ ## There is a shortcut solution that I presented in the first line or two of post 16, which I will describe in more detail here: If the currents are all in the same direction (e.g. out of the paper) from the three wires, by symmetry the magnetic fields from them will cancel at ## O ##. This is because if there were a non-zero component at ## O ## from this symmetric configuration, it would need to also point in the two other directions (120 degrees apart) by symmetry. Thereby, three wires with currents in the same direction gives the result of zero for the magnetic field at ## O ##. (And then the current from wire ## A ##, which is one unit of current into the paper, can be considered to be composed of one unit of current out of the paper, along with two units into the paper). ## \\ ## The magnetic field at ## O ## from the two units of current into the paper at ## A ## is then the only thing that needs to be computed to get the answer to the total magnetic field at ## O ## from the currents in the three wires for the problem as it is given.