vaxopy
- 26
- 0
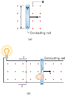
Suppose the light bulb in Figure 22.4b is a 60.0-W bulb with a resistance of 240 W. The magnetic field has a magnitude of 0.40 T, and the length of the rod is 0.60 m. The only resistance in the circuit is that due to the bulb. Minimally, how long would the rails on which the moving rod slides have to be, in order that the bulb can remain lit for one-half second?
Anyone know how i can start going about solving this :)?
Anyone know how i can start going about solving this :)?