likephysics
- 638
- 4
π²³ ∞ ° → ~ µ ρ σ τ ω ∑ … √ ∫ ≤ ≥ ± ∃ · θ φ ψ Ω α β γ δ ∂ ∆ ∇ ε λ Λ Γ ô
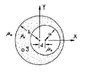
An arbitrarily long hallow cylindrical electric conductor shown carries a static electric current density J=\hat{z}J0. Determine the magnetic flux density B in the hallow region of radius a. Your result should show that B is constant in this region.
∫B.dl = µ0I
current I = \hat{z}J0pi(b2-a2)
B. 2pia = µ0 \hat{z}J0pi(b2-a2)
B = µ0 \hat{z}J0(b2-a2) /2a
I am not sure about B.dl being B.2pi a
Homework Statement
An arbitrarily long hallow cylindrical electric conductor shown carries a static electric current density J=\hat{z}J0. Determine the magnetic flux density B in the hallow region of radius a. Your result should show that B is constant in this region.
Homework Equations
∫B.dl = µ0I
The Attempt at a Solution
current I = \hat{z}J0pi(b2-a2)
B. 2pia = µ0 \hat{z}J0pi(b2-a2)
B = µ0 \hat{z}J0(b2-a2) /2a
I am not sure about B.dl being B.2pi a
Attachments
Last edited: