Magnetic flux is the same if we apply the Biot Savart?

[mertcan]

Hi, initially I am aware that magnetic flux is conserved due to divergence of magnetic field is zero and for long solenoid, magnetic field inside is uniform. So magnetic field intensity (B) at point P,Q,S, T,R,U(in the attachment) must be same. But my question is : can we obtain the same magnetic field intensity at point S or R again at the point P or U using biot savart rule for constant current? I am asking because it seems to me that for instance if we apply biot savart at point S then we will obtain different magnetic field intensity from point U applying biot savart again( because point U is far away from current loops but point S is closer to current loops...)

 

[berkeman]

View attachment 212470
Hi, initially I am aware that magnetic flux is conserved due to divergence of magnetic field is zero and for long solenoid, magnetic field inside is uniform. So magnetic field intensity (B) at point P,Q,S, T,R,U(in the attachment) must be same. But my question is : can we obtain the same magnetic field intensity at point S or R again at the point P or U using biot savart rule for constant current? I am asking because it seems to me that for instance if we apply biot savart at point S then we will obtain different magnetic field intensity from point U applying biot savart again( because point U is far away from current loops but point S is closer to current loops...)

Are you familiar yet with the difference between Magnetizing Inductance Lm and Leakage Inductance Lk?

 

[mertcan]

Are you familiar yet with the difference between Magnetizing Inductance Lm and Leakage Inductance Lk?

Thank you for your return @berkeman
Yes, I am familiar with those notions( I am aware magnetic flux lines may not be conserved 100 percent, iron core is being used to maximize that flux). But I wonder that without using conservation of flux can we obtain the same similar result just using biot savart rule in order to find magnetic field intensity for point P and U?

 

[Charles Link]

In applying Biot-Savart, you also need to apply it to the magnetic surface currents from the magnetized iron. This problem with the air-gap is somewhat unique and the equation $\oint H \cdot dl=N I$ is used. Let me give you a "link" to this problem which previously appeared on Physics Forums: (need to look for it=should have it momentarily=here it is: https://www.physicsforums.com/threads/absolute-value-of-magnetization.915111/ See also the "link" in post #2 of this "link" that has the Feynman lectures derivation of it. $\\$ For a problem that treats the magnetic surface currents, see https://www.physicsforums.com/threads/magnetic-field-of-a-ferromagnetic-cylinder.863066/

 

[Charles Link]

@mertcan Please see the edited post above: I found the "links" I was looking for.

 

[mertcan]

thanks @Charles Link for your effort, but @berkeman I also would like to see your return to obtain different comments...

 

[Charles Link]

Just an additional comment or two: The equation $\oint H \cdot \, dl =NI$ is quite exact, but the solution of this involves a couple of approximations based on the fact that because $\nabla \cdot B=0$ that the lines of flux of $B$ are conserved. Thereby, especially for a small gap, the assumption is made that $H$ takes on two values: $H_1$ in the magnetized material and $H_2$ in the gap. This assumption that $H_1$ is constant for the material, essentially assumes that $M$ is also constant in the material, because $B$ is assumed to be continuous and constant, and that $M$ takes on a value given by $M=\chi_m H_1$. The magnetic surface currents from this magnetization, along with the $B$ from the current in the windings, can be computed from Biot-Savart for a cylindrical geometry. For this rectangular geometry, any Biot-Savart calculations are much less precise, and the assumptions above are normally used to solve the problem.

 

[vanhees71]

You can treat everything, i.e., magnetic fields from currents as well as those from magnetizations (ferromagnets) by using (in Heaviside Lorentz units):
$$\vec{j}_{\text{tot}}=\vec{j}_{\text{charges}}+\underbrace{c \vec{\nabla} \times \vec{M}}_{\vec{j}_\text{mag}}.$$
Note that at a surface of a ferromagnet this implies a surface-magnetization current.

 

[mertcan]

@Charles Link While I was reviewing your answers above, I saw you mentioned the surface currents, and I deem that if surface currents exist then time varied magnetic field must exist. BUT my question is: when we have NO time varied magnetic field ( no time varied current), magnetic field intensity (B) at point P,Q,S, T,R,U still be same BUT now it is easy to apply biot-savart rule because no surface currents exist and if we apply biot-savart I do not deem that magnetic field intensity (B) at point P,Q,S, T,R,U be same because of distance difference between points? What can you say about that situation??

 

[Charles Link]

@Charles Link While I was reviewing your answers above, I saw you mentioned the surface currents, and I deem that if surface currents exist then time varied magnetic field must exist. BUT my question is: when we have NO time varied magnetic field ( no time varied current), magnetic field intensity (B) at point P,Q,S, T,R,U still be same BUT now it is easy to apply biot-savart rule because no surface currents exist and if we apply biot-savart I do not deem that magnetic field intensity (B) at point P,Q,S, T,R,U be same because of distance difference between points? What can you say about that situation??

The magnetic surface currents are present even in the static case, and occur also in a permanent magnet. The magnetic field for any magnet can be computed from Biot-Savart (or Ampere's law) if the magnetization $\vec{M}$ is known, so that the surface currents can be computed. (In complete detail, the magnetic current density $\vec{J}_m=\frac{\nabla \times \vec{M}}{\mu_o}$. The result is that there are surface currents at boundaries given by surface current per unit length $\vec{K}_m=\frac{\vec{M} \times \hat{n}}{\mu_o}$, but there can also be magnetic current densities in the bulk material in regions of non-uniform $\vec{M}$). $\\$ For a somewhat detailed example of the magnetic surface currents, see https://www.physicsforums.com/threads/magnetic-field-of-a-ferromagnetic-cylinder.863066/

 

[Charles Link]

And just one additional comment: If you do attempt a mathematical solution of this magnetic core with a gap problem using a model that assumes a linear response of the material so that you can write $M=\mu_o \chi_m H= \chi_m' B$, for some $\chi_m$ and a related $\chi_m'$, and computed the magnetic surface currents from the magnetization, and then used Biot-Savart to find the magnetic field, it would be an extremely complex calculation, in the sense that you would need to guess a magnetic field solution $B$ everywhere which would cause magnetization $M$ that would likely be somewhat non-uniform, and the $B$ that was computed from the magnetic currents that arose from the magnetization $M$ would need to be equal to the "guess" for $B$ that was proposed. If the original guess was a rather good one, the actual magnetization $M$ and the actual $B$ could be ultimately determined in an iterative and self-consistent manner. This approach is, at best, still a very difficult one. $\\$ The method that is normally used for this problem,[Edit: "magnetic circuit theory"], involves using a modified form of ampere's law $\oint H \cdot dl=NI$, and assuming $H$ is constant throughout each material, and is $H_1$ in the air gap, and $H_2$ in the iron. This is clearly using an approximation to arrive at the answer, but it gets an answer that has been verified repeatedly with experimentation that has shown it to be reasonably accurate, so it is considered the accepted way of solving this problem. $\\$ The alternative method of Biot-Savart and magnetic surface currents would likely get a similar answer with a very lengthy and cumbersome process of calculation, but in general, this problem of the magnetic transformer with an air gap simply is not done in this manner. $\\$ [Edit: There is also a magnetic "pole" method of doing magnetostatic calculations, that is equivalent to the surface current method, but sometimes gets to the answer a little quicker. In any case, I don't see any easy way of getting any quick results with the transformer with an air gap problem by using these alternative techniques].

 

[Charles Link]

@mertcan See the [Edit: additions] on post 11 above in two places. $\\$ And see also: http://www.nptel.ac.in/courses/Webcourse-contents/IIT%20Kharagpur/Basic%20Electrical%20Technology/pdf/L-21%28TB%29%28ET%29%20%28%28EE%29NPTEL%29.pdf for magnetic circuit theory where they even mention Biot-Savart techniques in the opening paragraph (21.1).

 

[mertcan]

The magnetic surface currents are present even in the static case, and occur also in a permanent magnet. The magnetic field for any magnet can be computed from Biot-Savart (or Ampere's law) if the magnetization $\vec{M}$ is known, so that the surface currents can be computed. (In complete detail, the magnetic current density $\vec{J}_m=\frac{\nabla \times \vec{M}}{\mu_o}$. The result is that there are surface currents at boundaries given by surface current per unit length $\vec{K}_m=\frac{\vec{M} \times \hat{n}}{\mu_o}$, but there can also be magnetic current densities in the bulk material in regions of non-uniform $\vec{M}$). $\\$ For a somewhat detailed example of the magnetic surface currents, see https://www.physicsforums.com/threads/magnetic-field-of-a-ferromagnetic-cylinder.863066/

thanks for return @Charles Link but according to faraday law change of magnetic field results in current or voltage but you say even we have no time varied current in transformer which also means no time varied magnetic field we again have surface currents. What is origin of those type of currents?

 

[Charles Link]

thanks for return @Charles Link but according to faraday law change of magnetic field results in current or voltage but you say even we have no time varied current in transformer which also means no time varied magnetic field we again have surface currents. What is origin of those type of currents?

The Faraday effect of time variation is another problem. The Faraday EMF can create additional circulation of currents: Compute the direction=these are circular currents inside the material=these are in addition to magnetic surface currents but circulate in the opposite direction. They are often referred to as "eddy" currents, but therei s a simple solution for them: Transformers are often made in laminated layers to block these eddy currents. In these eddy currents, there is actual electrical charge transport, unlike the magnetic surface currents that are like the net result of a current circulating on the edges of eacgh square of a checkerboard, e.g. in the counterclockwise direction. The currents in adjacent squares will cancel, with the net result being a current along the outer edge of the board. With the magnetic surface currents, there is no charge transport=they are the result of "bound" quantum states in the same (e.g. counterclockwise) direction. Thereby, the laminated layers of a transformer do not block them, and the magnetic field from the surface currents occurs just as it should, and with very little eddy current in the material. The magnetic field $\vec{B}$ in a transformer is basically the result of the magnetic surface currents, computed from Biot-Savart and/or Ampere's law. You also need to add the contribution from the primary windings, (using Biot-Savart and/or Ampere's law), but if $\mu_r=500$ or more, the magnetic field is mostly from the magnetic surface currents.

 

[Charles Link]

@mertcan There is one more important practical detail that arises in these transformer equations, that probably isn't completely obvious from looking at the equations that have been considered so far in this thread. The current balance equation equation $N_p I_p=N_s I_s$ seems to be somewhat universal. $\\$ From Faraday's law $\mathcal{E}=-\frac{d \Phi}{dt}$, the result is the EMF in the secondary will be related to the EMF in the primary by the ratio of the number of turns: $\frac{\mathcal{E}_s}{\mathcal{E}_p}=\frac{N_s}{N_p}$. This is a voltage-based equation. [Editing: I made an error or two, so I revised this part]. $\\$ The law of current balance, $N_p I_p=N_s I_s$, a current-based equation, is also important in treating transformer circuits. Anyway, I think you might find the following thread of interest, where the current balance law is discussed, and particularly posts 25-29 : https://www.physicsforums.com/threa...ce-in-transformers.941936/page-2#post-5960705 $\\$ A little algebra with these two equations gives $\mathcal{E}_s I_s=\mathcal{E}_p I_p$, as expected from power considerations.

 

[Charles Link]

And a follow-on: A slight puzzle arises on this one: I'd like to ask @jim hardy for his input to see if I have resolved it correctly: $\\$ Without any load=no secondary current, the transformer will develop a voltage that is a result of $\mathcal{E}=-\frac{d \Phi}{dt}$, and the magnetic flux $\Phi$ is in phase with the primary current. This means the voltage on the primary coil at zero load on the secondary will be 90 degrees out of phase with the (magnetizing) current from the primary. Now we are going to assume here that we are driving the primary coil with a voltage source that can deliver whatever current it needs to to maintain the voltage. $\\$ Let's assume we now attach a small resistor to the secondary,(a significant load). There will be current in the secondary that is in phase with the voltage that is generated in the primary and secondary from Faraday's law. This secondary current must be necessarily 90 degrees out of phase from the zero load (magnetizing) current of the primary. In addition, the equations that we have suggest there must necessarily be an increased current in the primary. This new current must satisfy $N_p I_p=N_s I_s$. It would appear that this primary current must be in phase with the secondary current, and thereby will be in phase with the primary voltage. That would be expected from power considerations=this primary current needs to be in phase with the primary voltage, and not 90 degrees out of phase. $\\$ A general comment here: The equations of magnetic coupling appear a little odd. Basically, because we are driving the circuit with a constant ac voltage, we are ensuring that $\frac{d \Phi}{dt}$ remains unchanged by any loading that occurs. It also appears that in putting a load on the secondary, the impedance of the transformer as seen by the voltage driving circuit has gone from inductive to resistive in its characteristics. In addition, putting a smaller resistor on the load will result in a smaller resistance of the transformer as seen by the voltage driving circuit. @jim hardy Might this be correct?

 

[jim hardy]

A general comment here: The equations of magnetic coupling appear a little odd. Basically, because we are driving the circuit with a constant ac voltage, we are ensuring that dΦdtdΦdt \frac{d \Phi}{dt} remains unchanged by any loading that occurs. It also appears that in putting a load on the secondary, the impedance of the transformer as seen by the voltage driving circuit has gone from inductive to resistive in its characteristics. In addition, putting a smaller resistor on the load will result in a smaller resistance of the transformer as seen by the voltage driving circuit. @jim hardy Might this be correct?

Those statements are correct for the way we use most transformers, exciting them with sinewave voltage to move power.
I'm working on a basic explanation at nuts&bolts level, almost finished but my alleged brain is fried at the moment.

Will try to post it in the morning.

Transformers are beautifully self balancing and that's how the early experimenters described them in 1800's.
When they closed the magnetic circuit it was an AHA! moment.old jim

 

[jim hardy]

Charles - i got past my confusion on dots and flux direction...

I am one of the less capable mathematicians here on PF
so kindly excuse the less-than-academic nature of this post.

I will describe the thought steps i use to get a mental picture of what's going on in a transformer. From that i can figure out a formula to approach most any problem i encounter.

Without any load=no secondary current, the transformer will develop a voltage that is a result of E=−fracdΦdtE=−fracdΦdt \mathcal{E}=-frac{d \Phi}{dt} , and the magnetic flux ϕϕ \phi is in phase with the primary current. This means the voltage on the primary coil at zero load on the secondary will be 90 degrees out of phase with the current from the primary. Now we are going to assume here that we are driving the primary coil with a voltage source that can deliver whatever current it needs to to maintain the voltage. \\

To what degree of precision do we wish to describe the transformer ?

Your words above describe an ideal or near ideal transformer quite well. That would be one with zero resistance in its primary winding assuring 90 degrees between primary voltage and current.

A truly ideal transformer would have infinite inductance hence zero magnetizing current but we won't push our analysis to that extreme, just it's a point to be aware of.

Energy lost in the core looks like resistance in parallel , but for right now let's assume it's little enough energy we can ignore it. In a good transformer that's not far from the truth..

SO yes, with sinewave excitation constant voltage means constant flux. I use volts per turn as a measure of flux.

Let's assume we now attach a small resistor to the secondary,(a significant load). There will be current in the secondary that is in phase with the voltage that is generated in the primary and secondary from Faraday's law. This secondary current must be necessarily 90 degrees out of phase from the zero load current of the primary. In addition, the equations that we have suggest there must necessarily be an increased current in the primary. This new current must satisfy NpIp=NsIsNpIp=NsIs N_p I_p=N_s I_s . It would appear that this primary current must be in phase with the secondary current, and thereby will be in phase with the primary voltage. That would be expected from power considerations=this primary current needs to be in phase with the primary voltage, and not 90 degrees out of phase. \\

I think in terms of MMF's and let flux be MMF/Reluctance(of magnetic path). Remember units of MMF is amp-turns .

And being really a plodder i think in small simple steps.

Magnetizing current will be whatever amp-turns are required to push enough flux around the core to make a counter-emf equal to applied voltage.

A low reluctance core , ie good steel with no air gap will require very little MMF hence little magnetizing current.

A core with an air gap like you drew in first post will need a lot more amp turns to push the necessary flux through that gap. Magnetizing current will be higher.

So let's stick with a gapless core.Now let secondary current flow. That current produces MMF that opposes primary MMF.

So primary current must change to restore flux and counter-emf to match the voltage applied to primary windings. But how does it change ?

Primary and secondary voltage must be in phase with one another because they're both the derivative of the same flux.

Secondary current has to be in phase with secondary voltage because the load is defined, for this thought experiment, as resistive.

So secondary current makes MMF that's out of phase with flux . Secondary current and MMF are both in phase with derivative of flux..

Hmm. Plodding along here,

Flux has to remain constant , defined by the applied voltage which we are holding constant for this thought experiment.

And since flux is ∑MMF's/ Reluctance and reluctance is constant

that means primary current must change to make a MMF that's equal and opposite to secondary MMF. Else sum of MMF's won't equal magnetizing MMF.

Well, MMF's are directly proportional to current, no derivative,

so primary current will pick up a component that's in phase with derivative of flux to balance the one from secondary current.Now Faraday's Law acquires a minus sign when we incorporate Lenz's Law and you'll often see e = -NdΦ/dt and that can get confusing.

Add to that, transformers are usually drawn with flux going up one leg and down the other.

That's why we use the "Dot" convention. Dotted terminals will all move positive together, ie they're in phase.

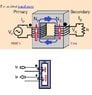
But I resort to pictures. Snip from Hyperphysics, i don't think they mind so long as i credit them and don't cause lots of traffic there...

In top image

i added dots and arrows for flux and mmf.

Dot convention = dotted terminals will be positive at same instant. That's how you get phasing right.

Observe current ENTERS primary's dotted terminal but LEAVES secondary's dotted terminal. By right hand rule that gives upward MMF's in both windings .

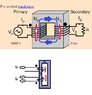
Secondary MMF is Counterclockwise opposing Clockwise primary MMF . Lenz's law at work.In Bottom image

I just moved secondary over to same side of core as primary . That makes one MMF point up and one down. Look carefully, i was rigorous to preserve winding directions relative to flux.
That helps some folks visualize right hand rule . It helps me remember that, in most training materials, the windings are drawn encircling the flux in opposite directions, Viewed from the top, primary is wound CCW and secondary is CW. It might be clearer drawn this way with primary and secondary both wound same direction..…

That removes the confusion factor of winding direction. I need things simple.

..................................

All that having been said ,
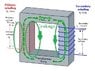
now i want to point you toward Wikipedia's electrical model of a transformer . It's a pretty good thought tool. It's at https://en.wikipedia.org/wiki/Transformer

Rp and Xp repesent primary winding's leakage inductance and resistance.
Rc represents energy loss in the core due to eddycurrents, hysteresis , magnetorestriction ...
The transformer in the middle is ideal - zero magnetizing current , infinite inductance.
Xm represents the actual finite mutual inductance of the transformer.
Io is sum magnetizing current that makes flux and current that goes into core losses, ie heating the iron.
Rs and Xs are resistance and leakage inductance of the secondary winding.

Leakage inductance is present because of flux that doesn't couple both windings..
From the Wiki transformer page:

i just drew in a few loops of leakage flux..

I hope the above is of help to you.
As i say, when i get a mental picture that leads me to the right equation i can trust both.

old jim

 

[Charles Link]

Thanks @jim hardy That was very helpful. It helped confirm a couple of my ideas in my post above. Right now, I like to work with a somewhat ideal transformer that may even have an air gap to give finite magnetizing currents, but computations with details such as core resistance and heating from eddy currents and hysteresis is more specialized than I presently need. $\\$ One additional item I mentioned above is laminations that are sometimes used to minimize eddy currents. Are these laminations a necessity, and how effective are they in minimizing eddy currents? And thanks again for your excellent inputs @jim hardy :) :)

 

[jim hardy]

computations with details such as core resistance and heating from eddy currents and hysteresis is more specialized than I presently need. \\

They are indeed complex. That was one of Steinmetz's contributions to the field, with his equation it became possible to design cores instead of trial and error them.
Search terms 'steinmetz equation magnetic losses' http://web.eecs.utk.edu/~dcostine/ECE482/Spring2015/materials/magnetics/CoreLossTechniques.pdf

Are these laminations a necessity, and how effective are they in minimizing eddy currents?

They are indeed necessary.
Magnetization proceeds from the periphery toward the center of a piece of iron, because eddy currents oppose the change in flux per Lenz.
A solid unlaminated core, above some frequency, might as well not have any iron in the center.
Laminations impede eddy currents allowing your core to use its whole cross section to conduct flux. Analogous to skin effect in wires carrying current.

I once measured an inductor with a core made of unlaminated 400 series stainless steel bar stock. Above 3 hz it was really not a good inductor.

here is its response to triangle wave current at 3hz, 10 hz, and 60 hz.
Triangle wave has constant di/dt so should produce square wave voltage. Sinewave only gives phase shift, triangle wave makes the effect a lot more obvious to the eye
Observe voltage is di/dt only at low frequency

That system ran at 60 hz. It had terrible drift with temperature because resistivity of steel is a strong function of temperature, and eddy currents follow it.

old jim

 

[Charles Link]

They are indeed necessary.
Magnetization proceeds from the periphery toward the center of a piece of iron, because eddy currents oppose the change in flux per Lenz.
A solid unlaminated core, above some frequency, might as well not have any iron in the center.

Thank you @jim hardy Very helpful inputs. $\\$ One thing perhaps worth mentioning is that I think the physics books and physics curriculum of my generation, college days 1975-1980, really sidestepped the whole subject of magnetization/magnetostatics in treating transformers. They taught us even some of the finer details of Maxwell's equations, but they omitted the application of a variation of Ampere's law: $\oint H \cdot dl=NI$ which leads to the magnetic circuit equations. $\\$ It is so good to have the Physics Forums to fill in these "gaps", including the problem of the transformer with an air "gap", (no pun intended). :)

 

[jim hardy]

I was in school perhaps ten years before you. We only studied Maxwell's equations in physics courses. Electric machinery course treated magnetics as a magnetic circuit, and that's how i still approach magnetics problems.

For a machine where virtually all the flux stays inside the iron it works well enough for slide rule accuracy. I've walked around huge machines with a search coil connected to a battery powered oscilloscope and indeed the field around them is nil. Where i found large fields was in the vicinity of air core inductors and high current busbars.

 

[Charles Link]

I was in school perhaps ten years before you. We only studied Maxwell's equations in physics courses. Electric machinery course treated magnetics as a magnetic circuit, and that's how i still approach magnetics problems.

Perhaps the instruction has changed since then. In any case, the magnetic circuit equations, IMO, should not be the exclusive domain of the EE (electrical engineer). It has such a widespread application in what are countless transformers everywhere. For a physics person to be able to call himself an "expert" on Maxwell equations, he should also be able to perform at least simple computations with the magnetic circuit equation, that actually originates from a form of Maxwell's Ampere's Law equation.

 

[mertcan]

The Faraday effect of time variation is another problem. The Faraday EMF can create additional circulation of currents: Compute the direction=these are circular currents inside the material=these are in addition to magnetic surface currents but circulate in the opposite direction. They are often referred to as "eddy" currents, but therei s a simple solution for them: Transformers are often made in laminated layers to block these eddy currents. In these eddy currents, there is actual electrical charge transport, unlike the magnetic surface currents that are like the net result of a current circulating on the edges of eacgh square of a checkerboard, e.g. in the counterclockwise direction. The currents in adjacent squares will cancel, with the net result being a current along the outer edge of the board. With the magnetic surface currents, there is no charge transport=they are the result of "bound" quantum states in the same (e.g. counterclockwise) direction. Thereby, the laminated layers of a transformer do not block them, and the magnetic field from the surface currents occurs just as it should, and with very little eddy current in the material. The magnetic field $\vec{B}$ in a transformer is basically the result of the magnetic surface currents, computed from Biot-Savart and/or Ampere's law. You also need to add the contribution from the primary windings, (using Biot-Savart and/or Ampere's law), but if $\mu_r=500$ or more, the magnetic field is mostly from the magnetic surface currents.

@Charles Link here you say there is no charge transport in magnetic surface currents but also you say in previous posts in order to apply biot savart you should also take magnetic surface currents. In biot savart I deem that real currents(which there is a charge transports) are included but if biot savart includes charge transport current and magnetic surface currents are no real charge transport why you say that in biot savart you should also include magnetic surface currents??

 

[Charles Link]

@Charles Link here you say there is no charge transport in magnetic surface currents but also you say in previous posts in order to apply biot savart you should also take magnetic surface currents. In biot savart I deem that real currents(which there is a charge transports) are included but if biot savart includes charge transport current and magnetic surface currents are no real charge transport why you say that in biot savart you should also include magnetic surface currents??

Suggestion is to see this "link" https://www.physicsforums.com/threads/magnetic-field-of-a-ferromagnetic-cylinder.863066/ This is an example of how magnetic surface currents are used in calculations. Griffiths E&M textbook derives the result that the magnetic surface current per unit length $K_m=\vec{M} \times \hat {n} /\mu_o$. Applying Biot-Savart to these magnetic surface currents does get the correct result for the magnetic field $B$ from them. $\\$ (This "link" was also given in post 4 of this same thread).

 

[mertcan]

Suggestion is to see this "link" https://www.physicsforums.com/threads/magnetic-field-of-a-ferromagnetic-cylinder.863066/ This is an example of how magnetic surface currents are used in calculations. Griffiths E&M textbook derives the result that the magnetic surface current per unit length $K_m=\vec{M} \times \hat {n} /\mu_o$. Applying Biot-Savart to these magnetic surface currents does get the correct result for the magnetic field $B$ from them. $\\$ (This "link" was also given in post 4 of this same thread).

In Griffiths book static case mostly is taken into account. If we have time varied current then we also include eddy currents as well as bound or surface currents?? Am I right?

 

[Charles Link]

In Griffiths book static case mostly is taken into account. If we have time varied current then we also include eddy currents as well as bound or surface currents?? Am I right?

The eddy currents I believe are a minor correction, and they are kept in check by laminations. See in particular posts 19 and 20 of this thread. $\\$ And yes, your analysis that the eddy currents could become very problematic is clearly the case, as stated by @jim hardy in post 20. $\\$ Additional comment: For the iterative method presented in post 11 using Biot-Savart, I would propose using the solution obtained by the "reluctance"/ "magnet circuit theory"/"modified Ampere's law" method as a "first guess" for $\vec{B}$ ,(as a function of position), and see if the $\vec{M}$ and the $\vec{ B}$ that get computed iteratively just may converge to a solution that is reasonably approximated by the "reluctance"/"magnetic circuit theory"/"modified Ampere's law" method. If the "first guess" is a good one, you could get rapid convergence and two or three decimal place accuracy within one or two iterations. (If the "first guess" is a poor one, it may not even start to converge after several iterative cycles). $\\$ And a couple of qualifying items are in order here =the above assumes the magnetic material responds linearly (in its magnetization $\vec{M}$ ) to the applied field at a given location. This may or may not be completely the case, and especially since magnetic materials get compounded by the exchange effect, so that what the nearest neighbors are doing can also affect the response at a given location. Thereby, Biot-Savart based solutions that also assume linear response in the materials may not be applicable in every single case.

 

[Charles Link]

@mertcan One thing worth mentioning here is that Biot-Savart's law, $\vec{B}(\vec{r})=\int (\frac{\mu_o}{4 \pi}) \frac{\vec{J}(r')_{total} \times (\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3} \, d^3 \vec{r}'$, is the solution for $\vec{B}$ of the differential equation which is Ampere's law: $\nabla \times \vec{B}=\mu_o \vec{J}_{total}$, where $\vec{J}_{total}=\vec{J}_{conductors}+\vec{J}_m +\vec{J}_p$. $\\$ (This steady state form of Ampere's law omits the term $\mu_o \epsilon_o \frac{d \vec{E}}{dt}$). $\\$ Here $\vec{J}_m=\frac{\nabla \times \vec{M}}{\mu_o }$, (gradients in the magnetization vector $\vec{M}$ result in magnetization currents), and $\vec{J}_p=\frac{d \vec{P}}{dt}$. $\\$ From the equation $\vec{J}_m=\frac{\nabla \times \vec{M}}{\mu_o }$, and from Stokes' theorem, the result follows that the magnetic surface current per unit length at a surface boundary is $\vec{K}_m=\frac{\vec{M} \times \hat{n}}{\mu_o}$. Thereby the Biot-Savart equation as shown also includes the magnetic surface currents. $\\$ The magnetic circuit theory equation $\oint \vec{H} \cdot dl =NI$ is a modified form of Ampere's law in integral form, where the result $\vec{B}=\mu_o \vec{H} +\vec{M}$ is also used. (The equation $\vec{B}=\mu_o \vec{H}+\vec{M}$ can be derived using Biot-Savart. It is a somewhat lengthy derivation. The field $\vec{H}$ needs to be defined so that it includes contributions from magnetic poles. The magnetic pole contribution to $\vec{H}$ always obeys $\oint \vec{H} \cdot dl=0$). $\\$ Taking $\nabla \times \vec{B}= \nabla \times ( \mu_o \vec{H}+ \vec{M})=\mu_o (\vec{J}_{conductors}+\vec{J}_m)$, (and ignoring the $\vec{J}_p$ term), the term $\nabla \times \vec{M}$ cancels the $\mu_o \vec{J}_m$ term, with the result that $\nabla \times \vec{H}=\vec{J}_{conductors}$. This equation can be integrated over a surface, in this case the surface being one whose outer perimeter is a ring that takes the path through the center of the transformer, and Stokes' theorem applied, with the result that $\oint \vec{H} \cdot dl=NI$ where the factor $N$ is for the number of turns of transformer winding. $\\$ Thereby, these two forms=Biot-Savart and the magnetic circuit theory equation, are equivalent. The magnetic circuit theory solution makes an approximation that $\vec{B}$ is completely continuous, (it follows from $\nabla \cdot \vec{B}=0$, and if zero flux leakage occurs, $\vec{B}$ takes on a constant and continuous form ), and also assumes a linear material so that $\vec{M}=\mu_o \chi_m \vec{H}$ with the result that $\vec{B}=\mu_r \mu_o \vec{H}$, Another approximation is made in this solution, since $\vec{B}$ is assumed continuous, that $\vec{H}$ stays constant in each material. $\\$ This magnetic circuit theory equation, since it is a result of Maxwell's Ampere's law in differential form, is actually equivalent to a Biot-Savart solution. The additional approximations that it makes is a shortcut to arriving at the final solution. A completely detailed Biot-Savart solution with surface currents, that doesn't assume $\vec{H}$ to be continuous in each material, will be mathematically much more cumbersome, but is likely to result in a solution that comes close to the magnetic circuit theory solution with its approximation of $\vec{H}$ being constant throughout each given material. $\\$ (The Biot-Savart solution would work iteratively with $\vec{B}$ and $\vec{M}$, as described in post 11, and once a solution was found, $\vec{H} =\frac{\vec{B}}{\mu_o \mu_r}$ could be computed for each region and compared with the magnetic circuit theory result. Since $\vec{M}=\mu_o \chi_m \vec{H}$, and $\vec{B}=\mu_o \mu_r \vec{H}$, it is possible to write an equation of the form $\vec{M}=\chi'_m \vec{B}$ in working to a solution. That way, there is no need to keep track of a 3rd parameter, $\vec{H}$, in working the Biot-Savart solution).

 

[Charles Link]

One additional item comes up in the solution of this problem: You may ask, if we can solve $\nabla \times\vec{B}$ with a closed-form Biot-Savart integral solution, why don't we simply use it to solve the equation $\nabla \times \vec{H}=\vec{J}_{conductors}$ the very same way? $\\$ And the reason is that with this last equation, there are homogeneous solutions that have $\nabla \times \vec{H}=0$ that need to be included. This missing contribution to $\vec{H}$ can be shown to come from the magnetic pole terms, ( where magnetic pole density $\rho_m =-\nabla \cdot \vec{M}$ are sources for $\vec{H}$ in the magnetic pole model). This magnetic pole contribution to $\vec{H}$ has $\nabla \times \vec{H}=0$ and the Biot-Savart type solution for $\vec{H}$ fails to generate this part of $\vec{H}$. $\\$ [Note: The magnetic "poles" are essentially a consequence of magnetic currents. Gradients in the magnetization vector $\vec{M}$ generate magnetic currents and magnetic poles. The magnetic poles are something of a mathematical construction, and are not considered to be sources of $\vec{B}$. They are used to compute $\vec{H}$ in the "magnetic pole model", which is an alternative method of computing $\vec{H}$ and $\vec{B}$, that gets the same answer for $\vec{B}$ as the "magnetic current" method. In the magnetic pole model method of doing the calculation, magnetic currents are ignored. In a magnetic current calculation using Biot-Savart's law to compute $\vec{B}$, the magnetic poles are ignored]. $\\$ Magnetic poles will have a vector $\vec{H}$ associated with them that would have a corresponding $\vec{B}$. By missing this part of the $\vec{H}$ with a Biot-Savart type solution for $\vec{H}$, it will result in missing part of the $\vec{B}$. $\\$ In the case of the transformer, we see that we would simply generate the field $\vec{H}$ from the current in the transformer windings without any modification for the presence of the transformer core. Clearly, the Biot-Savart solution for $\vec{H}$, using $\vec{H}(\vec{r})=\int (\frac{1}{4 \pi}) \frac{\vec{J}(r')_{conductors} \times (\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3} \, d^3 \vec{r}'$, is an incomplete solution for $\vec{H}$. $\\$ [Edit: Once the assumption is made that the core causes the current in the windings to be spread out uniformly around the core as a current per unit length of $K=\frac{NI}{L+d}$, a Biot-Savart/Ampere's law based solution for the magnetization $M$ and the magnetic field $B$ that uses magnetic surface currents is really quite straightforward]. $\\$ Meanwhile the Biot-Savart solution for $\vec{B}$, as given in post 28, is complete and does not require any additional homogeneous solutions. The biggest difficulty here is getting an accurate solution of the magnetization function $\vec{ M}$, and computing the resulting $\vec{J}_m=\frac{\nabla \times \vec{M}}{\mu_o }$ along with the resulting magnetic field $\vec{B}$. [Edit: With the method used as given in the "Edit" of the previous paragraph, the Biot-Savart/Amper's law solution for this transformer is really quite straightforward. The magnetic surface currents, that are generated over a length $L$, are also assumed to be spread out uniformly across the length $L+d$ in computing the magnetic field $B$ from them]. $\\$ The magnetic circuit theory solution, which actually begins with the integral and Stokes' theorem evaluation of $\nabla \times \vec{H}=\vec{J}_{conductors}$ , is [Edit:] really identical to a Biot-Savart/Ampere's law solution that assumes a uniform spreading of the current in the windings and the magnetic surface currents around the entire core].

 

[Charles Link]

And an additional comment or two on the magnetic circuit theory solution, which is also discussed in the Feynman lecture "link" of post 2 which I will repeat here: http://www.feynmanlectures.caltech.edu/II_36.html The equation of interest in the "link" is equation (36.26). $\\$ The solution assumes constant $H_1$ in the air gap and $H_2$ in the iron core, which are then determined. $\\$ Using a magnetic pole model of solution, if the magnetization $\vec{M}$ is constant, this will create poles of magnetic surface charge density $\sigma_m=+M$ and $\sigma_m=-M$ on either side of the gap. For a small gap, this looks like two infinite planes of magnetic surface charge, so that the $H$ that is computed will be (approximately) constant across the air gap. $\\$ Similarly, if $M$ is constant in the material, the $H$ will be constant in the material. The two opposite poles on either side of the air gap are adjacent to each other, so the $H$ that they cause in the iron core is essentially zero. In any case, there will be a very small residual $H_2$ in the iron, which is assumed to be constant throughout the iron core. $\\$ The magnetic circuit theory (Feynman's solution) makes use of these observations and assigns $H_1$ to the air gap and $H_2$ to the iron core and computes the integral, with the additional assumption that $B$ is constant/continuous around the loop of the path of integration in these equations. The fact that $B$ is nearly continuous is justification for $M$ and $H_2$ being nearly constant. The magnetic circuit theory gets the answer for $H_1$ in the air gap without even doing the magnetostatic problem of two infinite sheets of magnetic surface charge density $\sigma_m=\pm M$, and gets essentially the same answer $H_1= \frac{M}{\mu_o}+H_2$ that the magnetostatic computation would give. (The magnetostatic calculation for the two infinite sheets of magnetic charge density gives $H_s=\frac{M}{\mu_o}$ . Superimposed on that is $H_2$ (typically small for large $\mu$) to give $H_1=H_s+H_2$). $\\$ A completely Biot-Savart approach, without a couple of useful observations to aid in a "first guess" solution would be very difficult.$\\$ [Edit: Using the methodology of the [Edit] comments at the bottom of post 29, we effectively have a Biot-Savart/Ampere's law based solution that is quite straightforward]. Using this "first guess" it would be possible to obtain an iterative solution of $B$ and $M$ using Biot-Savart for $B$ as discussed in post 28. The final result will likely not differ a whole lot from the "first guess". And a toroidal shaped core would require fewer corrections than a rectangular shaped core. $\\$ [Edit: It is perhaps worth mentioning that for large $\mu_r$, the magnetic surface currents per unit length are many, many times larger than $K_{average}=\frac{NI}{L+d}$ , so that it takes only a very minor adjustment in the function $\vec{M }$ to generate magnetic poles from gradients in $\vec{M}$ to create a function $\vec{H}$, that spreads itself uniformly around the core. The magnetization $\vec{M}$ can readily supply the necessary homogenous solution for $\vec{H}$ from the magnetic poles that completes the solution to $\vec{H}$. Thereby, the Biot-Savart solution for $\vec{H}_{conductors}$ is, as was previously mentioned (post 29), very incomplete, but the complete $\vec{H}$ that occurs, is readily found, and quite accurately, with the assumption that $\vec{B}$ is continuous around the path through the core].

 

[vanhees71]

The magnetic surface currents are present even in the static case, and occur also in a permanent magnet. The magnetic field for any magnet can be computed from Biot-Savart (or Ampere's law) if the magnetization $\vec{M}$ is known, so that the surface currents can be computed. (In complete detail, the magnetic current density $\vec{J}_m=\frac{\nabla \times \vec{M}}{\mu_o}$. The result is that there are surface currents at boundaries given by surface current per unit length $\vec{K}_m=\frac{\vec{M} \times \hat{n}}{\mu_o}$, but there can also be magnetic current densities in the bulk material in regions of non-uniform $\vec{M}$). $\\$ For a somewhat detailed example of the magnetic surface currents, see https://www.physicsforums.com/threads/magnetic-field-of-a-ferromagnetic-cylinder.863066/

[Later note:] There seems to be varying conventions in the physics and electrical-engineering literature: I've just checked Simonyi's comprehensive textbook on "theoretical electric engineering" (the title of my German edition is "Theoretische Elektrotechnik", I don't know, whether this amazing book is available in English; it's simply great!) for another question preparing my lecture notes. There I stumbled over the surprising fact that he defines the magnetization as part of $\vec{B}$. As I write below, for me as a physicist used to interpreting everything from the point of view of the fundamental principles, the magnetization should clearly belong to $\vec{H}$, because it's an external source for the magnetic field $\vec{B}$. There seems to be more historical balast in E&M than I ever dreamt of ;-))). Of course, at the end both conventions lead to the correct result, the only difference is that $\vec{M}_{\text{engineers}}=\mu_0 \vec{M}_{\text{physicists}}$, i.e., the constitutive equation reads
$\vec{B}=\mu_0 \vec{H} + \vec{M}_{\text{engineers}} \equiv \mu_0 (\vec{H}+\vec{M}_{\text{physicists}}$ ;-)).

Just a hint. I'm teaching E&M right now to high school-teacher students, and there I've of course to stick to the SI units. So I'm a bit thinking how to explain to the students the somewhat idosyncratic terminology of permittivities and permeabilities occurring in opposite ways (and even occurring for the vacuum just because of the SI units), because in the early days of electromagnetism the physicists somehow mixed up $\vec{H}$ and $\vec{B}$. It's very important not to confuse where the $\mu_0$ (or $\mu=\mu_0 \mu_{\text{r}}$ in para- and diamagnetic substances) occur.

For hard ferromagnetics you only give the magnetization (magnetic-dipole density per unit volume) and assume full saturation. The magnetization belongs to the "excitation quantities", i.e., to the "magnetic excitation" $\vec{H}$ rather than the "magnetic field" $\vec{B}$, where I use the modern naming scheme following from the physical meaning and relativity, where $\vec{E}/c$ and $\vec{B}$ together form an antisymmetric four-tensor as well as $\vec{D}$ and $\vec{H}$. Physically $\vec{E}$ and $\vec{B}$ are the fields occurring in the Lorentz force law, while $\vec{D}$ and $\vec{H}$ are auxilliary quantities to separate the external (or "free") sources from the sources due to the presence of matter from bound charges (i.e. the electric and magnetic dipole moments induced by the perturbation through the fields produced by the free charges and current densities).

Thus for hard ferromagnetics the basic static equations read
$$\vec{\nabla} \times \vec{H}=\vec{j}_f, \quad \vec{\nabla} \cdot \vec{D}=\rho_f, \quad \vec{\nabla} \times \vec{E}=0, \quad \vec{\nabla} \cdot \vec{B}=0$$
and the constitutive equations
$$\vec{D}=\epsilon_0 \epsilon_r \vec{E}, \quad \vec{B}=\mu_0 (\vec{H}+\vec{M}),$$
where $\vec{M}$ is the magnetization unchanged by external influence due to the presence of hard ferromagnets. The electric and magnetic fields decouple completely, and the electric part is just as in electrostatics. So we can concentrate on the magnetic fields.

In this most general case for static fields, i.e., with currents in addition to permanent magnetization present, the most general way to solve the equations is to introduce the vector potential for $\vec{B}$. For the case without currents, $\vec{H}$ is curl-free and you can simplify the task somewhat by introducing a magnetostatic potential for $\vec{H}$.

The first method, which applies everywhere in the most general static case, you get formally vacuum equations for $\vec{B}$ with an effective current composed by the free current and the curl of the magnetization. This becomes clear by taking the curl of the 2nd constitutive equation and using Ampere's Law for $\vec{H}$:
$$\vec{\nabla} \times \vec{B}=\mu_0 \vec{\nabla} \times (\vec{H}+\vec{M}) = \mu_0 (\vec{j}_e + \vec{j}_m), \quad \vec{j}_m=\vec{\nabla} \times \vec{M}.$$
Here $\vec{j}_e$ and $\vec{j}_m$ are usually considered to be given. If one assumes $\vec{M}$ to be constant within the magnet and (of course) jumps instantaneously to 0 at the boundary of the magnet, its curl leads to a singular $\delta$-function like $\vec{j}_m$ which is equivalent to a surface current along the boundary surface of the magnet. This is in some sense in accordance with Ampere's old molecular-current hypothesis, which of course today must be substituted by the proper quantum-mechanical treatment. For the phenomenology it's just a calculational trick to substitute the approximate analysis with homogeneous magnetization within the magnet by the equivalent surface current given also in this case by $\vec{\nabla} \times \vec{M}$, leading however to a $\delta$-distribution due to the jump at the boundary.

In any case the solution lies in the introduction of the vector potential. Due to gauge freedom we can also impose a gauge constraint, which in this static case is most conveniently chosen as the Coulomb gauge, i.e., we set
$$\vec{B}=\vec{\nabla} \times \vec{A}, \quad \vec{\nabla} \cdot \vec{A}=0,$$
and for Cartesian components we can thus write
$$\vec{\nabla} \times \vec{B}=\vec{\nabla} \times (\vec{\nabla} \times \vec{A})=-\Delta \vec{A}=\mu_0 \vec{j}, \quad \vec{j}=\vec{j}_f + \vec{\nabla} \times \vec{M}$$
with the Biot-Savart-like solution
$$\vec{A}(\vec{r}) = \mu_0 \int_{\mathbb{R}^3} \mathrm{d}^3 r' \frac{\vec{j}(\vec{r}')}{|\vec{r}-\vec{r}'|},$$
or for the field
$$\vec{B}(\vec{r}) =\nabla \times \vec{A}(\vec{r})=\mu_0 \int_{\mathbb{R}^3} \mathrm{d^3} r' \vec{j}(\vec{r}') \times \frac{\vec{r}-\vec{r}'}{|\vec{r}-\vec{r}'|^3}.$$
This is Biot-Savart's Law in its usual form but with the total current density including the effective magnetization current.

If somebody is interested in my German manuscript for these lectures (unfinished, but quickly growing ;-)), here they are:

https://th.physik.uni-frankfurt.de/~hees/publ/theo2-l3.pdf

 

[Charles Link]

For hard ferromagnetics you only give the magnetization (magnetic-dipole density per unit volume) and assume full saturation.

Normally, the only quantities of interest for permanent magnets are $\vec{M}$, and $\vec{B}$, but the relation $\vec{B}=\mu_o(\vec{H}+\vec{M})$ can still be used. The vector $\vec{H}$ is useful in the "magnetic pole model" of computing $\vec{B}$ both inside and outside of the permanent magnet.$\\$ For permanent magnets, there is no longer a linear relationship between $\vec{H}$ and $\vec{M}$. An equation can still be written as before $\vec{M}=\chi_m \vec{H}$, but for this case, $\chi_m$ is no longer a constant. The vectors $\vec{H}$ and $\vec{M}$ can at times even point in opposite directions, (making $\chi_m$ negative), depending on the location of the operating point of the magnetic material on the hysteresis curve. $\\$ The vector $\vec{H}$ is also useful in calculations with a permanent magnet if you want to determine the magnitude of $\vec{H}$ from the currents of a solenoid that surrounds that magnet that would be required to reverse the direction of magnetization. Even though in most cases the permanent magnet isn't placed inside a solenoid, it can still be a useful scenario to consider. The same equation $\vec{B}=\mu_o(\vec{H}+\vec{M})$, that is often used in calculations with linear magnetic materials, is still applicable for permanent magnets. $\\$ In the transformer core problem given in the OP by @mertcan , the very interesting feature is how the magnetic field $\vec{H}$ that is generated by the current in the windings is totally reshaped and amplified by the magnetic core, but the magnetic field $\vec{B}$ and the magnetization $\vec{M}$ are kept at a very stable and controlled amount by the presence of the air gap. The magnetic circuit theory solution, which is presented in Feynman's lectures, is equivalent to a Biot-Savart/Ampere's law solution, as discussed in posts 28, 29, and 30 above.

 

[jim hardy]

Even though in most cases the permanent magnet isn't placed inside a solenoid, it can still be a useful scenario to consider.

These folks have a small production facility just around the corner from me

https://azind.com/permanent-magnets/
I usually stop by their annual 'yard sale' because they sell really strong magnets .. It's fun to watch the ladies magnetize them . They use a solenoid about a foot tall and half as wide made of huge wire. It's amazing to see an inert blank turned into a giant 'fridge magnet' that tries to pull your carkeys out of your pocket when you walk by.

I found this tutorial on their site . It appears to be quite practical and surprisingly thorough - maybe it'll be of help to @vanhees71 with his presentations for lay people.
https://azind.com/wp-content/uploads/2014/11/Permanent-Magnet-Guidlines-MMPAPMG-88.pdf
I saved a copy to my PF folder for reference so i can read it off line.

I really should learn more about the science behind modern magnetic materials.

In the transformer core problem given in the OP by @mertcan , the very interesting feature is how the magnetic field →HH→ \vec{H} that is generated by the current in the windings is totally reshaped and amplified by the magnetic core, but the magnetic field →BB→ \vec{B} and the magnetization →MM→ \vec{M} are kept at a very stable and controlled amount by the presence of the air gap. The magnetic circuit theory solution, which is presented in Feynman's lectures, is equivalent to a Biot-Savart/Ampere's law solution, as discussed in posts 28, 29, and 30 above.

Well, thinking like a circuits fellow that's what iron does , it short circuits free space for magnetic flux. Air gap in a core becomes the controlling reluctance and iron's nonlinear and other peculiarities are minimal in comparison (unless you have enough mmf available to saturate it despite the gap.) .

I leave that vector calculus to you fellows. Please understand i do envy your fluency with it and that's not a dismissal .

old jim

 

[vanhees71]

Normally, the only quantities of interest for permanent magnets are $\vec{M}$, and $\vec{B}$, but the relation $\vec{B}=\mu_o(\vec{H}+\vec{M})$ can still be used. The vector $\vec{H}$ is useful in the "magnetic pole model" of computing $\vec{B}$ both inside and outside of the permanent magnet.$\\$ For permanent magnets, there is no longer a linear relationship between $\vec{H}$ and $\vec{M}$. An equation can still be written as before $\vec{M}=\chi_m \vec{H}$, but for this case, $\chi_m$ is no longer a constant. The vectors $\vec{H}$ and $\vec{M}$ can at times even point in opposite directions, (making $\chi_m$ negative), depending on the location of the operating point of the magnetic material on the hysteresis curve. $\\$ The vector $\vec{H}$ is also useful in calculations with a permanent magnet if you want to determine the magnitude of $\vec{H}$ from the currents of a solenoid that surrounds that magnet that would be required to reverse the direction of magnetization. Even though in most cases the permanent magnet isn't placed inside a solenoid, it can still be a useful scenario to consider. The same equation $\vec{B}=\mu_o(\vec{H}+\vec{M})$, that is often used in calculations with linear magnetic materials, is still applicable for permanent magnets. $\\$ In the transformer core problem given in the OP by @mertcan , the very interesting feature is how the magnetic field $\vec{H}$ that is generated by the current in the windings is totally reshaped and amplified by the magnetic core, but the magnetic field $\vec{B}$ and the magnetization $\vec{M}$ are kept at a very stable and controlled amount by the presence of the air gap. The magnetic circuit theory solution, which is presented in Feynman's lectures, is equivalent to a Biot-Savart/Ampere's law solution, as discussed in posts 28, 29, and 30 above.

For the case of no free currents, i.e., just the permanent magnet there are two possible equivalent ways to solve the problem. The equations then take the form
$$\vec{\nabla} times \vec{H}=0, \quad \vec{\nabla} \cdot \vec{B}=0, \quad \vec{B}=\mu_0(\vec{H}+\vec{M}).$$

1st strategy: Scalar potential for $\vec{H}$

Since $\vec{H}$ is vortex free, there's a scalar potential
$$\vec{H}=-\vec{\nabla} \phi_m.$$
Then we know that we also need its sources, and these are readily calulated using Gauss's Law for $\vec{B}$ and the constitutive equation
$$\vec{\nabla} \cdot \vec{H}=\vec{\nabla} \cdot (\vec{B}/\mu_0-\vec{M})=-\vec{\nabla} \cdot \vec{M}=\rho_m.$$
We have an effective magnetic charge, given by $\rho_m=-\vec{\nabla} \cdot \vec{M}$, and the solution is analogous to electrostatics
$$\phi_m(\vec{r})=\int_{\mathbb{R}^3} \mathrm{d}^3 r' \frac{\rho_m(\vec{r}')}{4 \pi |\vec{r}-\vec{r}'|}.$$
If there are jumps of $\vec{M}$ at the boundary, you get the usual "jump condition"
$$\Sigma_m=\vec{n} \cdot (\vec{H}_{>}-\vec{H}_{<}),$$
where $\Sigma_m$ is an effective magnetic surface charge. For the simplifying model of having $\vec{M}=\text{const}$ jumping at the surface of the magnet to 0, you only have this surface charge. This is also clear from the definition of the effective magnetic-charge density since taking the divergence of $\vec{M}$ leads to a $\delta$-distribution at the surface.

2nd stragey: Vector potential for $\vec{B}$

This way is working for all cases, i.e., even including free current densities. But let's stick to just the magnet without external currents. Then from Gauss's Law for $\vec{B}$ it's clear that there is a vector potential, fullfilling the Coulomb-gauge constraint
$$\vec{B}=\vec{\nabla} \times \vec{A}, \quad \vec{\nabla} \cdot \vec{A}=0,$$
and I need the vortices of $\vec{B}$ to get the sources for $\vec{A}$. Now we use the constitutive equations and the curl-freeness of $\vec{H}$ to get
$$\vec{\nabla} \times \vec{B}=-\Delta \vec{A}=\mu_0 \vec{\nabla} \times (\vec{H}+\vec{M})=\mu_0 \vec{\nabla} \times \vec{M}=\mu_0 \vec{j}_m.$$
The solution is Biot-Savart's Law for $\vec{B}$ with the effective magnetic current density $\vec{j}_m=\vec{\nabla} \times \vec{M}$ (see my previous posting). The boundary conditions are this time for $\vec{B}$
$$\vec{n} \cdot (\vec{B}_{>}-\vec{B}_{<})=0, \quad \vec{n} \times (\vec{B}_{>}-\vec{B}_<)=\mu_0 \vec{k}_m,$$
where $\vec{k}_m$ is an effective magnetic surface current (if present).

For the model with $\vec{M}=\text{const}$ jumping at the magnet's surface you get the surface current again by taking the curl of $\vec{M}$ which is then 0 everywhere, and you only have a surface current, given by a $\delta$-distribution valued $\vec{j}_m$.

Right now I'm preparing a section in my manuscript, where everything is analytically analyzed for the homogeneously magnetized sphere. Stay tuned :-).

The constitutive equation for a ferromagnet cannot be described by linear response theory anymore. You have a case of spontaneous symmetry breaking, and the constitutive relation depends on the history of the material. Heating it up without magnetic fields present, at a certain point the material will loose all magnetization. Then you can cool it down, and still there's no magnetization, but that's a metastable state since the magnetized state is energetically favored. Bringing the material in a magnetic field, the magnetization will grow from 0 to a certain saturation value and then stay there, even when switching the external magnetic field off. That's your permanent magnet. To demagnetize it you need a minimum external magnetic field, i.e., the constitutive law $\vec{M}=\vec{M}(\vec{H})$ is not going throuh 0 at $\vec{H}=0$. That's the famous hysteresis curve, shown in many textbooks. The most simple phenomenological theory is of course Ginzburg-Landau theory, i.e., the mean-field approximation for the many-body QFT describing the ferromagnetic medium.

 

[Charles Link]

For the first method above, where we have $\vec{B}=\mu_o(\vec{H}_m+\vec{M})$ without any free currents, this method can be expanded to include free currents. The $\vec{H}_{free}$ from the free currents is computed from Biot-Savart/Ampere's law and has for this contribution that $\vec{B}=\mu_o \vec{H}_{free}$. Thereby, if $\vec{H}$ is redefined to include the contribution from free currents, so that $\vec{H}=\vec{H}_m+\vec{H}_{free}$, this contribution to $\vec{H}$ can be added to both sides of the equation $\vec{B}=\mu_o(\vec{H}+\vec{M})$ and the equation $\vec{B}= \mu_o (\vec{H}+\vec{M})$ remains valid. In this case though, we no longer have $\nabla \times \vec{H}=0$, because $\nabla \times \vec{H}_{free}=\vec{J}_{free}$. $\\$ Basically the free current solution for $\vec{H}_{free}$ can be superimposed upon the solution for $\vec{H}_m$ that comes from a scalar potential $\vec{H}_m=-\nabla \phi_m$. (The scalar potential method requires $\nabla \times \vec{H}=0$ in order to work). $\\$ The reason why this solution with the $\vec{H}_{free}$ can be important, is that it is then possible to use the " magnetic pole model" method with the scalar potential $\phi_m$ to solve the problem that the OP has of a transformer with an air gap.

 

[vanhees71]

Yes, indeed. See my posting #31.

 

[jim hardy]

where →MM→\vec{M} is the magnetization unchanged by external influence due to the presence of hard ferromagnets.

So M then is remanent magnetism ?
Trying to nail down the terminology in my alleged mind.

THANKS - old jim

 

[Charles Link]

So M then is remanent magnetism ?
Trying to nail down the terminology in my alleged mind.

THANKS - old jim

Here $\vec{M}$ can be either a remanent=permanent magnetization that is virtually unchanged by any applied $\vec{H}$ field, or it can be the type that is found in a transformer where $\vec{M}=\chi_m \vec{H}$. $\\$ The equation $\vec{B}=\mu_o(\vec{H}+\vec{M})$ works for both types. The equation $\vec{B}=\mu_r \mu_o \vec{H}$ only works for the transformer type of magnetization. In that case $\mu_r=1+\chi_m$.

 

[vanhees71]

In general, ferromagnets can not be described by linear-response theory as can para- and diamagnets. The latter have
$$\vec{M}=\chi_m \vec{H},$$
where the magnetic susceptibility is a dimensionless number, with its modulus usually much smaller than one. A paramagnet had by definition $\chi_m>0$, a diamagnet $\chi_m<0$. A special case is a superconductor, where formally $\chi_m=-1$, i.e., it's a perfect diamagnet. The consitutive equation is in these cases linear, i.e.,
$$\vec{B}=\mu_0 (\vec{H}+\vec{M})=\mu_0 \mu_{r} \vec{H}, \quad \mu_r=1+\chi_m.$$
There's no magnetic field (traditionally called magnetic induction) $\vec{B}$ in the interior of a superconductor (which is an idealization of course).

For ferromagnets the relation between $\vec{H}$ and $\vec{M}$ is non-linear and not even unique. If you start with an unmagnetized piece of material, you get a curve starting from $0$ at $\vec{H}=0$. Beginning with large enough $|\vec{H}|$ the magnetization saturates, and you have $\vec{M}(\vec{H})=\text{const}$. When you now switch off $\vec{H}$, however, the magnetization doesn't go away completely again. For "hard ferromagnets" it stays at (nearly) at the full saturate value as long as $\vec{H}$ doesn't become too large. That's your usual permanent magnet. For soft ferromagnets the magnetization goes away at least partially, and that's why you like to use them in transformers and electro magnets, but usually you still cannot use the linear-response approximation.

Varying $\vec{H}$ and the ferromagnetic material was magnetized before leads to a more complicated curve $\vec{M}=\vec{M}(\vec{H})$ with $\vec{M}(0) \neq 0$. This is called the "hysteresis loop". A very nice phenomomenological explanation for this behavior using semiclassical arguments can be found in the excellent textbook

J. Schwinger, Classical Electromagnetism

Of course if you make the $\vec{H}$ field strong enough you can demagnetized the material of flip the magnetization to another direction. At high enough temperatures the material becomes paramagnetic. That's a typical case of a 2nd-order phase transition, which can be phenomenologically described by Ginzburg-Landau theory.

 

[mertcan]

@Charles Link @vanhees71 @jim hardy there is something scratch my mind...in the link https://unlcms.unl.edu/cas/physics/tsymbal/teaching/EM-913/section5-Magnetostatics.pdf and equation 5.73 we can see that magnetic moment or magnetic moment density depends on a kind of current density. I believe it is not the free charge density but what kind of current density is this what results in that current density??

 

[Charles Link]

@Charles Link @vanhees71 @jim hardy there is something scratch my mind...in the link https://unlcms.unl.edu/cas/physics/tsymbal/teaching/EM-913/section5-Magnetostatics.pdf and equation 5.73 we can see that magnetic moment or magnetic moment density depends on a kind of current density. I believe it is not the free charge density but what kind of current density is this what results in that current density??

The current density can be free moving electrical charges, but often times, the magnetic current density given by $\vec{J}_m=\frac{\nabla \times \vec{M}}{\mu_o}$ is the source of the magnetic moment in these equations. The magnetization $\vec{M}$ is the magnetic moment density. When there are gradients in this quantity, magnetic currents $\vec{J}_m$ are the result=(similar to moving electrical charges, but here any electrical charge motion usually consists of bound quantum states). When the magnetization $\vec{M}$ is uniform but encounters a boundary of the magnetic material, the result by Stokes' theorem is a magnetic surface current per unit length given by $\vec{K}_m=\frac{\vec{M} \times \hat{n}}{\mu_o }$. (Here I'm defining $\vec{M}$ by $\vec{B}=\mu_o \vec{H}+\vec{M}$, instead of by $\vec{B}=\mu_o (\vec{H}+\vec{M}')$). $\\$ You might also find this Insights article that I authored of interest: https://www.physicsforums.com/insights/permanent-magnets-ferromagnetism-magnetic-surface-currents/ You might also find in the section "Discuss in the Community" portion of this "link", posts 32 and 33 of some interest. $\\$ Post 32 is a "link" to a posting that appeared on Physics Forums of an interesting homework laboratory on the Curie temperature. Let me provide that "link" here as well: https://www.physicsforums.com/threa...perature-relationship-in-ferromagnets.923380/ You might find the experimental technique and calculations to determine the magnetization $\vec{M}$ of the permanent magnet of considerable interest. $\\$ Post 33 of "Discuss in the Community" mentions some of the complications that arise from the exchange effect, so that these simple linear theories are, in general, not going to be exact, and may be only somewhat good approximations that don't work in all cases.

 

[jim hardy]

Sometimes a picture helps.
This thought experiment leads to those scary looking formulae that describe it.
https://www.physics.wisc.edu/undergrads/courses/phys202fall96/Phys202_Magnetism.html

old jim

 

[Charles Link]

@jim hardy This is all completely consistent with the calculation that says the magnetic surface current per unit length is given by $\vec{K}_m=\frac{\vec{M} \times \hat{n} }{\mu_o}$. A very good "link" indeed. $\\$ For the illustration, I like to consider a square-shaped small current loop, so that it clearly cancels the current of the adjacent loop.

 

[mertcan]

The current density can be free moving electrical charges, but often times, the magnetic current density given by $\vec{J}_m=\frac{\nabla \times \vec{M}}{\mu_o}$ is the source of the magnetic moment in these equations. The magnetization $\vec{M}$ is the magnetic moment density. When there are gradients in this quantity, magnetic currents $\vec{J}_m$ are the result=(similar to moving electrical charges, but here any electrical charge motion usually consists of bound quantum states). When the magnetization $\vec{M}$ is uniform but encounters a boundary of the magnetic material, the result by Stokes' theorem is a magnetic surface current per unit length given by $\vec{K}_m=\frac{\vec{M} \times \hat{n}}{\mu_o }$. (Here I'm defining $\vec{M}$ by $\vec{B}=\mu_o \vec{H}+\vec{M}$, instead of by $\vec{B}=\mu_o (\vec{H}+\vec{M}')$). $\\$ You might also find this Insights article that I authored of interest: https://www.physicsforums.com/insights/permanent-magnets-ferromagnetism-magnetic-surface-currents/ You might also find in the section "Discuss in the Community" portion of this "link", posts 32 and 33 of some interest. $\\$ Post 32 is a "link" to a posting that appeared on Physics Forums of an interesting homework laboratory on the Curie temperature. Let me provide that "link" here as well: https://www.physicsforums.com/threa...perature-relationship-in-ferromagnets.923380/ You might find the experimental technique and calculations to determine the magnetization $\vec{M}$ of the permanent magnet of considerable interest. $\\$ Post 33 of "Discuss in the Community" mentions some of the complications that arise from the exchange effect, so that these simple linear theories are, in general, not going to be exact, and may be only somewhat good approximations that don't work in all cases.

@Charles Link as far as I have observed in your links and @jim hardy links and my own search, the current density I mentioned at post 40 in given link and equation which affect the magnetic moment density is the circular current around proton or nucleus. Am I right??

I am asking to understand the model of permanent magnets deeply

 

[Charles Link]

@Charles Link as far as I have observed in your link and my own search, the current density I mentioned at post 40 in given links and equation which affect the magnetic moment density is the circular current around proton or nucleus. Am I right

The magnetization $\vec{M}$ , (vector sum of the magnetic moments per unit volume), can actually be due to spin magnetic moment rather than than orbital angular momentum, and I believe that is what happens in the case of iron. $\\$ In the case of spin, the magnetic moment is $\vec{\mu}_s=\frac{g_s \, \mu_B \, \vec{S}}{\hbar}$ , where $\mu_B$ is the Bohr magneton. $\\$ In c.g.s. units, the Bohr magneton $\mu_B=\frac{e \hbar}{2 m_e c }$. $\\$ The constant $g_s \approx 2.0$, and results from the Dirac equation that are beyond my level of expertise give a result that $g_s =2.0032...$ $\\$ For the orbital angular momentum, for which classical models of current loops apply, (with an electron in orbit about the nucleus, etc.), $\vec{\mu}_L=\frac{g_L \, \mu_B \, \vec{L}}{\hbar}$, with $g_L=1.000$. $\\$ The equation $\vec{J}_m=\frac{\nabla \times \vec{M}}{\mu_o}$, and a related equation $\vec{A}(\vec{r})=\frac{\mu_o}{4 \pi} \int \frac{\vec{J}(\vec{r}')}{|\vec{r}-\vec{r}'|} \, d^3 \vec{r}'$, still apply, regardless of the origin of the magnetization.

 

[jim hardy]

For the illustration, I like to consider a square-shaped small current loop, so that it clearly cancels the current of the adjacent loop.

You are not alone. I found a lot of those before finding that circular one.
http://farside.ph.utexas.edu/teaching/302l/lectures/node77.html

I like the round ones because i think of atoms as round and electron orbits as circles - that's all.

old jim

 

[mertcan]

The magnetization $\vec{M}$ , (vector sum of the magnetic moments per unit volume), can actually be due to spin magnetic moment rather than than orbital angular momentum, and I believe that is what happens in the case of iron. $\\$ In the case of spin, the magnetic moment is $\vec{\mu}_s=\frac{g_s \, \mu_B \, \vec{S}}{\hbar}$ , where $\mu_B$ is the Bohr magneton. $\\$ In c.g.s. units, the Bohr magneton $\mu_B=\frac{e \hbar}{2 m_e c }$. $\\$ The constant $g_s \approx 2.0$, and results from the Dirac equation that are beyond my level of expertise give a result that $g_s =2.0032...$ $\\$ For the orbital angular momentum, for which classical models of current loops apply, (with an electron in orbit about the nucleus, etc.), $\vec{\mu}_L=\frac{g_L \, \mu_B \, \vec{L}}{\hbar}$, with $g_L=1.000$. $\\$ The equation $\vec{J}_m=\frac{\nabla \times \vec{M}}{\mu_o}$, and a related equation $\vec{A}(\vec{r})=\frac{\mu_o}{4 \pi} \int \frac{\vec{J}(\vec{r}')}{|\vec{r}-\vec{r}'|} \, d^3 \vec{r}'$, still apply, regardless of the origin of the magnetization.

You are not alone. I found a lot of those before finding that circular one.
http://farside.ph.utexas.edu/teaching/302l/lectures/node77.html

View attachment 225059

I like the round ones because i think of atoms as round and electron orbits as circles - that's all.

old jim

Another interesting question gentlemen : Let's think that we put the iron in a steady state magnetic field environment and we know that iron is going to behave like magnet, points in iron are going to have different pole strength at the end, but HOW MUCH time is required for a given specific point in iron to reach its steady magnetic field at the end?? Can we calculate that situation??
Also until reaching the steady magnetic field at the end, while time passes HOW does the magnitude of specific point's magnetic field change?? Can we calculate also that situation??

 

[Charles Link]

Another interesting question gentlemen : Let's think that we put the iron in a steady state magnetic field environment and we know that iron is going to behave like magnet, points in iron are going to have different pole strength at the end, but HOW MUCH time is required for a given specific point in iron to reach its steady magnetic field at the end?? Can we calculate that situation??
Also until reaching the steady magnetic field at the end, while time passes HOW does the magnitude of specific point's magnetic field change?? Can we calculate also that situation??

@mertcan This is basically a frequency response question, and in post 20, @jim hardy actually showed some examples of frequency response with and without laminations, where the laminated iron layers have better frequency response because it doesn't have the Faraday EMF's and eddy currents to contend with, with their effect increasing with increasing frequency. $\\$ The question you are asking I think could basically be answered by knowing the amount of phase shift that occurs between the primary and secondary. The experiment might be a little complicated by the items mentioned in post 16. In any case, I don't really know what type of frequency response might be expected.

 

[jim hardy]

A lot goes on in a simple piece of iron. I don't think you can write a general equation. From Sylvanus Thompson's 1896 edition of "Dynamo Electric Machinery"

oops sorry for overlapping snips.

I have an original 1901 edition and it's a delight .
Your question would i think be best answered by experiment on a specimen of the particular alloy, heat-treatment, shape, size, temperature, and recent magnetization that interests you.

A search on phrase "sylvanus thompson retardation of magentization" also turns up the 1903 edition of his book "Design of Dynamos" with some similar paragraphs. Some of his books are reprinted in India, to the credit of educators there. You might find one an interesting addition to your library.

old jim

 

[jim hardy]

in post 20, @jim hardy actually showed some examples of frequency response with and without laminations,

Actually the three images in post #20 are the same non-laminated core at three different frequencies 3hz 10hz and 60 hz. That core was hopeless at 60 hz.