kosmocomet
- 11
- 0
Homework Statement
Homework Equations
- m=N*I*A
- T=m X B
- m = n(unit vector) *m
The Attempt at a Solution
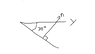
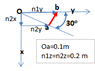
To calculate m, I know it is just plugging in the information. Thus, m=0.8. Now, the question is computing the unit vector, which has me confused. Using the right hand rule, and going along the current, The normal should look something like this, correct:
If so, how do I make this into an x(unit) and y(unit)?
Any help is much appreciated!