AladdinSane
- 8
- 0
Homework Statement
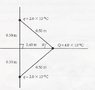
Two equal positive charges, both q = 2.0 x 10^ -6 C, interact with a third charge Q = 4.0 x 10^ -6 C, as shown above. What is the magnitude of the electric force on Q?[/B][/B]
Homework Equations
Electric force = Kc (q1/r^2)
The Attempt at a Solution
Basically, I believe that my problem is in solving the vectors.
I attempted to break down the charges(it is hard to show this work on here but...) I broke it down into...
E(y) = E(1) x sin Θ(1) + E(2) x sin Θ(2)
E(x) = E(1) x cox Θ(1) - E(2) sin Θ(2)
I'm not sure if that makes sense, but it was all I could think of...Any help would be greatly appreciated. Thanks a lot!