Houdini176
- 18
- 0
Homework Statement
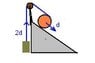
A solid cylinder of weight 50 lb (mass=2.3 kg) and radius 3.0 in (7.6 cm) has a light thin tape wound around it. The tape passes over a light, smoother fixed pulley to a 10-lb (mass=4.5 kg) body, hanging vertically. If the plane on which the cylinder moves is inclined 30 degrees to the horizontal, find a) the linear acceleration of the cylinder down the incline and b) the tension in the tape, assuming no slipping.
Homework Equations
I thought I knew how to do this using a conservation of energy approach, but my answers don't match up. I'm also not sure how to do this dynamically. When I try dynamically, the torque created by friction = (ma)/2. I'm not sure how to treat this, does the "a" refer to the overall linear acceleration (or, the linear acceleration of the center of mass) of the body or just the linear acceleration imparted by the frictional force? In another example in this book, when the only torque on the cylinder was friction, the "a" from friction=(ma)/2 and the overall linear acceleration were treated as if they were the same. How should I treat it (friction) and other torques, particularly the acceleration they impart on the body? Also, could someone tell me what I'm doing wrong (see below)? Thanks.
The Attempt at a Solution
MGHc=(MV^2)/2+(Iw^2)/2+MbGHb
MGHc=(MV^2)/2+(MV^2)/4+MbGHb
MGHc=3(MV^2)/4+MbGHb
I'm not so sure about this part, but because there is no slipping, the block should be "reeled in" in by cylinder's rotation as much as it is pulled upward from the cylinder's linear motion. So, Hb=2d and Hc=sin(30)d, where d is the linear distance the cylinder travels along the ramp.
M*G*sin(30)*d=3(MV^2)/4+2MbGd
M*G*sin(30)*d-2*Mb*G*d=3(MV^2)/4
4*G*d*(M*sin(30)-2(Mb))/(3M)=V^2=2ad
a=2*g*(M*sin(30)-2(Mb))/(3M)=0.71 m/2^s, but the answer is 0.47 m/s^2
Last edited: