helium4amc
- 3
- 0
I'm sure I must be being a bit dim here, but I can't work this out!
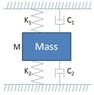
I have a mass-spring-damper system, as shown in the attahed picture, in which i have a mass suspended between two springs and dampers, each of which are attached to a fixed surface. he two opposite surfaces are part of the same fixed mass (i.e. the whole thing is inside a rigid box).
I know that a normal system with a single spring and damper can be expressed (in the Laplace domain) as
k / (k + Cs + ms^2)
But I can't work out how to modify the equation to include the mass and spring on the other side!
Any advice would be most welcome!
Thanks,
Andrew
I have a mass-spring-damper system, as shown in the attahed picture, in which i have a mass suspended between two springs and dampers, each of which are attached to a fixed surface. he two opposite surfaces are part of the same fixed mass (i.e. the whole thing is inside a rigid box).
I know that a normal system with a single spring and damper can be expressed (in the Laplace domain) as
k / (k + Cs + ms^2)
But I can't work out how to modify the equation to include the mass and spring on the other side!
Any advice would be most welcome!
Thanks,
Andrew