Challenge Math Challenge - March 2020

[fresh_42]

Questions

1. (solved by @Antarres, @Not anonymous ) Prove the inequality $\cos(\theta)^p\leq\cos(p\theta)$ for $0\leq\theta\leq\pi/2$ and $0<p<1$. (IR)

2. (solved by @suremarc ) Let $F:\mathbb{R}^n\to\mathbb{R}^n$ be a continuous function such that $||F(x)-F(y)||\geq ||x-y||$ for all $x,y\in\mathbb{R}^n$. Show that $F$ is a homeomorphism. (IR)

3. (solved by @Fred Wright ) Evaluate the integral $\int_0^{\infty}\frac{e^{-t}\sin(t)}{t}dt\,.$ (IR)

4. (solved by @suremarc ) Let $k$ be a field that is not algebraically closed. Let $n\geq 1$. Show that there exists a polynomial $p\in k[x_1,\ldots,x_n]$ that vanishes only at the origin $(0,\ldots,0)\in k^n$. (IR)

5. (solved by @Not anonymous ) Find the area of the shape $T$ which is surrounded by the line $|a_1 x + b_1 y + c_1| + |a_2 x + b_2 y + c_2| = m , m \gt 0$ (given that $a_1 b_2 - a_2 b_1 \neq 0$). (QQ)

6. (solved by @Antarres ) Calculate $I = \iint\limits_{R^2} e^{-|y|- x^2} dx dy$ (QQ)

7. (solved by @Antarres ) Let's take the vector space of continuous real functions. Let also $g: V \ni f \rightarrow g(f) \in V$ be a linear mapping with $(g(f))(x) = \int_{0}^{x} f(t) dt\,.$ Show that $g$ has no eigenvalues. (QQ)

8. Let $\mathfrak{g}=\operatorname{lin}_\mathbb{R}\{\,e_1,e_2,e_3,e_4\,\}$ on which we define the following multiplication:
$$
[e_1,e_4]=2e_1\; , \;[e_2,e_4]=3e_2-e_3\; , \;[e_3,e_4]=e_2+3e_3
$$
and $[e_i,e_j]=0$ otherwise, as well as $[e_i,e_i]=0$.
Show that
a.) $\mathfrak{g}$ is a Lie algebra.
b.) There exists an $\alpha_0 \in A(\mathfrak{g})$ where $$
A(\mathfrak{g}):=\{\,\alpha : \mathfrak{g}\stackrel{\text{linear}}{\longrightarrow} \mathfrak{g}\,|\,\forall\,X,Y \in \mathfrak{g}: [\alpha(X),Y]+[X,\alpha(Y)]=0\,\}
$$
such that $[\operatorname{ad}X,\alpha_0] \in \mathbb{R}\cdot \alpha_0$ for all $X\in \mathfrak{g}\,.$
c.) The center $Z(\mathfrak{g})=\{\,0\,\}\,.$
d.) $\mathfrak{g}$ has a one dimensional ideal.
(FR)

9. (solved by @suremarc ) Let $A,B\in \mathbb{M}(m,\mathbb{R})$ and $\|A\|,\|B\|\leq 1$ with a submultiplicative matrix norm, then $$\left\|\,e^{A+B}-e^A\cdot e^B\,\right\|\leq 6e^2\cdot \left\|\,[A,B]\,\right\|$$
(FR)

10. (solved by @julian ) Show that for $m \times m$ matrices $A,B$
$$
e^{t\,(A+B)} = \lim_{n \to \infty}\left(e^{t\,\frac{A}{n}} \cdot e^{t\,\frac{B}{n}}\right)^n
$$
in a submultiplicative matrix norm.
Hint: You may use the estimation in problem #9. (FR)

High Schoolers only

11. (solved by @etotheipi, @Not anonymous, @lekh2003 ) If $\tan^2 a = 1 + 2 \tan^2 b$ show that it also holds $\cos 2b - 2 \cos 2a = 1$ (QQ)

12. (solved by @etotheipi ) Inside a steel sphere of radius $R$ we construct a spherical cavity which is tangent to the steel sphere and passes through its center ($Fig. 1$). Before this construction, the mass of the steel sphere was $M$. Find the force $F$ (which is due to the Newton's law of gravitation) with which the steel sphere pulls a small sphere of mass $m$ which is at a distance $d$ from its center over the straight line of centers and on the side of the cavity.

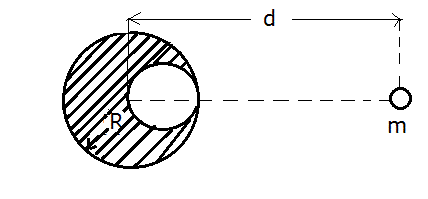
$Fig. 1$

Now, I think this way: I find the center of gravity of the sphere with the cavity: its distance from the center of the sphere I would have without constructing the cavity (i.e. concrete sphere), can be found from the equation $Mgx = \frac{Mg}{8} (\frac{R}{2} + x)$ from which I find $x = \frac{R}{14}$. Then, I find the force $F$ which is exerted on the sphere of mass $m$ by the sphere with the cavity (its mass is the $\frac{7}{8}$ of the mass of the concrete steel sphere), like we had two spheres with a distance $d + \frac{R}{14}$ between them, so $F = G\frac{\frac{8}{7}Mm}{(d + \frac{R}{14})^2}$.

Is this correct? Try to recreate the solution in detail and justify your answer. If the above solution is not correct, give your solution. (QQ)

13. (solved by @Not anonymous ) Let $f:\mathbb{Q}\to\mathbb{Q}$ be the function $f(x)=x^3-2x$. Show that $f$ is injective. (IR)

14. (solved by @Not anonymous, @krns21 ) Given two integers $n,m$ with $nm\neq 0$. Show that there is a integer expression $1=sn+tm$ if and only if $n$ and $m$ are coprime, i.e. have no proper common divisor. (FR)

15. (solved by @Not anonymous ) Division of an integer by a prime number $p$ leaves us with the possible remainders $C:=\{\,0,1,2,\ldots ,p-1\,\}\,.$ We can define an addition and a multiplication on $C$ if we wrap it around $p$, i.e. we identify $0=p=2p=3p= \ldots \, , \,1=1+p=1+2p=1+3p=\ldots\, , \,\ldots$ This is called modular arithmetic (modulo $p$).

Show that for any given numbers $a,b\in C$ the equations $a+x=b$ and $a\cdot x =b$ ($a\neq 0$) have a unique solution.
Is this still true if we drop the requirement that $p$ is prime? (FR)

Remark: This problem is about proof techniques, so be as accurate (not long) as possible, i.e. note which property or condition you use at each step.

 

[krns21]

14. Given two integers $n,m$ with $nm\neq 0$. Show that there is a integer expression $1=sn+tm$ if and only if $n$ and $m$ are coprime, i.e. have no proper common divisor. (FR)

Spoiler: Problem 14

Let gcd$(n,m)=a$
Therefore:
$n=aq$ for some integer $q$
$m=ap$ for some integer $p$
Substituting $aq$ and $aq$ for $n$ and $m$ to the expression $1= sn + tm$, we see that:
$1 =saq + tap$
$1 = a(sq+tp)$
Since all are integers, $sq+tp$ must also be an integer. Therefore, $a=1$.
If $a > 1$, then this expression has no integer solutions for any $s,q,tp$. It's easier seen in this form:
$\frac{1}{a} = sq +tp$
The left hand side of this expression is a fraction whilst the right hand side is integer and so there is a contradiction.

 

[fresh_42]

Spoiler: Problem 14

Let gcd$(n,m)=a$
Therefore:
$n=aq$ for some integer $q$
$m=ap$ for some integer $p$
Substituting $aq$ and $aq$ for $n$ and $m$ to the expression $1= sn + tm$, we see that:
$1 =saq + tap$
$1 = a(sq+tp)$
Since all are integers, $sq+tp$ must also be an integer. Therefore, $a=1$.
If $a > 1$, then this expression has no integer solutions for any $s,q,tp$. It's easier seen in this form:
$\frac{1}{a} = sq +tp$
The left hand side of this expression is a fraction whilst the right hand side is integer and so there is a contradiction.

You have shown, that if we have such an expression, then $n$ and $m$ are coprime:
$1=sn+tm \,\wedge \, a|n \,\wedge \, a|m \Longrightarrow a=1$

Your second argument says $a >1 \,\wedge \, a|n \,\wedge \, a|m\Longrightarrow 1\neq sn+tm$ which is equivalent to the first.

However, if we assume $(n,m)=1$, then you must show that $s$ and $t$ exist with $1=sn+tm\,.$

 

[fresh_42]

Spoiler: Problem 14

Let gcd$(n,m)=a$
Therefore:
$n=aq$ for some integer $q$
$m=ap$ for some integer $p$
Substituting $aq$ and $aq$ for $n$ and $m$ to the expression $1= sn + tm$, we see that:
$1 =saq + tap$
$1 = a(sq+tp)$
Since all are integers, $sq+tp$ must also be an integer. Therefore, $a=1$.
If $a > 1$, then this expression has no integer solutions for any $s,q,tp$. It's easier seen in this form:
$\frac{1}{a} = sq +tp$
The left hand side of this expression is a fraction whilst the right hand side is integer and so there is a contradiction.

A hint: You could consider all natural numbers $x=sn+tm$ and consider what you can find out about the smallest of them.

 

[krns21]

A hint: You could consider all natural numbers $x=sn+tm$ and consider what you can find out about the smallest of them.

Spoiler

Bezout's identity?

 

[krns21]

For Problem 15, if both $a= 0$ and $b= 0$, then $a \cdot x = b$ doesn't have a unique solution.

 

[fresh_42]

For Problem 15, if both $a= 0$ and $b= 0$, then $a \cdot x = b$ doesn't have a unique solution.

Thanks for the hint. Yes, $a\neq 0$ has to be added to the question. I corrected it.

 

[fresh_42]

Spoiler

Bezout's identity?

Yes, but how to prove it? Consider the smallest integer number $x=sn+tm > 0$ and take $1= \operatorname{gcd}(n,m)$. Why is $x=1$?

 

[etotheipi]

Spoiler: Problem 11

$\tan^{2}{(a)} = 1+ 2\tan^{2}{(b)}$
$\sec^{2}{(a)} - 1 = 1+ 2\sec^{2}{(b)} -2 = 2\sec^{2}{(b)} - 1$
$\cos^{2}{(a)} = \frac{1}{2} \cos^{2}{(b)}$
$\frac{\cos{(2a)}+1}{2} = \frac{1}{2} \times \frac{\cos{(2b)}+1}{2}$
$2\cos{(2a)} + 2 = \cos{(2b)}+1 \implies \cos{(2b)} - 2\cos{(2a)} = 1$

 

[etotheipi]

Spoiler: Problem 12

The force on $m$ due to the whole large sphere without the cavity, $F_T$ can be considered as the sum of the forces due to the large sphere with the cavity, $F_C$, and the force due to a spherical mass which fills the cavity, $F_M$, by the principle of superposition.

So $F_C = F_T - F_M$

The force that would result from the whole large sphere without a cavity is $F_T = \frac{GMm}{d^2}$. The force that would result from the spherical mass taking the place of the cavity is $F_M = \frac{GMm}{8(d-\frac{R}{2})^{2}}$.

So $F_C = GMm[\frac{1}{d^{2}} - \frac{1}{8(d-\frac{R}{2})^{2}}]$

For the second part, I think the error lies in abstracting the mass with the cavity to a sphere because the spatial distribution of mass will affect the resulting field.

 

[Not anonymous]

11. If $\tan^2 a = 1 + 2 \tan^2 b$ show that it also holds $\cos 2b - 2 \cos 2a = 1$ (QQ)

Spoiler: Question 11

The proof uses the following identities:
1. $\cos (x+y) = \cos x \cos y - \sin x \sin y \Rightarrow \cos {2A} = \cos {(A+A)} = \cos^2 A - \sin^2 A = 2 \cos^2 A - 1$

2. $\tan x = \frac {\sin x} {\cos x}$

3. $\sin^2 x = 1 - \cos^2 x$

The given equality, $\tan^2 a = 1 + 2 \tan^2 b$, can be rewritten in terms of sine and cosine:
$$
\frac {\sin^2 a} {\cos^2 a} = 1 + 2 \frac {\sin^2 b} {\cos^2 b} \Rightarrow \frac {1} {\cos^2 a} - 1 = 1 + 2 (\frac {1} {\cos^2 b} - 1) \Rightarrow {\cos^2 a} = \frac {\cos^2 b} {2}
$$

Multiplying both sides by 4 and subtracting 2 from both, we get:
$4 \cos^2 a - 2 = 2 \cos^2 b - 2 \Rightarrow 2 (2 \cos^2 a - 1) = (2 \cos^2 b - 1) - 1$

Using the identity for $\cos 2A$ on both sides, the equation becomes
$2 \cos 2a = \cos 2b - 1 \Rightarrow \cos 2b - 2 \cos 2a = 1$, hence proving what is required

 

[lekh2003]

Spoiler: Problem 11

\begin{align*}

\tan^2a &= 1 + 2\tan^2b\\
\tan^2a &= \sec^2b + \tan^2b\\
\cos^2b \tan^2a &= 1 + \sin^2b\\
\cos^2b \tan^2a &= 2 - \cos^2b\\
\cos^2b \sin^2a &= 2\cos^2a - \cos^2b\cos^2a\\
\cos^2b(\sin^2a+\cos^2a) &= 2\cos^2a\\
\cos^2b &= 2\cos^2a\\
\cos^2b &= \cos2a + 1\\
2\cos^2b &= 2\cos2a + 2\\
\cos2b &= 2\cos2a + 1 \\
\implies \cos2b &- 2\cos2a = 1
\end{align*}

Just realized this one was super solved but I'm not going to let this LaTeX go to waste :p

 

[Fred Wright]

Problem #3
I use Feynman's famous trick of differentiation under the integral sign.

Spoiler

$$
\frac {d}{d \alpha} \int_{0}^{ \infty } \frac{e^{-\alpha t}\sin (t)}{t}dt=- \int_{0}^{ \infty }e^{-\alpha t}\sin (t)dt
$$
Integrating by parts:
$$
- \int_{0}^{ \infty }e^{-\alpha t}\sin (t)dt= \frac {1}{\alpha^2 + 1}
$$
taking the antiderivative of $\frac {1}{\alpha^2 + 1}$ :
$$
\int_{0}^{ \infty } \frac{e^{-\alpha t}\sin (t)}{t}dt= atan(\alpha) + C
$$
Setting $\alpha = 0$ to find $C$ :
$$
C= \int_{0}^{ \infty }\frac{\sin (t)}{t}dt
$$
I observe:
$$
\int_{0}^{ \infty }e^{-xt}dt=\frac{1}{x}
$$
and thus (again integrating by parts):
$$
C= \int_{0}^{ \infty }\frac{\sin (t)}{t}dt= \int_{0}^{ \infty } \int_{0}^{ \infty }e^{-xt}\sin (x)dxdt=\int_{0}^{ \infty }\frac{dt}{t^2 + 1}=\frac{\pi}{2}
$$
and finally,
$$
\int_{0}^{ \infty } \frac{e^{- t}\sin (t)}{t}dt= atan(1) + \frac{\pi}{2} = \frac{3 \pi}{4}
$$

 

[lekh2003]

Spoiler: Problem 13

I think I'm far from solving the problem, but I made some progress. I let $$a,b,c,d \in \mathbb{Z}$$ and hence I need to prove $$f\left(\frac{a}{b}\right) = f\left(\frac{c}{d}\right) \implies \frac{a}{b} = \frac{c}{d} \text{ or } ad = bc$$

I managed to simplify this form all the way into:

$$
(ad-bc)((ad)^2 + adbc + (bc)^2) = 2b^2d^2 (ad-bc)
$$

All I need to show now is really that: $$((ad)^2 + adbc + (bc)^2) = 2b^2d^2$$

I'll keep at it.

 

[Infrared]

@Fred Wright Nice work! Your solution is totally correct except for a lost negative sign: $\int_0^{\infty}\frac{e^{-\alpha t}\sin(t)}{t}dt=-\arctan(\alpha)+C.$

So the answer should be $-\pi/4+\pi/2=\pi/4$ instead.

Also, a slightly easier way to find $C$ is to take $\alpha\to\infty.$

 

[QuantumQuest]

Just realized this one was super solved but I'm not going to let this LaTeX go to waste :p

Your solution is correct but you need to correct the latex because at some points there are typos.

 

[lekh2003]

Your solution is correct but you need to correct the latex because at some points there are typos.

Ohhh yeah, I'll do that, thx.

 

[Not anonymous]

14. Given two integers $n,m$ with $nm\neq 0$. Show that there is a integer expression $1=sn+tm$ if and only if $n$ and $m$ are coprime, i.e. have no proper common divisor. (FR)

Spoiler: Question 14

First we prove by contradiction that if $n,m$ are not coprime, then an integer expression of the mentioned form cannot exist. If $n, m$ are not coprime, they must have a GCD $k \gt 1$. $n, m$ can therefore be written as multiples of $k$ with integer quotients, say $a, b$ respectively. Suppose there existed an integers only solution for $1=sn+tm$, then writing $n,m$ in terms of $k$, we get:
$sak + tbk = 1 \Rightarrow k(sa+tb) = 1 \Rightarrow (sa + tb) = \frac 1 k$.
However, since $k \gt 1$, $\frac 1 k$ cannot be an integer and this contradicts the assumption that $s, t, a, b$ are all integers. Hence, such an expression cannot exist for non-coprime numbers $n,m$.

Next we prove that if $n,m$ are coprime, then an integer expression of the form $1=sn+tm$ must exist. For simplicity, we prove this assuming $n,m$ are positive integers. Once that is proved, it is easy to show that a similar expression would exist if negatives of one or both of $n,m$ are used instead. Since if there exist integers $s,t$ such that $sn+tm=1$, then if $n$ is negated (replaced by $-n$), then we simply need to replace $s$ by $-s$ and similarly replace $t$ by $-t$ if $m$ is negated to get the same value for the expression and therefore the existence of an integer-only solution still holds true.

Proof for the case of positive coprime integers $n, m$ is as follows. Since $LCD(n,m) = nm$, $kn \mod m \neq 0$ for any $k \in \{1, 2, ..., m-1\}$. There must exist a $k \in \{1, 2, ..., m-1\}$ for which $kn \mod m = 1$. Suppose there existed no such value of $k$, then the list of $m-1$ values, $(n \mod m, 2n \mod m, 3n \mod m, ..., (m-1)n \mod m)$ must have at least one repeated integer value $p, 1 \lt p \lt m$ (since the list has $(m-1)$ elements and modulo w.r.t. m can only take values from $\{0, 1, .., (m-1)\}$ and 0, 1 have been ruled out as possible values, leaving only $(m-2)$ values to choose from for the $(m-1)$ elements, there must be a repetition). Suppose $k_1, k_2$ (assume $k_1 \lt k_2$) were 2 of the different values of $k$ for which $kn \mod m = p$, then $k_2 n - k_1 n = 0 \mod m \Rightarrow (k_2 - k_1)n = 0 mod m$ and since $1 \leq k_2 - k_1 \lt (m-1)$, this contradicts the requirement that $kn \mod m \neq 0$ for any $k \in \{1, 2, ..., m-1\}$. Hence it is proven that there exists a $k \in \{1, 2, ..., m-1\}$ for which $kn \mod m = 1$. Now, for that value of $k$, we must have $kn = qm +1$ for some integer $q \geq 1$. Hence the expression $kn + (-q)m$ must have the value 1, therefore we have an integer expression $1 = sn + tm$ that is true with $s = k$ and $t = q$. Hence proven.

 

[hilbert2]

For problem 1:

Spoiler

First of all, it's known that

$1-\frac{1}{2}\theta^2 \leq \cos \theta \leq 1-\frac{1}{2}\theta^2 +\frac{1}{24}\theta^4$

and

$1-\frac{1}{2}p^2 \theta^2 \leq \cos p\theta \leq 1-\frac{1}{2}p^2 \theta^2 +\frac{1}{24}p^4 \theta^4$

when $\theta\in [0,\pi /2]$.

Then, if we could show that

$(\cos \theta)^p \leq \left(1-\frac{1}{2}\theta^2 +\frac{1}{24}\theta^4 \right)^p \leq \left(1-\frac{1}{2}p^2 \theta^2\right) \leq \cos p\theta$,

or most importantly, the part

$\left(1-\frac{1}{2}\theta^2 +\frac{1}{24}\theta^4 \right)^p \leq \left(1-\frac{1}{2}p^2 \theta^2\right)$

for $\theta\in ]0 ,\pi/2[$ and $p\in [0,1]$,

then it would prove the claim.

Drawing graphs of the functions $f(\theta) = \left(1-\frac{1}{2}\theta^2 +\frac{1}{24}\theta^4 \right)^p$ and $g(\theta )=\left(1-\frac{1}{2}p^2 \theta^2\right)$ it seems that $f(x)\leq g(x)$ on that interval no matter how small number the $p$ is, but I'm not sure how to actually prove it.

Assuming that $p$ is the reciprocal of an integer: $p = 1/n$ with $n\in\mathbb{N}$, it may be possible to prove this for any $n\in\mathbb{N}$ with mathematical induction.

 

[Antarres]

Spoiler: Question #1

Take the function : $f(\theta) = \cos(p\theta) - \cos^p(\theta)$.
We find the first derivative:
$$f'(\theta) = -p\sin(p\theta) + p\cos^{p-1}(\theta)\sin(\theta)$$
We want to check that $f'$ is nonnegative(because $f(0)=0$), which makes our function increasing on the interval $0\leq\theta\leq \frac{\pi}{2}$, for $0<p<1$.
In order to check this, we analyze the function:
$$g(x) = \cos^{p-1}(\theta)\frac{\sin(\theta)}{\theta}$$
Since $\cos^{p-1}(\theta) = \frac{1}{\cos^{1-p}(\theta)}$ is an increasing function, as a composition of two decreasing functions(cosine is decreasing in the first quadrant), this means that $\cos^{p-1}(\theta) \geq 1$ for $0\leq\theta\leq\tfrac{\pi}{2}$, and hence $g(\theta) \geq 1$ on this interval, since $\frac{\sin(x)}{x}$ is positive on this interval.
Then we have:
$$g(\theta) \geq 1 >p \Rightarrow \cos^{p-1}(\theta)\sin(\theta) > p\theta \geq \sin(p\theta)$$
where in the last inequality we used the known relation $\sin(x) \leq x$ that holds for all $x$.
But then this means that $f'(\theta) >0$, by multiplying the above inequality by $p$. Hence, $f$ is increasing.
For $\theta = 0$, we have $f(0) = 0$, so the function is positive on this interval. So we have:
$$f(\theta) \geq 0 \Rightarrow \cos(p\theta) \geq \cos^p(\theta)$$
This finishes the proof.

 

[Antarres]

This sounds kind of simple, since the integrals are separated...or am I missing something?

Spoiler: Question #6

Denote:
$$I = \iint_{R^2} e^{-\vert y\vert -x^2}dxdy = \int_{-\infty}^{\infty} e^{-\vert y\vert}dy \int_{-\infty}^{\infty} e^{-x^2}dx$$
We solve the integrals separately:
$$\int_{-\infty}^{\infty} e^{-\vert y\vert}dy = 2 \int_0^{\infty} e^{-y}dy =2$$
$$\int_{-\infty}^{\infty} e^{-x^2}dx = \sqrt{\pi}$$

The second integral is Gaussian integral, which can be integrated as follows:
$$ \left(\int_{-\infty}^{\infty} e^{-x^2}dx\right)^2 = \left(\int_{-\infty}^{\infty} e^{-x^2}dx\right)\left(\int_{-\infty}^{\infty} e^{-y^2}dy\right) \equiv I_G^2$$
Switching to polar coordinates, we find:
$$I_G^2 = 2\pi \int_{0}^{\infty} e^{-r^2}rdr = \pi\int_{0}^{\infty} e^{-r^2} d(r^2) = \pi$$
Hence: $I_G = \sqrt{\pi}$
So finally, we find: $I = 2\sqrt{\pi}$

 

[Antarres]

Spoiler: Question #7

We have from definition of $g$, that if $F$ is a primitive function of $f$:
$$g(f) = F \qquad F'(x) = f(x)$$
by fundamental theorem of calculus.
Then, the eigenvalue equation for $g$ is:
$$g(f) = \lambda f$$
for some $\lambda \in \mathbb{R}$. Substituting the first equation into this, we have:
$$F(x) = \lambda F'(x)$$
with $F(0)=0$.
The general solution of this equation is proportional to the exponential function(obtained by separation of variables):
$$F(x) = Ae^{\lambda x}$$
with $A$ being the integration constant. However, the initial condition cannot be satisfied for this function, hence there are no solutions to the initial value problem and so for the eigenvalue problem either.
QED

 

[Infrared]

Since $\cos^{p-1}(\theta) = \frac{1}{\cos^{1-p}(\theta)}$ is an increasing function, as a composition of two decreasing functions(cosine is decreasing in the first quadrant), this means that $\cos^{p-1}(\theta) \geq 1$ for $0\leq\theta\leq\tfrac{\pi}{2}$, and hence $g(\theta) \geq 1$ on this interval, since $\frac{\sin(x)}{x}$ is positive on this interval.

I don't see how you are concluding that $g(\theta)\geq 1$. I agree that $\cos^{p-1}(\theta) \geq 1$ but $\frac{\sin\theta}{\theta}$ is less than one.

Anyway, there is a more direct way to get the result from your expression for $f'(\theta)$.

 

[archaic]

Question 1:

Spoiler

$$\begin{align*}
\frac{d}{dx}\left(\cos(px)-\cos^px\right)&=-p\sin(px)+p\sin x\cos^{p-1}x\\
&=p\left(\sin x\cos^{p-1}x-\sin(px)\right)\\
&=p\left(\sum_{k=0}^\infty\frac{(-1)^k\cos^{p-1}x}{(2k+1)!}x^{2k+1}-\sum_{k=0}^\infty\frac{(-1)^k p^{2k+1}}{(2k+1)!}x^{2k+1}\right)\\
&=p\sum_{k=0}^\infty\left(\frac{(-1)^k}{(2k+1)!}x^{2k+1}\left(\cos^{p-1}x-p^{2k+1}\right)\right)\\
&=p\left(\cos^{p-1}x-p\right)x-\frac{p}{3!}\left(\cos^{p-1}x-p^3\right)x^3+\frac{p}{5!}\left(\cos^{p-1}x-p^5\right)x^5+...
\end{align*}$$
Each $-$ operation yields a positive result as long as the coefficients are positive, but I need to prove that.

 

[Infrared]

$$=p\left(\cos^{p-1}x-p\right)x-\frac{p}{3!}\left(\cos^{p-1}x-p^3\right)x^3+\frac{p}{5!}\left(\cos^{p-1}x-p^5\right)x^5+...$$

Can you explain in some more detail why this sum is nonnegative?

 

[archaic]

Can you explain in some more detail why this sum is nonnegative?

I answered too fast

 

[Antarres]

@Infrared You're right, I don't know why I complicated such a simple thing.

Spoiler: Question #1 - derivative non-negativity proof

We take the form of the derivative $f'(\theta)$:
$$f'(\theta) = p(\cos^{p-1}(\theta)\sin(\theta) - \sin(p\theta))$$
Now we remember that sine is an increasing function in the first quadrant, while cosine is a decreasing one. This means that $\cos^{p-1}(\theta) = \tfrac{1}{\cos^{1-p}(\theta)}$ is an increasing function as a composition of two decreasing functions. Then we have the inequalities(keeping in mind $0<p<1$):
$$\sin(p\theta) \leq \sin(\theta) \qquad \cos^{p-1}(\theta)\geq \cos^{p-1}(0) = 1$$
Substituting into the derivative, we find:
$$f(\theta) \geq p\sin(\theta)(\cos^{p-1}(\theta)-1) \geq p\sin(\theta) \geq 0$$
Hence the derivative is nonnegative and $f$ is monotonously increasing as claimed.

 

[archaic]

13. Let $f:\mathbb{Q}\to\mathbb{Q}$ be the function$f(x)=x^3-2x$. Show that $f$ is injective. (IR)

Incomplete attempt:

Spoiler

Let $p/q$ and $r/s$ be in $\mathbb{Q}$ such that $f(p/q)=f(r/s)$.
$$\begin{align*}
f\left(\frac{p}{q}\right)=f\left(\frac{r}{s}\right)&\Leftrightarrow\left(\frac{p}{q}\right)^3-2\frac{p}{q}=\left(\frac{r}{s}\right)^3-2\frac{r}{s}\\
&\Leftrightarrow \left(\frac{p}{q}\right)^3-\left(\frac{r}{s}\right)^3-2\left(\frac{p}{q}-\frac{r}{s}\right)=0\\
&\Leftrightarrow\left(\frac{p}{q}-\frac{r}{s}\right)\left(\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2\right)-2\left(\frac{p}{q}-\frac{r}{s}\right)=0\\
&\Leftrightarrow\left(\frac{p}{q}-\frac{r}{s}\right)\left(\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2-2\right)=0\\
\end{align*}$$
$$\frac{p}{q}=\frac{r}{s}\text{ or }\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2=2$$
$$\begin{align*}
\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2=2&\Leftrightarrow\left(\frac{p}{q}+\frac{r}{s}\right)^2-\frac{p}{q}\frac{r}{s}=2
\end{align*}$$

 

[BWV]

I am lame at proofs, but could not this be a simpler route to #1?

Spoiler: Spoiler

Take the first three terms of the series expansion:

$cos(n\theta)=1-\frac{n^2\theta ^2}{2}+\frac{n^4\theta ^4}{24}$

$cos(\theta)^n=1-\frac{n\theta ^2}{2}+\frac{1}{24}(3n^2-2n)\theta^4$

as $cos(θ)≥0$ for $0≤θ≤π/2$

for 0<n<1,
$\frac{n^2\theta ^2}{2}<\frac{n\theta ^2}{2}$
(the second negative term for $cos(\theta)^n$ is larger)
and
$\frac{1}{24}(3n^2-2n)\theta^4 <\frac{n^4\theta ^4}{24}$
(the third positive term for $cos(\theta)^n$ is smaller)

 

[Antarres]

@BWV You can't equal the cosine to just a couple of terms of Maclaurin expansion, it's an approximation. And it works for small $\theta$, but here it isn't necessarily small. I think that's the problem with your approach. If you took the whole series, then I don't know how simpler it would be. Or if you made those equalities inequalities. I think it's what archaic and hilbert did in their posts.

Also, the last inequality you provide doesn't work for $0<n<1$.

 

[BWV]

No, the last inequality is good, seems counter-intuitive but (3n^2-2n)<n^4 for 0<n<1
it its also true for n>1 and n<-2

I guess if you could prove every positive term of order n is smaller and every negative term greater for $cos(\theta)^n$ relative to $cos(n\theta)$ that would be valid, but the expansion for $cos(\theta)^n$ is kind of wonky

 

[Antarres]

Oh true, my bad, I drew the function incorrectly. Anyways, what I said stands though, you can't equal cosine to the first three terms in the expansion around zero when the angle can go up to $\frac{\pi}{2}$ radians. You can make an inequality like hilbert did, and go from there.

 

[Infrared]

@Antarres The solution to problem 1 is good!

@BWV Here @Antarres is right. You have to justify why you can throw out all of the higher order terms in the Taylor series.

@archaic You're doing the right type of manipulations. Do you want a hint?

 

[hilbert2]

It's possible that the approach in my post about Problem 1 requires more than 2 or 3 terms in the power series approximations when $p>0.9$. Solving this with the properties of derivatives is certainly a lot easier than using only the polynomial bounds for the trig functions.

 

[QuantumQuest]

This sounds kind of simple, since the integrals are separated...or am I missing something?

Your solution is correct. In order for your solution to be perfect just correct the small typo in the second to last line of your latex.

 

[archaic]

Incomplete attempt:

Spoiler

Let $p/q$ and $r/s$ be in $\mathbb{Q}$ such that $f(p/q)=f(r/s)$.
$$\begin{align*}
f\left(\frac{p}{q}\right)=f\left(\frac{r}{s}\right)&\Leftrightarrow\left(\frac{p}{q}\right)^3-2\frac{p}{q}=\left(\frac{r}{s}\right)^3-2\frac{r}{s}\\
&\Leftrightarrow \left(\frac{p}{q}\right)^3-\left(\frac{r}{s}\right)^3-2\left(\frac{p}{q}-\frac{r}{s}\right)=0\\
&\Leftrightarrow\left(\frac{p}{q}-\frac{r}{s}\right)\left(\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2\right)-2\left(\frac{p}{q}-\frac{r}{s}\right)=0\\
&\Leftrightarrow\left(\frac{p}{q}-\frac{r}{s}\right)\left(\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2-2\right)=0\\
\end{align*}$$
$$\frac{p}{q}=\frac{r}{s}\text{ or }\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2=2$$
$$\begin{align*}
\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2=2&\Leftrightarrow\left(\frac{p}{q}+\frac{r}{s}\right)^2-\frac{p}{q}\frac{r}{s}=2
\end{align*}$$

Spoiler

$$\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2=2\Leftrightarrow (ps)^2+pqrs+(qr)^2=2(qs)^2$$
We will analyse $(ps)^2+pqrs+(qr)^2=2(qs)^2$:
For the LHS to be even, I need to have 2 odd terms and 1 even term, or 3 even terms.
1) If both $(ps)^2$ and $(qr)^2$ are odd then $p,\,s,\,q$ and $r$ are all odd, and so $pqrs$ cannot be even. Thus, this configuration doesn't work.
2) That all terms are even: //to be finished.

 

[Not anonymous]

15. Division of an integer by a prime number $p$ leaves us with the possible remainders $C:=\{\,0,1,2,\ldots ,p-1\,\}\,$. We can define an addition and a multiplication on $C$ if we wrap it around $p$, i.e. we identify $0=p=2p=3p= \ldots \, , 1=1+p=1+2p=1+3p=\ldots ,\ldots$ This is called modular arithmetic (modulo $p$).

Show that for any given numbers $a,b\in C$ the equations $a+x=b$ and $a\cdot x =b$ ($a\neq 0$) have a unique solution.
Is this still true if we drop the requirement that $p$ is prime? (FR)

Remark: This problem is about proof techniques, so be as accurate (not long) as possible, i.e. note which property or condition you use at each step.

Spoiler: Question 15

We first prove for the equation $a+x=b$. We only need to prove that there exists a unique $x$ within the set $C$ that meets the condition $a+x=b$ (modular arithmetic modulo $p$), since if there were any integer $y \notin C$ for which $a + y = b$, then it can be rewritten $a + kp + r = b$, where $k, r$ are quotient and remainder of $y$ when divided by $p$; since $r$ must belong to set $C$ and $a + kp + r = a + r$ by definition of modular arithmetic.

It is obvious that $$x_1 = \begin{cases} (b-a) & \text{if } a \leq b \\
(p-a+b) \text{if } a \gt b \end{cases}$$
is a valid solution for $x$ and that $x_1 \in C$. Suppose this solution is not unique. Then there must be some $x_2 \in C$ such that $x_1 \neq x_2$ and $a+x_2 = b$. Subtracting one expression from the other, we get $(x_2 - x_1) = 0 \mod p$. For simplicity and without loss of generality, we may assume $x_2 \gt x_1$. Since $x_1, x_2 \in C$, even in normal, non-modular arithmetic, $0 \leq (x_2 - x_1) \leq (p-1)$, and therefore $(x_2 - x_1) = 0 \mod p$ implies that $x_2 - x_1 = 0$ in normal arithmetic too and therefore $x_2$ must be equal to $x_1$, a contradiction. Hence $a+x=b$ has a unique solution with $x \in C$.

Proof for existence of $x$ for the multiplication equation $a.x=b$ given $a \neq 0$:
Here too, we only need to prove that there exists a unique $x$ within the set $C$ that meets the condition, since if there were an integer $y \notin C$ such that $a.y = b \mod p$, then, just as before, we can rewrite it as $a(kp + r) = b \Rightarrow (akp + ar) = b \Rightarrow a.r = b$ by definition of modular arithmetic and since $r$ is the remainder of $y$ divided by $p$, $r \in C$.

Consider the modulo $p$ values of the first $p$ non-negative products of $a$, i.e. $0, a, 2a, 3a, ..., (p-1)a$. All these values must be distinct, that is $p$ distinct values from $C$. Otherwise, we would have $x_1 a = x_2 a \mod p$ for some pair of integers $0 \leq x_1 \lt x_2 \leq (p-1)$, implying $(x_2 - x_1) a = 0 \mod p \Rightarrow you = kp$ where $y = (x_2 - x_1)$ and $k$ is some positive integer, but this would imply that $p$ has a prime factor smaller than itself, since $1 \leq a, y \lt p$, which is a contradiction given $p$ is prime. Since the $p$ products have $p$ distinct modulo $p$ values, all elements of $C$ must match exactly one of the $p$ different products. Since $b \in C$, this means that there is exactly one $x \in \{0, 1, 2, \ldots, p-1\} \equiv x \in C$ such that $ax = b \mod p$, it is proven that there exists a unique solution for $a.x = b$ in modular multiplication.

Is this still true if we drop the requirement that p is prime?
If $p$ is not prime, existence of a unique solution is still true for modulo addition, but not for modulo multiplication, since in the proof for uniqueness in solution to multiplication equation, we relied on the fact that $p$ is prime. As an example for non-uniqueness of $a.x = b$ when $p$ is non-prime, consider $a=2, b=6, p=8$. Then we have 2 values of $x \in C$ for which $a.x = b$, namely $x=3$ and $x=7$

 

[Antarres]

Your solution is correct. In order for your solution to be perfect just correct the small typo at the second to last line of your latex.

I'm unable to edit now, but I see what you mean :) was typing too fast I guess.

 

[fresh_42]

.

I'm unable to edit now, but I see what you mean :) was typing too fast I guess.

Done.

 

[Not anonymous]

1. Prove the inequality $cos(θ)^p ≤ cos(pθ)$ for $0≤θ≤π/2$ and $0 < p < 1$. (IR)

The question got an accepted answer before I could post what I had worked out on paper. I don't think my proof would be considered rigorous enough because I make some inferences based on known properties but I am not sure how to put them as formulae, but this is the first non-high school level question from the past several challenges that I found approachable with techniques I studied in school, so I am eager to post what I hope at least comes close to a correct proof.

Spoiler: Question 1

Given $0≤θ≤π/2$ and $0 < p < 1$, the following 2 conditions must be obvious.
1. $0 ≤ cos(θ) ≤ 1 \Rightarrow 0 ≤ cos(θ)^p ≤ 1$
2. $0 ≤ pθ ≤ π/2 \Rightarrow 0 ≤ cos(θ) ≤ 1$

Since both expressions are non-negative, we may apply logarithms to both and use the fact that $\log (x)$ is a monotonically increasing function of $x$ to establish the smaller or larger of 2 values, i.e. $\log (x_1) \geq \log (x_2) \Rightarrow x_1 \geq x_2$

Let $f(x) = \log ({\cos(x)^p}) = p \log (\cos(x))$ and $g(x) = \log (\cos(px))$. Now consider the slopes of these 2 functions.
$$
f'(x) = p \frac {\cos(x)} {-\sin(x)} = -p \tan(x) \\
g'(x) = \frac {\cos(px)} {-\sin(px)} (-p) = -p \tan(px)
$$

When $0 \leq px \leq x \leq π/2$, we have $0 \leq \tan (px) \leq tan(x) \Rightarrow -p \tan(x) \leq -p \tan(px) \leq 0 \Rightarrow f'(x) \leq g'(x) \leq 0$. In other words, $f(x)$ and $g(x)$ are strictly decreasing, continuous functions of $x$ for $x \in [0, π/2]$ and $f(x)$ decreases equally or more rapidly than $g(x)$ for that range of $x$. Since $f(0) = g(0) = \log (\cos(0)) = 0$, this means that $f(θ) \leq g(θ)$ for any given $θ \in [0,π/2]$. By using the earlier stated property of logarithms, this in turn means that the original expressions on which logarithm was applied to get $f(x)$ and $g(x)$ also follow the same inequality, therefore $cos(θ)^p ≤ cos(pθ)$

 

[fresh_42]

.

We first prove for the equation $a+x=b$. We only need to prove that there exists a unique $x$ within the set $C$ that meets the condition $a+x=b$ (modular arithmetic modulo $p$), since if there were any integer $y \notin C$ for which $a + y = b$, then it can be rewritten $a + kp + r = b$, where $k, r$ are quotient and remainder of $y$ when divided by $p$; since $r$ must belong to set $C$ and $a + kp + r = a + r$ by definition of modular arithmetic.

This is true but not necessary. The moment we defined $C$ we were restricted to this set. There are sinply no integers outside, which are under consideration.

It is obvious that $$x_1 = \begin{cases} (b-a) & \text{if } a \leq b \\
(p-a+b) \text{if } a \gt b \end{cases}$$
is a valid solution for $x$ and that $x_1 \in C$.

Correct. Best would have been to show that $-a$ and $0$ exist within $C$, such that $-a+a=0$ and that $C$ is closed under addition, so that $x:=b+(-a) \in C$. The order is problematic, as it only holds for integers, not for elements of $C$. I should have written the elements of $C$ as $[0],[1],\ldots,[p-1]$ to distinguish them. My fault.

Suppose this solution is not unique. Then there must be some $x_2 \in C$ such that $x_1 \neq x_2$ and $a+x_2 = b$. Subtracting one expression from the other, we get $(x_2 - x_1) = 0 \mod p$. For simplicity and without loss of generality, we may assume $x_2 \gt x_1$. Since $x_1, x_2 \in C$, even in normal, non-modular arithmetic, $0 \leq (x_2 - x_1) \leq (p-1)$, and therefore $(x_2 - x_1) = 0 \mod p$ implies that $x_2 - x_1 = 0$ in normal arithmetic too and therefore $x_2$ must be equal to $x_1$, a contradiction. Hence $a+x=b$ has a unique solution with $x \in C$.

Correct. You should in general try to avoid contradictions. In the case above, we can positively conclude $a+x_1=b \,\wedge \, a+x_2=b \Longrightarrow x_1=x_2$.
\begin{align*}
a+x_1=b \,&\wedge \, a+x_2=b \Longrightarrow a+x_1=a+x_2\\
&\Longrightarrow (-a)+(a+x_1)=(-a)+(a+x_2) \quad \text{ existence of additive inverse }\\
&\Longrightarrow (-a+a)+x_1 = (-a+a)+x_2 \quad \text{ associativity of addition inherited from the integers }\\
&\Longrightarrow 0+x_1=0+x_2 \quad \text{ existence of neutral element of addition }\\
&\Longrightarrow x_1 = x_2
\end{align*}
I only mentioned what I had been thought of. Although the elements of $C$ are written as integers, they carry another structure and one has to be careful what is inherited from the integers and what is not.

Proof for existence of $x$ for the multiplication equation $a.x=b$ given $a \neq 0$:
Here too, we only need to prove that there exists a unique $x$ within the set $C$ that meets the condition, since if there were an integer $y \notin C$ such that $a.y = b \mod p$, then, just as before, we can rewrite it as $a(kp + r) = b \Rightarrow (akp + ar) = b \Rightarrow a.r = b$ by definition of modular arithmetic and since $r$ is the remainder of $y$ divided by $p$, $r \in C$.

Consider the modulo $p$ values of the first $p$ non-negative products of $a$, i.e. $0, a, 2a, 3a, ..., (p-1)a$. All these values must be distinct, that is $p$ distinct values from $C$. Otherwise, we would have $x_1 a = x_2 a \mod p$ for some pair of integers $0 \leq x_1 \lt x_2 \leq (p-1)$, implying $(x_2 - x_1) a = 0 \mod p \Rightarrow you = kp$ where $y = (x_2 - x_1)$ and $k$ is some positive integer, but this would imply that $p$ has a prime factor smaller than itself, since $1 \leq a, y \lt p$, which is a contradiction given $p$ is prime. Since the $p$ products have $p$ distinct modulo $p$ values, all elements of $C$ must match exactly one of the $p$ different products. Since $b \in C$, this means that there is exactly one $x \in \{0, 1, 2, \ldots, p-1\} \equiv x \in C$ such that $ax = b \mod p$, it is proven that there exists a unique solution for $a.x = b$ in modular multiplication.

Same as before. We need associativity, a neutral element, inverse elements and closure under multiplication on $C$. With these properties we can solve the equation.

Is this still true if we drop the requirement that p is prime?
If $p$ is not prime, existence of a unique solution is still true for modulo addition, but not for modulo multiplication, since in the proof for uniqueness in solution to multiplication equation, we relied on the fact that $p$ is prime.

The correct definition of a prime number $p$ is: $p \text{ has no multiöpicative inverse and } p|ab \text{ implies } p|a \text{ or }p|b$.

As an example for non-uniqueness of $a.x = b$ when $p$ is non-prime, consider $a=2, b=6, p=8$. Then we have 2 values of $x \in C$ for which $a.x = b$, namely $x=3$ and $x=7$

Yes, primality is necessary in the multiplicative case. From your example we get $2\cdot 3 = 2 \cdot 7 = 6 \mod 8$ which leads to $2\cdot (7-3)=2\cdot 4 = 0$. But if $2\cdot 4= 0$ and $2\cdot 0 = 0$ then we are in trouble. $2$ has no inverse element, since otherwise we would have $4=0$.

 

[Infrared]

@Not anonymous Your argument is good! Just to clarify the part that I assume you're unsure about: Since $f'(x)\leq g'(x),$ the function $h(x)=f(x)-g(x)$ satisfies $h'(x)\leq 0$, so $h$ is decreasing. Since $h(0)=f(0)-g(0)=0-0=0$, this means $h(x)=f(x)-g(x)\leq 0$ on $[0,\pi/2]$, i.e. $f(x)\leq g(x)$.

 

[julian]

I had a go at #10.

Spoiler

We have the identity:

\begin{align}
\left( e^{t {(A+B) \over n}} \right)^n - \left( e^{t {A \over n}} \cdot e^{t {B \over n}} \right)^n & = \left[ e^{t {(A+B) \over n}} - e^{t {A \over n}} \cdot e^{t {B \over n}} \right] \left( e^{t {A \over n}} \cdot e^{t {B \over n}} \right)^{n-1}
\nonumber \\
& + e^{t {(A+B) \over n}} \left[ e^{t {(A+B) \over n}} - e^{t {A \over n}} \cdot e^{t {B \over n}} \right] \left( e^{t {A \over n}} \cdot e^{t {B \over n}} \right)^{n-2}
\nonumber \\
& + \cdots + \left( e^{t {(A+B) \over n}} \right)^{n-1} \left[ e^{t {(A+B) \over n}} - e^{t {A \over n}} \cdot e^{t {B \over n}} \right]
\nonumber
\end{align}

where there are $n$ terms on the RHS. For given $A$, $B$, and fixed $t$ there exists an integer $N$ such that for $n \geq N$

$\left\| {t A \over n} \right\| \leq 1 \; \text{ and } \; \left\| {t B \over n} \right\| \leq 1 .$

Then

\begin{align}
\left\| e^{t (A+B)} - \left( e^{t {A \over n}} \cdot e^{t {A \over n}} \right)^n \right\| & \leq \left\| e^{t {(A+B) \over n}} - e^{t {A \over n}} \cdot e^{t {B \over n}} \right\| \left( \left\| e^{t {A (n-1)\over n}} \right\| \left\| e^{t {B (n-1)\over n}} \right\| \right.
\nonumber \\
& + \left\| e^{t {(A+B) \over n}} \right\| \left\| e^{t {A (n-2)\over n}} \right\| \left\| e^{t {B (n-2)\over n}} \right\|
\nonumber\\
& + \cdots + \left. \left\| e^{t {(A+B) (n-1)\over n}} \right\| \right)
\nonumber\\
& \leq {6 e^2 |t|^2 \over n^2} \left\| [A,B] \right\|
\left( \left\| e^{t {A (n-1)\over n}} \right\| \left\| e^{t {B (n-1)\over n}} \right\| \right.
\nonumber \\
& + \left\| e^{t {(A+B) \over n}} \right\| \left\| e^{t {A (n-2)\over n}} \right\| \left\| e^{t {B (n-2)\over n}} \right\|
\nonumber\\
& + \cdots + \left. \left\| e^{t {(A+B) (n-1)\over n}} \right\| \right)
\nonumber\\
& = {6 e^2 |t|^2 \over n} \left\| [A,B] \right\| \sum_{k=0}^{n-1} \left\| e^{t {A(n-1-k)\over n}} \right\| \left\| e^{t {B (n-1-k)\over n}} \right\| \left\| e^{t {(A+B) k\over n}} \right\| {1 \over n}
\quad *
\nonumber
\end{align}

where we have used the triangle inequality, submultiplicativity, and the estimate in #9.

Is

$g(x) := \left\| e^{t A (1-x)} \right\|$

a continuous function on the closed and bounded interval $[0,1]$? Consider:

\begin{align}
\| e^{t A (1-x_0 \mp \delta)} - e^{t A (1-x_0)} \| & = \| e^{t A (1-x_0)} (e^{\mp t A \delta} - \mathbb{1}) \|
\nonumber\\
& \leq \| e^{t A (1-x_0)} \| \| e^{\mp t A \delta} - \mathbb{1} \|
\nonumber\\
& = \left\| \sum_{k=0}^\infty {t^k A^k (1-x_0)^k \over k!} \right\| \left\| \sum_{l=1}^\infty {t^l (\mp \delta)^l A^l \over l!} \right\|
\nonumber\\
& \leq \sum_{k=0}^\infty {|t|^k \| A^k \| (1-x_0)^k \over k!} \sum_{l=1}^\infty {|t \delta|^l \| A^l \| \over l!}
\nonumber\\
& \leq \sum_{k=0}^\infty {|t|^k \| A \|^k (1-x_0)^k \over k!} \sum_{l=1}^\infty {|t|^l \delta^l \| A \|^l \over l!}
\nonumber\\
& = e^{|t| \| A \| (1-x_0)} ( e^{|t| \| A \| \delta} - 1 ) \quad **
\nonumber
\end{align}

where we have used submultiplicativity, the triangle inequality + homogeneity, and then submultiplicativity again. As we know that $D e^{C x}$, where $D$ and $C$ are constants, is a continuous function we have that for any $\epsilon > 0$ there exists an $\delta$ such that:

$|D e^{C (x_0 \pm \delta)} - D e^{C x_0}| < \epsilon .$

Using this in ** we obtain that for any $\epsilon > 0$ there exists $\delta > 0$ such that

\begin{align}
\| e^{t A (1-x_0 \mp \delta)} - e^{t A (1-x_0)} \| & < \epsilon .
\nonumber
\end{align}

It follows from the triangle inequality that:

$\|M - M' \| \geq \left| \; \|M \| - \| M' \| \; \right| .$

Using this, we obtain that for any $\epsilon > 0$ there exists $\delta > 0$ such that

$\left| \| e^{t A (1-x_0 \mp \delta)} \| - \| e^{t A (1-x_0)}\| \right| \leq \| e^{t A (1-x_0 \mp \delta)} - e^{t A (1-x_0)} \| < \epsilon .$

Hence $g(x)$ is a continuous function on the closed and bounded interval $[0,1]$. By similar considerations, the functions:

$\left\| e^{t B (1-x)} \right\| \text{ and } \left\| e^{t (A+B) x} \right\|$

are also continuous on the closed and bounded interval $[0,1]$. It follows that the function:

$f(x) := \left\| e^{t A (1-x)} \right\| \left\| e^{t B (1-x)} \right\| \left\| e^{t (A+B) x} \right\|$

is continuous on the closed and bounded interval $[0,1]$. It follows (by known results) that it is Riemann-integrable, meaning that the sum in * in the limit where $n \rightarrow \infty$ is equal to $\int_0^1 f(x) dx$.

So that by * we have:

\begin{align}
& \lim_{n \rightarrow \infty} \left\| e^{t (A+B)} - \left( e^{t {A \over n}} \cdot e^{t {B \over n}} \right)^n \right\|
\nonumber\\
&
\leq \lim_{n \rightarrow \infty} {6 e^2 |t|^2 \over n} \| [A,B] \| \times
\int_0^1 dx \left\| e^{t A (1-x)} \right\| \left\| e^{t B (1-x)} \right\| \left\| e^{t (A+B) x} \right\|
\nonumber\\
& = 0
\nonumber
\end{align}

which is the desired result.

 

[fresh_42]

.

I had a go at #10.

Spoiler

We have the identity:

\begin{align}
\left( e^{t {(A+B) \over n}} \right)^n - \left( e^{t {A \over n}} \cdot e^{t {B \over n}} \right)^n & = \left[ e^{t {(A+B) \over n}} - e^{t {A \over n}} \cdot e^{t {B \over n}} \right] \left( e^{t {A \over n}} \cdot e^{t {B \over n}} \right)^{n-1}
\nonumber \\
& + e^{t {(A+B) \over n}} \left[ e^{t {(A+B) \over n}} - e^{t {A \over n}} \cdot e^{t {B \over n}} \right] \left( e^{t {A \over n}} \cdot e^{t {B \over n}} \right)^{n-2}
\nonumber \\
& + \cdots + \left( e^{t {(A+B) \over n}} \right)^{n-1} \left[ e^{t {(A+B) \over n}} - e^{t {A \over n}} \cdot e^{t {B \over n}} \right]
\nonumber
\end{align}

where there are $n$ terms on the RHS. For given $A$, $B$, and fixed $t$ there exists an integer $N$ such that for $n \geq N$

$\left\| {t A \over n} \right\| \leq 1 \; \text{ and } \; \left\| {t B \over n} \right\| \leq 1 .$

Then

\begin{align}
\left\| e^{t (A+B)} - \left( e^{t {A \over n}} \cdot e^{t {A \over n}} \right)^n \right\| & \leq \left\| e^{t {(A+B) \over n}} - e^{t {A \over n}} \cdot e^{t {B \over n}} \right\| \left( \left\| e^{t {A (n-1)\over n}} \right\| \left\| e^{t {B (n-1)\over n}} \right\| \right.
\nonumber \\
& + \left\| e^{t {(A+B) \over n}} \right\| \left\| e^{t {A (n-2)\over n}} \right\| \left\| e^{t {B (n-2)\over n}} \right\|
\nonumber\\
& + \cdots + \left. \left\| e^{t {(A+B) (n-1)\over n}} \right\| \right)
\nonumber\\
& \leq {6 e^2 |t|^2 \over n^2} \left\| [A,B] \right\|
\left( \left\| e^{t {A (n-1)\over n}} \right\| \left\| e^{t {B (n-1)\over n}} \right\| \right.
\nonumber \\
& + \left\| e^{t {(A+B) \over n}} \right\| \left\| e^{t {A (n-2)\over n}} \right\| \left\| e^{t {B (n-2)\over n}} \right\|
\nonumber\\
& + \cdots + \left. \left\| e^{t {(A+B) (n-1)\over n}} \right\| \right)
\nonumber\\
& = {6 e^2 |t|^2 \over n} \left\| [A,B] \right\| \sum_{k=0}^{n-1} \left\| e^{t {A(n-1-k)\over n}} \right\| \left\| e^{t {B (n-1-k)\over n}} \right\| \left\| e^{t {(A+B) k\over n}} \right\| {1 \over n}
\quad *
\nonumber
\end{align}

where we have used the triangle inequality, submultiplicativity, and the estimate in #9.

Is

$g(x) := \left\| e^{t A (1-x)} \right\|$

a continuous function on the closed and bounded interval $[0,1]$? Consider:

\begin{align}
\| e^{t A (1-x_0 \mp \delta)} - e^{t A (1-x_0)} \| & = \| e^{t A (1-x_0)} (e^{\mp t A \delta} - \mathbb{1}) \|
\nonumber\\
& \leq \| e^{t A (1-x_0)} \| \| e^{\mp t A \delta} - \mathbb{1} \|
\nonumber\\
& = \left\| \sum_{k=0}^\infty {t^k A^k (1-x_0)^k \over k!} \right\| \left\| \sum_{l=1}^\infty {t^l (\mp \delta)^l A^l \over l!} \right\|
\nonumber\\
& \leq \sum_{k=0}^\infty {|t|^k \| A^k \| (1-x_0)^k \over k!} \sum_{l=1}^\infty {|t \delta|^l \| A^l \| \over l!}
\nonumber\\
& \leq \sum_{k=0}^\infty {|t|^k \| A \|^k (1-x_0)^k \over k!} \sum_{l=1}^\infty {|t|^l \delta^l \| A \|^l \over l!}
\nonumber\\
& = e^{|t| \| A \| (1-x_0)} ( e^{|t| \| A \| \delta} - 1 ) \quad **
\nonumber
\end{align}

where we have used submultiplicativity, the triangle inequality + homogeneity, and then submultiplicativity again. As we know that $D e^{C x}$, where $D$ and $C$ are constants, is a continuous function we have that for any $\epsilon > 0$ there exists an $\delta$ such that:

$|D e^{C (x_0 \pm \delta)} - D e^{C x_0}| < \epsilon .$

Using this in ** we obtain that for any $\epsilon > 0$ there exists $\delta > 0$ such that

\begin{align}
\| e^{t A (1-x_0 \mp \delta)} - e^{t A (1-x_0)} \| & < \epsilon .
\nonumber
\end{align}

It follows from the triangle inequality that:

$\|M - M' \| \geq \left| \; \|M \| - \| M' \| \; \right| .$

Using this, we obtain that for any $\epsilon > 0$ there exists $\delta > 0$ such that

$\left| \| e^{t A (1-x_0 \mp \delta)} \| - \| e^{t A (1-x_0)}\| \right| \leq \| e^{t A (1-x_0 \mp \delta)} - e^{t A (1-x_0)} \| < \epsilon .$

Hence $g(x)$ is a continuous function on the closed and bounded interval $[0,1]$. By similar considerations, the functions:

$\left\| e^{t B (1-x)} \right\| \text{ and } \left\| e^{t (A+B) x} \right\|$

are also continuous on the closed and bounded interval $[0,1]$. It follows that the function:

$f(x) := \left\| e^{t A (1-x)} \right\| \left\| e^{t B (1-x)} \right\| \left\| e^{t (A+B) x} \right\|$

is continuous on the closed and bounded interval $[0,1]$. It follows (by known results) that it is Riemann-integrable, meaning that the sum in * in the limit where $n \rightarrow \infty$ is equal to $\int_0^1 f(x) dx$.

So that by * we have:

\begin{align}
& \lim_{n \rightarrow \infty} \left\| e^{t (A+B)} - \left( e^{t {A \over n}} \cdot e^{t {B \over n}} \right)^n \right\|
\nonumber\\
&
\leq \lim_{n \rightarrow \infty} {6 e^2 |t|^2 \over n} \| [A,B] \| \times
\int_0^1 dx \left\| e^{t A (1-x)} \right\| \left\| e^{t B (1-x)} \right\| \left\| e^{t (A+B) x} \right\|
\nonumber\\
& = 0
\nonumber
\end{align}

which is the desired result.

Well done. I think from (*) on it can be shortened by an estimation with $e^{\|tA\|},e^{\|tB\|}$, and in general by putting $t$ into the matrices until the very end.

 

[suremarc]

2. Let $F:\mathbb{R}^n\to\mathbb{R}^n$ be a continuous function such that $||F(x)-F(y)||\geq ||x-y||$ for all $x,y\in\mathbb{R}^n$. Show that $F$ is a homeomorphism. (IR)

Spoiler: Solution

A function between topological spaces is a homeomorphism iff it is a continuous bijection with a continuous inverse. Given that $F$ is continuous, we prove that F is injective, thus there exists a left inverse $G$; we then prove that $G$ is continuous, and then finally we prove that the image of $F$ is all of $\mathbb{R}^n$. First, note that if $F(x)=F(y)$, then $0=\|F(x)-F(y)\|\geq\|x-y\|\Rightarrow x=y$. Thus, $F$ is injective and has a left inverse $G:\mathrm{im}(F)\rightarrow\mathbb{R}^n$.

Now we prove that $G$ is continuous (in fact, it is uniformly continuous). The $\varepsilon,\delta$-definition of uniform continuity in a metric space is the following: $$(\forall\varepsilon>0)(\exists\delta>0)(\forall x,y\in\mathrm{im}(F))\quad\|x-y\|<\delta\Rightarrow\|G(x)-G(y)\|<\varepsilon.$$ Given $\varepsilon$, we choose $\delta(\varepsilon)=\varepsilon$. Since $x,y\in\mathrm{im}(F)$, there exist $x',y'\in\mathbb{R}^n$ with $F(x')=x,\ F(y')=y$. Then $\|G(x)-G(y)\|=\|x'-y'\|$ since $G$ is a left inverse of $F$. By the inequality specified in the problem statement, we have $\|G(x)-G(y)\|=\|x'-y'\|\leq\|F(x')-F(y')\|=\|x-y\|$. By transitivity, $\|x-y\|<\delta(\varepsilon)=\varepsilon\Rightarrow\|G(x)-G(y)\|<\varepsilon$. We have proved that $G$ is continuous.

We have proven that $F$ is a homeomorphism onto its image. We now prove that the image of $F$ is all of $\mathbb{R}^n$ as follows: prove that $\mathrm{im}(F)$ is both open and closed in $\mathbb{R}^n$, and since the only clopen sets in a connected space are the empty set and the whole space, the image of $F$ must be all of $\mathbb{R}^n$.

Openness of $\mathrm{im}(F)$ follows from continuity of $G$, so we need only show that the image is closed. In a complete metric space, this is equivalent to proving that the limit of a Cauchy sequence in the image is also contained in the image. Suppose $c_n\rightarrow c$ with $c_n\in\mathrm{im}(F)$. Thus there exists a sequence $x_n\in\mathbb{R}^n$ with $F(x_n)=c_n$. The definition of a Cauchy sequence states that $$(\forall\varepsilon>0)(\exists N\in\mathbb{N})(\forall m,n>\mathbb{N})\quad\|c_m-c_n\|<\varepsilon\\\Rightarrow\|x_m-x_n\|\leq\|F(x_m)-F(x_n)\|=\|c_m-c_n\|<\varepsilon$$ by the inequality in the problem statement. Thus, $x_n$ is also Cauchy with limit $x_n\rightarrow x\in\mathbb{R}^n$. Then one has $\|F(x)-c_n\|\rightarrow 0$. Since the limit of a sequence is unique, it must be true that $c=F(x)$, proving that $c\in\mathrm{im}(F)$.

We have shown that the image of $F$ is clopen. Since a nonempty clopen set in a connected space is the whole space, the image of $F$ is all of $\mathbb{R}^n$. Altogether, we have shown that $F$ a continuous bijection with a continuous inverse, proving that $F$ is a homeomorphism. $\square$

9. Let $A,B\in \mathbb{M}(m,\mathbb{R})$ and $\|A\|,\|B\|\leq 1$ with a submultiplicative matrix norm, then $$\left\|\,e^{A+B}-e^A\cdot e^B\,\right\|\leq 6e^2\cdot \left\|\,[A,B]\,\right\|$$(FR)

This problem took me 3 days, so hopefully I didn't mess up

I expect that there is almost certainly a much easier way to do this problem, which I could not find. But I did manage to obtain a much better bound, so I suppose there's that.

Spoiler: Solution

We use the following result from https://www.researchgate.net/publication/318418316_The_Non-Commutative_Binomial_Theorem: in any unital Banach algebra, we have $$e^{X+Y}=e^Xe^Y+\left(\sum_{n=0}^\infty\frac{D_n(Y,X)}{n!}\right)e^Y$$ where $$D_{n+1}(Y,X)=[Y,X^n+D_n(Y,X)]+X\cdot D_n(Y,X)$$ is defined by a recurrence relation, with $D_0(Y,X)=D_1(Y,X)=0$. From this it is clear that $D_2(Y,X)=[Y,X]$.

Assume that $X,Y\in\mathcal{A}$ where $\mathcal{A}$ is a unital Banach algebra. Our strategy is as follows: factor the non-commuting part as $\gamma([Y,X])$, where $\gamma$ is some element of the operator algebra $B(\mathcal{A})$ dependent on $X$ and $Y$, then obtain bounds on its operator norm. Firstly, let us work in the enveloping algebra of $\mathcal{A}$. Let us denote $\mathrm{ad}_X=L_X-R_X$. We can rewrite $D_n$ in the following manner: $$D_{n+1}(Y,X)=[Y,X^n]+(L_X+\mathrm{ad}_Y)(D_n(Y,X)).$$ Our goal is to rewrite $D_n$ as a linear combination of previous elements in the sequence, for reasons that will become clear. Observe that $[Y,X^n]=[Y,X^{n-1}]X+X^{n-1}[Y,X]$. Since $D_{n+1}-(L_X+\mathrm{ad}_Y)D_n=[Y,X^n]$, we have $$[Y,X^n]=[Y,X^{n-1}]X+X^{n-1}[Y,X]=\left(D_n-(L_X+\mathrm{ad}_Y)(D_{n-1})\right)X+X^{n-1}[Y,X].$$ This implies that we can rewrite $D_n$ in the following manner: $$D_{n+2}=(D_{n+1}-(L_X+\mathrm{ad}_Y)(D_{n}))X+X^n[Y,X]+(L_X+\mathrm{ad}_Y)(D_{n+1})\\=X^n[Y,X]+(L_X+R_X+\mathrm{ad}_Y)(D_{n+1})-R_X(L_X+\mathrm{ad}_Y)(D_n).$$ Now, suppose that there exists $\Gamma_n\in B(\mathcal{A})$ for $n<k$ such that $\Gamma_n([Y,X])=D_n(Y,X)$. Then, provided that $k\geq 2$, one can find $\Gamma_k$ such that $\Gamma_k([Y,X])=D_k(Y,X)$, using the second-order equation for $D_n$: $$\Gamma_k=L_{X^{k-2}}+(L_X+R_X+\mathrm{ad}_Y)\Gamma_{k-1}-R_X(L_X+\mathrm{ad}_Y)\Gamma_k.$$ Letting $\Gamma_0=\Gamma_1=0$, we have $k=2$ and the formula holds for all $\Gamma_n$ by induction. (In particular, $\Gamma_2=\mathrm{id_{\mathcal{A}}}$.) Now let $\gamma=\sum_{n=0}^\infty\frac{\Gamma_n}{n!}$ and we have the formula $e^{X+Y}-e^Xe^Y = \gamma([Y,X])\cdot e^Y$.

Now we obtain bounds on the operator norm of $\gamma$, for $\|e^{X+Y}-e^Xe^Y\|\leq\|\gamma\|_{\mathrm{op}}\,\|[Y,X]\|\,\|e^Y\|$. First note that
$$\|\gamma\|_{\mathrm{op}}\leq\sum_{n=0}^\infty\frac{\|\Gamma_n\|_{\mathrm{op}}}{n!}$$ by subadditivity. From the defining recurrence relation of $\Gamma_n$, we have the following inequality: $$\|\Gamma_{n+2}\|\leq\|L_X\|^n+(\|L_X\|+\|R_X\|+\|\mathrm{ad}_Y\|\,\|\Gamma_{n+1}\|+\|R_X\|(\|L_X\|+\|\mathrm{ad}_Y\|)\,\|\Gamma_n\|$$ by subadditivity and submultiplicativity of the operator norm. We can make substitutions based on the fact that $\|L_X\|_{\mathrm{op}},\|R_X\|_{\mathrm{op}}\leq\|X\|_{\mathcal{A}}$, implying that $\|\mathrm{ad}_Y\|_{\mathrm{op}}\leq 2\|Y\|_{\mathcal{A}}$. Suppose $\|X\|,\|Y\|\leq C$. Then we have the inequality $$\|\Gamma_{n+2}\|\leq C^n+4C\|\Gamma_{n+1}\|+3C^2\|\Gamma_n\|.$$ Roughly, this suggests that $\|\Gamma_n\|=O(C^{n-2})$ when n is held constant, which we will now make more precise. Let $$a_{n+2}=1+4a_{n+1}+3a_n;\quad a_0=a_1=0.$$ If we have $a_n\geq\|\Gamma_n\|C^{n-2}$ for $n<k$, then one has $$\|\Gamma_k\|\leq C^{k-2}+4C\|\Gamma_{k-1}\|+3C^2\|\Gamma_{k-2}\|\\\leq C^k+4C\cdot C^{k-3}a_{k-1}+3C^2\cdot C^{k-4}a_{k-2}\\=C^{k-2}(1+4a_{k-1}+3a_{k-2})=C^{k-2}a_k$$ which is valid, provided that $k\geq 4$. Observing that the inequality holds for $\|\Gamma_2\|=1$ and $\|\Gamma_3\|\leq 5C$, the inequality holds for all $n\in\mathbb{N}$ by induction.

We now return to the operator $\gamma$: applying the inequality for $\|\gamma\|$ in terms of $\Gamma_n$, we have that $$\|\gamma\|\leq\sum_{n=2}^\infty\frac{C^{n-2}a_n}{n!}$$ The right-hand side is equivalent to $f(C)/C^2$, where $f$ is the unique solution to the differential equation $f''(t)=e^t+4f'(t)+3f(t)$ with $f(0)=0, f'(0)=0$. It can be written as $$f(t)=\frac{1}{84}\left((7-\sqrt{7})e^{(2+\sqrt{7})t}+(7+\sqrt{7})e^{(2-\sqrt{7})t}-14e^t\right).$$ We now have the bound $$\|e^{X+Y}-e^Xe^Y\|\leq\frac{f(C)}{C^2}\|[Y,X]\|\,\|e^Y\|\\\leq\frac{f(C)}{C^2}\|[Y,X]\|e^{\|Y\|}\\\leq\frac{f(C)}{C^2}e^C\|[Y,X]\|.$$ In the case that $\|X\|,\|Y\|\leq 1$, one let's $C\rightarrow 1$: $$\|e^{X+Y}-e^Xe^Y\|\leq f(1)e\|[Y,X]\|\approx 5.01e\|[Y,X]\|\leq 6e^2\|[Y,X]\|.$$ Thus, we have improved significantly on the original inequality.

 

[fresh_42]

This problem took me 3 days, so hopefully I didn't mess up

I expect that there is almost certainly a much easier way to do this problem, which I could not find. But I did manage to obtain a much better bound, so I suppose there's that.

Spoiler: Solution

We use the following result from https://www.researchgate.net/publication/318418316_The_Non-Commutative_Binomial_Theorem: in any unital Banach algebra, we have $$e^{X+Y}=e^Xe^Y+\left(\sum_{n=0}^\infty\frac{D_n(Y,X)}{n!}\right)e^Y$$ where $$D_{n+1}(Y,X)=[Y,X^n+D_n(Y,X)]+X\cdot D_n(Y,X)$$ is defined by a recurrence relation, with $D_0(Y,X)=D_1(Y,X)=0$. From this it is clear that $D_2(Y,X)=[Y,X]$.

Assume that $X,Y\in\mathcal{A}$ where $\mathcal{A}$ is a unital Banach algebra. Our strategy is as follows: factor the non-commuting part as $\gamma([Y,X])$, where $\gamma$ is some element of the operator algebra $B(\mathcal{A})$ dependent on $X$ and $Y$, then obtain bounds on its operator norm. Firstly, let us work in the enveloping algebra of $\mathcal{A}$. Let us denote $\mathrm{ad}_X=L_X-R_X$. We can rewrite $D_n$ in the following manner: $$D_{n+1}(Y,X)=[Y,X^n]+(L_X+\mathrm{ad}_Y)(D_n(Y,X)).$$ Our goal is to rewrite $D_n$ as a linear combination of previous elements in the sequence, for reasons that will become clear. Observe that $[Y,X^n]=[Y,X^{n-1}]X+X^{n-1}[Y,X]$. Since $D_{n+1}-(L_X+\mathrm{ad}_Y)D_n=[Y,X^n]$, we have $$[Y,X^n]=[Y,X^{n-1}]X+X^{n-1}[Y,X]=\left(D_n-(L_X+\mathrm{ad}_Y)(D_{n-1})\right)X+X^{n-1}[Y,X].$$ This implies that we can rewrite $D_n$ in the following manner: $$D_{n+2}=(D_{n+1}-(L_X+\mathrm{ad}_Y)(D_{n}))X+X^n[Y,X]+(L_X+\mathrm{ad}_Y)(D_{n+1})\\=X^n[Y,X]+(L_X+R_X+\mathrm{ad}_Y)(D_{n+1})-R_X(L_X+\mathrm{ad}_Y)(D_n).$$ Now, suppose that there exists $\Gamma_n\in B(\mathcal{A})$ for $n<k$ such that $\Gamma_n([Y,X])=D_n(Y,X)$. Then, provided that $k\geq 2$, one can find $\Gamma_k$ such that $\Gamma_k([Y,X])=D_k(Y,X)$, using the second-order equation for $D_n$: $$\Gamma_k=L_{X^{k-2}}+(L_X+R_X+\mathrm{ad}_Y)\Gamma_{k-1}-R_X(L_X+\mathrm{ad}_Y)\Gamma_k.$$ Letting $\Gamma_0=\Gamma_1=0$, we have $k=2$ and the formula holds for all $\Gamma_n$ by induction. (In particular, $\Gamma_2=\mathrm{id_{\mathcal{A}}}$.) Now let $\gamma=\sum_{n=0}^\infty\frac{\Gamma_n}{n!}$ and we have the formula $e^{X+Y}-e^Xe^Y = \gamma([Y,X])\cdot e^Y$.

Now we obtain bounds on the operator norm of $\gamma$, for $\|e^{X+Y}-e^Xe^Y\|\leq\|\gamma\|_{\mathrm{op}}\,\|[Y,X]\|\,\|e^Y\|$. First note that
$$\|\gamma\|_{\mathrm{op}}\leq\sum_{n=0}^\infty\frac{\|\Gamma_n\|_{\mathrm{op}}}{n!}$$ by subadditivity. From the defining recurrence relation of $\Gamma_n$, we have the following inequality: $$\|\Gamma_{n+2}\|\leq\|L_X\|^n+(\|L_X\|+\|R_X\|+\|\mathrm{ad}_Y\|\,\|\Gamma_{n+1}\|+\|R_X\|(\|L_X\|+\|\mathrm{ad}_Y\|)\,\|\Gamma_n\|$$ by subadditivity and submultiplicativity of the operator norm. We can make substitutions based on the fact that $\|L_X\|_{\mathrm{op}},\|R_X\|_{\mathrm{op}}\leq\|X\|_{\mathcal{A}}$, implying that $\|\mathrm{ad}_Y\|_{\mathrm{op}}\leq 2\|Y\|_{\mathcal{A}}$. Suppose $\|X\|,\|Y\|\leq C$. Then we have the inequality $$\|\Gamma_{n+2}\|\leq C^n+4C\|\Gamma_{n+1}\|+3C^2\|\Gamma_n\|.$$ Roughly, this suggests that $\|\Gamma_n\|=O(C^{n-2})$ when n is held constant, which we will now make more precise. Let $$a_{n+2}=1+4a_{n+1}+3a_n;\quad a_0=a_1=0.$$ If we have $a_n\geq\|\Gamma_n\|C^{n-2}$ for $n<k$, then one has $$\|\Gamma_k\|\leq C^{k-2}+4C\|\Gamma_{k-1}\|+3C^2\|\Gamma_{k-2}\|\\\leq C^k+4C\cdot C^{k-3}a_{k-1}+3C^2\cdot C^{k-4}a_{k-2}\\=C^{k-2}(1+4a_{k-1}+3a_{k-2})=C^{k-2}a_k$$ which is valid, provided that $k\geq 4$. Observing that the inequality holds for $\|\Gamma_2\|=1$ and $\|\Gamma_3\|\leq 5C$, the inequality holds for all $n\in\mathbb{N}$ by induction.

We now return to the operator $\gamma$: applying the inequality for $\|\gamma\|$ in terms of $\Gamma_n$, we have that $$\|\gamma\|\leq\sum_{n=2}^\infty\frac{C^{n-2}a_n}{n!}$$ The right-hand side is equivalent to $f(C)/C^2$, where $f$ is the unique solution to the differential equation $f''(t)=e^t+4f'(t)+3f(t)$ with $f(0)=0, f'(0)=0$. It can be written as $$f(t)=\frac{1}{84}\left((7-\sqrt{7})e^{(2+\sqrt{7})t}+(7+\sqrt{7})e^{(2-\sqrt{7})t}-14e^t\right).$$ We now have the bound $$\|e^{X+Y}-e^Xe^Y\|\leq\frac{f(C)}{C^2}\|[Y,X]\|\,\|e^Y\|\\\leq\frac{f(C)}{C^2}\|[Y,X]\|e^{\|Y\|}\\\leq\frac{f(C)}{C^2}e^C\|[Y,X]\|.$$ In the case that $\|X\|,\|Y\|\leq 1$, one let's $C\rightarrow 1$: $$\|e^{X+Y}-e^Xe^Y\|\leq f(1)e\|[Y,X]\|\approx 5.01e\|[Y,X]\|\leq 6e^2\|[Y,X]\|.$$ Thus, we have improved significantly on the original inequality.

This will take me some time to check, although I'm pretty sure it is right. You have used some big canons in there! My solutions only uses Bubble Sort

The result is used to prove H.F. Trotter's formula (problem 10) where the factor is irrelevant. I liked these two formulas, because they are probably useful for physicists.

 

[Not anonymous]

13. Let $\mathbb{Q}\to\mathbb{Q}$ be the function $f(x)=x^3-2x$. Show that $f$ is injective. (IR)

I think there should be a solution simpler than whatever I could get so far, but I guess such a solution would use some property or identity that I am unfamiliar with.

Spoiler: Question 13

To prove that the function is injective in the domain of $\mathbb{Q}$, we need to show that there cannot be 2 different rational numbers that are mapped to the same value by function $f$. Suppose $f$ is not injective in the domain of rational numbers, then there must be at least 2 different rational numbers, say $x, y$ such that $f(x) = f(y)$. Without loss of generality, we may write $y$ as $y=x+z$ where $z > 0$ and $z \in \mathbb{Q}$ (I assume that it is obvious that $\mathbb{Q}$ is closed under addition).

Therefore,
$$
f(x) = f(x+z) \Rightarrow f(x+z) - f(x) = 0 \Rightarrow (x+z)^3 - 2(x+z) - x^3 + 2x = 0 \\
\Rightarrow z(x^2 + (x+z)^2 +x(x+z)) - 2z = 0 \Rightarrow (3x^2 + 3zx + z^2 - 2) = 0 \Rightarrow (3x^2 + 3zx + z^2 - 2) = 0
$$
with the last step equation arising because $z$ cannot be 0 be definition.

We solve the above quadratic equation considering $x$ as the variable and obtain solutions in terms of $z$.
$x = \dfrac {-3z \pm \sqrt{9z^2 - 12z^2 + 24}} {6z} = \dfrac {-3z \pm \sqrt{24 - 3z^2}} {6z}$

Since rational numbers are closed under addition, multiplication and division (except division by zero), if we want $x$ to be rational as per original assumption, we need all terms in the RHS of above equation to be rational and therefore $\sqrt{24 - 3z^2}$ must be a rational number. Since $z$ is positive rational number, it can be written as $a/b$ where $a,b$ are coprime positive integers. Therefore,

$\sqrt{24 - 3z^2} \in \mathbb{Q} \Rightarrow \dfrac {\sqrt{24b^2 - 3a^2}} {b} \in \mathbb{Q} \Rightarrow {\sqrt{24b^2 - 3a^2}} \in \mathbb{Q}$

Since ${24b^2 - 3a^2}$ is also an integer, the condition ${\sqrt{24b^2 - 3a^2}} \in \mathbb{Q}$ requires $(24b^2 - 3a^2)$ to be a perfect square (since square root of a whole number is a rational number only if it is a perfect square). Since $(24b^2 - 3a^2) = 3(8b^2 - a^2)$, it being a perfect square requires that $(8b^2 - a^2)$ must have an odd number as exponent of 3 in its prime factorization (since otherwise the product $3(8b^2 - a^2)$ will have an odd exponent of 3 and so cannot be a perfect square). Thus, $(8b^2 - a^2) \mod 3 = 0$.

We now consider various possible combinations of modulo 3 values for $a$ and $b$ and show that none of them lead to $(8b^2 - a^2) \mod 3 = 0$. We do not consider the modulo 3 combination $(0, 0)$ since that would mean both $a,b$ are multiples of 3, violating the assumption that they are coprime.

$a \mod 3$	$b \mod 3$	$(8b^2 - a^2) \mod 3$
0	1	2
0	2	2
1	0	2
1	1	1
1	2	1
2	0	2
2	1	1
2	2	1

Thus, there exists no pair of corpime positive integers, $(a,b)$, which satisfies the criterion $(8b^2 - a^2) \mod 3 = 0$. This implies that we cannot find a coprime integer pair $(a,b)$ for which $24b^2 - 3a^2$ will be a perfect square. Hence, as per the quadratic equation for $x$, there is no rational-valued solution for $x$ is $z \in \mathbb{Q}$, i.e. not both $x$ and $z$ can be rational, i.e. the requirement for function $f$ to be non-injective cannot be met. Hence $f$ must be an injective function.

 

[Infrared]

@suremarc Your solution is good, but you could elaborate on why $F(\mathbb{R}^n)$ is open?

Openness of $\mathrm{im}(F)$ follows from continuity of $G$

Keep in mind that a function that is a homeomorphism onto its image does not always have open image (e.g. embed $\mathbb{R}\hookrightarrow\mathbb{R}^2$ in the obvious way).@Not anonymous Nice work! There is a also solution using parity arguments along the lines of post 14, but this argument is good too.

 

[Adesh]

High School :-
Question 13. Let $f : \mathbb Q \rightarrow \mathbb Q$ be the function $f(x) = x^3 -2x$. Show that $f$ is injective.

https://drive.google.com/file/d/1uLMRllrzimUW65IzqwOL9JIdOuG3RfTz/view?usp=sharing

 

[Infrared]

@Adesh You argue that for $x_2$ to be rational, that $\sqrt{8-3x_1^2}$ must be rational, so $8-3x_1^2$ must be a perfect square. However, this only means that $8-3x_1^2$ is the square of a rational, not necessarily of an integer, so you can't conclude that it has to be $4$ or $1$.

@Not anonymous gave a proof with the same idea (quadratic formula) in post 47 you could look at.