Math Challenge - April 2020

[fresh_42]

Questions

1. (solved by @nuuskur ) Let $U\subseteq X$ be a dense subset of a normed vector space, $Y$ a Banach space and $A\in L(U,Y)$ a linear, bounded operator. Show that there is a unique continuation $\tilde{A}\in L(X,Y)$ with $\left.\tilde{A}\right|_U = A$ and $\|\tilde{A}\|=\|A\|\,.$ (FR)

2. Let $X\sim \mathcal{N}(\mu, \sigma^2)$ and $Y\sim \mathcal{N}(\lambda,\sigma^2)$ be normally distributed random variables on $\mathbb{R}$ with expectation values $\mu,\lambda \in \mathbb{R}$ and standard deviation $\sigma$. We want to test the hypothesis that $\mu =\lambda$ with $n$ independent measurements $X_1,\ldots,X_n$ and $Y_1,\ldots, Y_n\,.$ We choose the mean distance
$$
T_n(X_1,Y_1;X_2,Y_2;\ldots;X_n,Y_n) :=\dfrac{1}{n}\sum_{k=1}^n\left(X_k-Y_k\right)
$$
as estimator for the difference $\nu=\mu-\lambda\,.$
a) Does the estimator $T_n$ have a bias and is it consistent?
b) Let $n=100$ and $\sigma^2=0.5\,.$ We use the hypotheses $H_0\, : \,\mu=\lambda$ and $H_1\, : \,\mu\neq\lambda\,.$ Determine a reasonable deterministic test $\varphi$ for the error level $\alpha=0.05\,.$ (FR)

3. (solved by @Antarres )
a) Solve $y'' x^2-12y=0,\,y(0)=0,\,y(1)=16$ and calculate
$$
\sum_{n=1}^\infty \dfrac{1}{t_n},\;t_n:=y(n)-\dfrac{1}{2}y'(n)+\dfrac{1}{8}y''(n)-\dfrac{1}{48}y'''(n)+\dfrac{1}{384}y^{(4)}(n).
$$
b) What do we get for the initial values $y(1)=1,\,y(-1)=-1$ and $\displaystyle{\sum_{n=1}^\infty \left(y'(n)+y'''(n)\right)}?$ (FR)

4. (solved by @Fred Wright ) Solve the initial value problem $y'(x)=y(x)^2-(2x+1)y(x)+1+x+x^2$ for $y(0)\in \{\,0,1,2\,\}\,.$ (FR)

5. (solved by @Lament ) For coprime natural numbers $n,m$ show that
$$
m^{\varphi(n)}+n^{\varphi(m)} \equiv 1 \operatorname{mod} nm
$$
(FR)

6. (solved by @Not anonymous ) If $a_1,a_2 > 0$ and $m_1,m_2 \geq 0$ with $m_1 + m_2 = 1$ show that $a_1^{m_1}a_2^{m_2} < m_1 a_1 + m_2 a_2.$ (QQ)

7. (solved by @Adesh ) Let $f$ be a three times differentiable function with $f^{'''}$ continuous at $x = a$ and $f^{'''}(a) \neq 0$. Now, let's take the expression $f(a + h) = f(a) + hf'(a) + \frac{h^2}{2!}f''(a + \theta h)$ with $0 < \theta < 1$ which holds true for $f$. Show that $\theta$ tends to $\frac{1}{3}$ as $h \rightarrow 0.$ (QQ)

8. (solved by @archaic ) How many real zeros does the polynomial $p_n(x) = 1+x+x^2/2 + \ldots + x^n/n!$ have? (IR)

9. (solved by @Lament , @Adesh ) Let $f:[0,1]\to [0,1]$ be a continuous function such that $f(f(f(x)))=x$ for all $x\in [0,1]$. Show that $f$ must be the identity function $f(x)=x.$ (IR)

10. (solved by @Not anonymous , @wrobel ) Let $f:[0,1]\to\mathbb{R}$ be a continuous function, differentiable on $(0,1)$ that satisfies $f(0)=f(1)=0.$ Prove that $f(x)=f'(x)$ for some $x\in (0,1)$. Note that $f'$ is not assumed to be continuous. (IR)

High Schoolers only

11. (solved by @archaic ) Let $P(x)=x^n+a_{n-1}x^{n-1}+\ldots +a_1x+a_0$ a monic, real polynomial of degree $n$, whose zeros are all negative.
Show that $\displaystyle{\int_1^\infty}\dfrac{dx}{P(x)}$ converges absolutely if and only if $n\geq 2.$ (FR)

12. A table has an internal movable surface used for slicing bread. In order to be able to be pulled to the outside, there are two small handles on its front face with distance $a$ between them put in a symmetric way with respect to the middle of the surface. The length of the surface is $L$ ($Fig.1$). Find the minimum friction coefficient $K$ between the sides of the movable surface and the internal surface of the respective sides of the table, so that we can pull the movable surface using only the one handle whatever force magnitude (i.e. big force) we exert. (QQ)

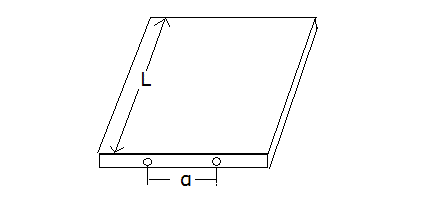
$Fig.1$

13. a.) (solved by @Adesh ) Using only trigonometric substitutions find if $\lim_{x\to\frac{\pi}{2}} \frac{x - \frac{\pi}{2}}{\sqrt{1 - \sin x}}$ exists.
b.) (solved by @archaic ) Find $\lim_{x\to\infty} [\ln(e^x + e^{-x}) - x]$ (QQ)

14. (solved by @Not anonymous ) Let $p$ be a prime number all of whose digits are $1$. Show that $p$ must have a prime number of digits. (IR)

15. (solved by @Not anonymous ) How many ways can you tile a $2\times n$ rectangle with $1\times 2$ and $2\times 1$ rectangles? (IR)

 

[Antarres]

Spoiler: Question #3

a)
We assume the solution of form: $y(x) = x^s$ for some real number $s$. Substituting we find:
$$s(s-1) - 12 = 0$$
after dividing by $x^s$. This equation has two solutions: $s_1 = 4$ and $s_2 = -3$, so we find the general solution of he equation:
$$y = Ax^4 + \frac{B}{x^3}$$
We now substitute initial conditions. $y(0)=0$ must give $B=0$ otherwise the function would be undefined at zero. $y(1) = 16$ gives $A=16$. We finally find the solution $y = 16x^4$.

Now we calculate:
$$t_n = 16n^4 - 32n^3 + 24n^2 - 8n + 1 = (2n-1)^4$$
So finally, we find that the series we need to sum is:
$$\sum_{n=1}^\infty \frac{1}{(2n-1)^4}$$
If we take that we know the known sum of the series(if this can't be assumed, I can post a proof later):
$$\sum_{n=1}^\infty \frac{1}{n^4} = \zeta(4) = \frac{\pi^4}{90}$$
then:
$$\sum_{n=1}^\infty \frac{1}{n^4} = \sum_{n=1}^\infty \left(\frac{1}{(2n-1)^4}+\frac{1}{(2n)^4}\right) = \sum_{n=1}^\infty \frac{(2n-1)^4} + \sum_{n=1}^\infty \frac{1}{16n^4}$$
From this we have:
$$\sum_{n=1}^\infty \frac{1}{(2n-1)^4} = \frac{15\pi^4}{1440}$$

b) If we take different initial conditions $y(1) = -1$, $y(-1)=1$, then we have:
$$A + B = -1 \qquad A-B = 1$$
from which we have: $y = -\frac{1}{x^3}$($A=0 \quad B=-1$).
Then the sum turns into the following:
$$\sum_{n=1}^\infty \frac{3}{n^4} + \frac{60}{n^6} = \frac{3\pi^4}{90} + \frac{60\pi^6}{945} = \frac{\pi^4}{30} + \frac{4\pi^6}{63}$$
Where again I've used the known zeta function value $\zeta(6) = \frac{\pi^6}{945}$. There is a way to sum those series, for example, they usually occurred as part of some Fourier series exercise during studies, or we can use the formula for zeta function values for even numbers(in terms of Bernoulli numbers), which is what I referenced to. If the point of the exercise was to find this way of summing as well, I will post it in the next post.

 

[fresh_42]

If the point of the exercise was to find this way of summing as well, I will post it in the next post.

Please try to write complete solutions, i.e. in one post. Otherwise I cannot only not link it, it is also almost impossible to read for others. So in case you actually calculate the sum, please provide a post with a full solution.

Your solutions are correct, up to:

$\dfrac{15\pi^4}{1440}=\dfrac{\pi^4}{96}$, a missing sign in the answer to b), and the fact that I have no idea what you meant in the calculation for a) with the plus sign alone in the denominator. You may use values of the zeta function, but you should have explained why you used which value where.

It's basically impossible to see how you found the answer. You left out too many steps in my opinion.

This is what I meant:
a.)
\begin{align*}
\sum_{n=1}^\infty \dfrac{1}{t_n}&= \sum_{n=1}^\infty \dfrac{1}{(2n-1)^4}
=\dfrac{1}{2}\left(\sum_{n=1}^\infty\dfrac{1}{n^4} + \sum_{n=1}^\infty\dfrac{(-1)^{n-1}}{n^4} \right)\\
&=\dfrac{1}{2}\left(\zeta(4)+(1-2^{1-4})\cdot\zeta(4)\right)=\dfrac{15}{16}\cdot \dfrac{\pi^4}{90}=\dfrac{\pi^4}{96} \approx 1.014678
\end{align*}

b.)
\begin{align*}
\sum_{n=1}^\infty \left(y'(n)+y'''(n)\right)&=\sum_{n=1}^\infty \left(-3x^{-4}-60x^{-6}\right)\\&=-3\cdot\zeta(4)-60\cdot\zeta(6)\\&= -\dfrac{3\pi^4}{90}-\dfrac{60\pi^6}{945}\\&=-\dfrac{\pi^4}{30}-\dfrac{4\pi^6}{63}\approx -64.2875534202
\end{align*}

 

[Not anonymous]

14. Let $p$ be a prime number all of whose digits are $1$. Show that $p$ must have a prime number of digits. (IR)

Spoiler: Question 14

We use the following identity in the proof:
Identity 1: For any positive integer $n$ and real number $x$, $$x^n - 1 = x^n - 1^n = (x-1)(x^{n-1} + x^{n-2} + \ldots + 1)$$

Proof:
Let $N$ be the number of digits in the decimal representation of $p$. Since all digits are $1$, $$
p = \sum_{i=0}^{N-1} 10^i = \dfrac {10^{N} - 1} {10 - 1} = \dfrac {10^{N} - 1} {9} \\
\Rightarrow 9p = 10^{N} - 1
$$

Suppose $N$ is not prime. Then $N$ can be written as the product of two positive integers greater than 1, i.e. $N = ab , \text{where } a,b \geq 2$. Substituting for $N$ in the earlier equality gives $$
9p = 10^{ab} - 1 = (10^{a})^{b} - 1 = (10^{a} - 1)(10^{a(b-1)} + 10^{a(b-2)} + \ldots + 10^{0}) = \\
\Rightarrow 9p = (10^{a} - 1) \times S \text{ where } S = \sum_{j=0}^{b-1} 10^{ja}
$$

Since $a, b \geq 2$, $S \geq 101$

It is easy to show that $9 ∣ (10^{a} - 1)$ for any positive integer $a$ and that for $a \geq 1$, $(10^{a} - 1) = 9q$ where integer $q \gt 1$. It follows that $9p = 9qS \Rightarrow p = qS$ and since $q, S \gt 1$, $p$ must be a composite number, which contradicts the initial assumption that $p$ is prime. Therefore the supposition that $N$ is not prime must be incorrect and hence the number of digits must be prime if $p$ is prime

 

[Not anonymous]

15. How many ways can you tile a $2\times n$ rectangle with $1\times 2$ and $2\times 1$ rectangles? (IR)

Spoiler: Question 15

The answer I get is $F_{n+1}$, where $F_{i}$ are the Fibonacci numbers. The derivation is based on a recurrence relation. Let $f(m)$ be the function giving the number of ways to tile a $2 \times m$ rectangle using either of the 2 types of tiles ($2 \times 1$ or $1 \times 2$). The $2\times n$ rectangle consists of $2n$ "cells" (the smallest constituent rectangles of the $2 \times n$ rectangle), adjacent pairs (cells sharing a horizontal or vertical edge) of which are to be covered by a $1 \times 2$ or a $2 \times 1$ rectangular tile. Since all cells must be covered by tiles, we can start tiling from the leftmost cells and find the number ways to cover the remaining portion of the $2 \times n$ rectangle for each different way to tile the leftmost cells. As illustrated in the attached image:

1. The 2 leftmost cells (forming a $2 \times 1$ rectangle) can be covered by a $2 \times 1$ tile. This leaves a $2 \times (n-1)$ rectangle to be covered by tiles, and this region can be titled in $f(n-1)$ ways
2. The 4 leftmost cells (forming a $2 \times 2$ rectangle) can be covered by two $1 \times 2$ tiles. This leaves a $2 \times (n-2)$ rectangle to be covered by tiles, and this region can be titled in $f(n-2)$ ways

Thus, $f(n)$ reduces to:
$$
f(n) = \begin{cases}
1 & \text{if } n = 1 \\
2 & \text{if } n = 2 \\
f(n-1) + f(n-2) &\text{if } n \gt 2
\end{cases}
$$

$f(1), f(2), ..., f(n)$ therefore form a sequence very similar to the Fibonacci sequence but with $1, 2$ instead of $1, 1$ at the start, in other words, a Fibonacci sequence with a forward shift of index by 1, i.e. $f(n) = F_{n+1}$

 

[archaic]

Spoiler: Question 11

$$\frac{1}{P(x)}\underset{\infty}{\sim}\frac{1}{x^n}\Rightarrow\int_1^\infty\frac{dx}{P(x)}\text{ is of the same nature as }\int_1^\infty\frac{dx}{x^n}\\
\int_1^\infty\frac{dx}{x^n}=\frac{1}{n-1}+\lim_{t\to\infty}\frac{1}{(1-n)t^{n-1}}=\frac{1}{n-1}\text{ for }n\geq2$$
$$\int_1^\infty\frac{dx}{P(x)}=\int_1^\infty\frac{dx}{x+a_0}=\lim_{t\to\infty}\ln t=\infty\text{ for }n=1$$
Conclusion: The integral absolutely (since the leading coefficient is $1$ and $x\geq0$) converges for $n\geq2$.

 

[Infrared]

@Not anonymous Nice work. Everything looks right except for a small typo:

for $a \geq 1$, $(10^{a} - 1) = 9q$ where integer $q \gt 1$.

You should have $a>1$ here.

 

[archaic]

Spoiler: Question 13.b

$$\begin{align*}
\lim_{x\to\infty} \left[\ln(e^x + e^{-x}) - x\right]&=\lim_{x\to\infty} \left[\ln(e^x + e^{-x}) -\ln e^x\right]\\
&=\lim_{x\to\infty}\ln\left(\frac{e^x + e^{-x}}{e^x}\right)\\
&=\lim_{x\to\infty}\ln\left(1+\frac{1}{e^{2x}}\right)\\
&=0
\end{align*}$$

 

[archaic]

Spoiler: Question 10

This is more of an idea, I don't know how to formalize it, and whether it is correct (please correct me).
First of all, using the MVT, we know that $f'(x)=0$ for some $x=c\in(0,\,1)$.
Secondly, $f(x)=f'(x)$ cannot happen if $f(x)\geq0$ and is decreasing, or $f(x)\leq0$ and is increasing.
Suppose that $f(x)$ starts by increasing from $x=0$, then $f'(x)>f(x)$ but only up to some $x<1$ because of the MVT result, i.e $f'(x)$ must slow down until it becomes null. This tells us that at some $x$, we'll have $f(x)=f'(x)$ (this is like a worst case scenario, because $f(x)$ might go ahead of $f'(x)$ before the braking of the latter).
If $f(x)$ starts by decreasing from $0$, then we just consider $-f(x)$.

 

[fresh_42]

Spoiler: Question 11

$$\frac{1}{P(x)}\underset{\infty}{\sim}\frac{1}{x^n}\Rightarrow\int_1^\infty\frac{dx}{P(x)}\text{ is of the same nature as }\int_1^\infty\frac{dx}{x^n}\\
\int_1^\infty\frac{dx}{x^n}=\frac{1}{n-1}+\lim_{t\to\infty}\frac{1}{(1-n)t^{n-1}}=\frac{1}{n-1}\text{ for }n\geq2$$
$$\int_1^\infty\frac{dx}{P(x)}=\int_1^\infty\frac{dx}{x+a_0}=\lim_{t\to\infty}\ln t=\infty\text{ for }n=1$$
Conclusion: The integral absolutely (since the leading coefficient is $1$ and $x\geq0$) converges for $n\geq2$.

The case $n=1$ is correct, although sloppy in notation. You should integrate correctly before taking the limit.
The case $n=0$ is missing, although not really difficult.

What do you get, if you calculate $\displaystyle{\int_1^\infty \left|\dfrac{1}{(x-1)^3}\right|\,dx \;?}$ Here is $P(x)=x^3-3x^2+3x-1 \sim x^3$ for $x \to \infty,$ too.

"Is of the same nature" is not only un-mathematical, it's wrong, too.

 

[Adesh]

Question 7.

Spoiler

$$f(a +h) = f(a) + h f’(a) + \frac{h^2}{2} f”(a+\theta h)$$ let’s differentiate it with respect to $h$, $$ f’(a+h) = f’(a) + h f”(a+ \theta h) + \frac{\theta h^2}{2} f”’(a +\theta h) \\ \frac{f’(a+h) - f’(a)}{h} = f”(a+\theta h) + \frac{\theta h}{2} f”’(a+ \theta h)$$ if we take the limit as $h$ goes to $0$ we have $$ \lim_{h\to 0} \frac{f’(a+h) - f’(a)}{h} = f”(a+\theta h) + \frac{\theta h}{2} f”’(a +\theta h) \\ f”(a) = f”(a+\theta h) +\frac{\theta h}{2} f”’(a +\theta h)$$ Now, comes a very crucial step (a controversial too) since $f”’(x)$ is continuous at $a$ so we can easily prove that $f”(x)$ is continuous at $a$ hence we can write $\lim_{h\to 0} f”(a +h) = f”(a)$. Now, replacing $f”(a)$ with $f”(a+h)$ $$ \lim_{h \to} f”(a+h) - f”(a + \theta h) = \frac{\theta h}{2} f”’(a+\theta h)$$ Have a look at this $$ \lim_{h\to 0} \frac{f”(a+h) - f(a+\theta h)}{h(1-\theta)} = f”’(a+h) \\ \lim_{h\to 0} f”(a+h) - f”(a+\theta h) = h(1-\theta) f”’(a+h)$$ Now, let’s do the above substitution and write $$ h(1-\theta) f”’(a+h) = \frac{\theta h}{2} f”’(a+\theta h) \\ \textrm{using the fact that $f”’$ is continuous at $a$} f”’(a) - \theta f”’(a) = \frac{\theta}{2} f”’(a) \\ 1= \theta /2 + \theta \\ \theta = 2/3 $$ In the end, I got the wrong answer.

 

[archaic]

The case $n=1$ is correct, although sloppy in notation. You should integrate correctly before taking the limit.
The case $n=0$ is missing, although not really difficult.

What do you get, if you calculate $\displaystyle{\int_1^\infty \left|\dfrac{1}{(x-1)^3}\right|\,dx \;?}$ Here is $P(x)=x^3-3x^2+3x-1 \sim x^3$ for $x \to \infty,$ too.

"Is of the same nature" is not only un-mathematical, it's wrong, too.

Ugh, sorry about those two.
Is it about the lower bound? The questions says that the zeroes are all negative.
EDIT: Ah, you meant generally. Sorry, I am a bit sleepy.
By of the same nature, I meant that if one converges then the other does also.

 

[fresh_42]

The questions says that the zeroes are all negative.

That's why the statement in the problem is true and your proof wrong. You did not use this fact.

EDIT: Ah, you meant generally. Sorry, I am a bit sleepy.
By of the same nature, I meant that if one converges then the other does also.

That is no proof, and as my example showed, wrong. It is the same behaviour for large $x$, but nothing can be said what happens until then.

Hint: You should find an appropriate upper bound.

 

[archaic]

The case $n=1$ is correct, although sloppy in notation. You should integrate correctly before taking the limit.
The case $n=0$ is missing, although not really difficult.

What do you get, if you calculate $\displaystyle{\int_1^\infty \left|\dfrac{1}{(x-1)^3}\right|\,dx \;?}$ Here is $P(x)=x^3-3x^2+3x-1 \sim x^3$ for $x \to \infty,$ too.

"Is of the same nature" is not only un-mathematical, it's wrong, too.

À propos the remark on the integral. If we consider $\int_a^b$, then we suppose $a$ is in both functions' domain.

 

[archaic]

.

My bad, I thought that I didn't need to state it because it is mentioned explicitly. I'll try to rewrite it tomorrow, thank you!

 

[fresh_42]

À propos the remark on the integral. If we consider $\int_a^b$, then we suppose $a$ is in both functions' domain.

No. We could discuss Lebesgue integrals, but it is sufficient to say, that your argument doesn't use the fact that there are no poles, hence it is wrong.

 

[fresh_42]

My bad, I thought that I didn't need to state it because it is mentioned explicitly. I'll try to rewrite it tomorrow, thank you!

It is a bit tricky to make it waterproof. You have to get the starting values under control, not only the large ones.

 

[mathwonk]

#10: Hint:

even if f' is not continuous, it still has the intermediate value property, in common with continuous functions. Moreover, since f-f' is also a derivative (thanks Infrared!) hence either the problem is true or else f-f' is always either positive or negative on (0,1). Both these possibilities lead quickly to contradictions.

 

[Infrared]

This is more of an idea, I don't know how to formalize it, and whether it is correct (please correct me).
First of all, using the MVT, we know that $f'(x)=0$ for some $x=c\in(0,\,1)$.
Secondly, $f(x)=f'(x)$ cannot happen if $f(x)\geq0$ and is decreasing, or $f(x)\leq0$ and is increasing.
Suppose that $f(x)$ starts by increasing from $x=0$, then $f'(x)>f(x)$ but only up to some $x<1$ because of the MVT result, i.e $f'(x)$ must slow down until it becomes null. This tells us that at some $x$, we'll have $f(x)=f'(x)$ (this is like a worst case scenario, because $f(x)$ might go ahead of $f'(x)$ before the braking of the latter).
If $f(x)$ starts by decreasing from $0$, then we just consider $-f(x)$.

This isn't bad intuition to have, but there are a couple of issues. First of all, $f$ doesn't have to "start off" by either increasing or decreasing. For example, function $f(x)=x\sin(\frac{2\pi}{x}), f(0)=0$ oscillates infinitely often as $x\to 0$.

Next, even if $f$ does start off by increasing, you still have to justify why $f'(x)>f(x)$ near $x=0$.

You also have some loose language like "$f'(x)$ must slow down until it becomes null". You have to be careful that when formalizing this that you are not relying on $f'$ being continuous.

 

[QuantumQuest]

Question 7.

Spoiler

$$f(a +h) = f(a) + h f’(a) + \frac{h^2}{2} f”(a+\theta h)$$ let’s differentiate it with respect to $h$, $$ f’(a+h) = f’(a) + h f”(a+ \theta h) + \frac{\theta h^2}{2} f”’(a +\theta h) \\ \frac{f’(a+h) - f’(a)}{h} = f”(a+\theta h) + \frac{\theta h}{2} f”’(a+ \theta h)$$ if we take the limit as $h$ goes to $0$ we have $$ \lim_{h\to 0} \frac{f’(a+h) - f’(a)}{h} = f”(a+\theta h) + \frac{\theta h}{2} f”’(a +\theta h) \\ f”(a) = f”(a+\theta h) +\frac{\theta h}{2} f”’(a +\theta h)$$ Now, comes a very crucial step (a controversial too) since $f”’(x)$ is continuous at $a$ so we can easily prove that $f”(x)$ is continuous at $a$ hence we can write $\lim_{h\to 0} f”(a +h) = f”(a)$. Now, replacing $f”(a)$ with $f”(a+h)$ $$ \lim_{h \to} f”(a+h) - f”(a + \theta h) = \frac{\theta h}{2} f”’(a+\theta h)$$ Have a look at this $$ \lim_{h\to 0} \frac{f”(a+h) - f(a+\theta h)}{h(1-\theta)} = f”’(a+h) \\ \lim_{h\to 0} f”(a+h) - f”(a+\theta h) = h(1-\theta) f”’(a+h)$$ Now, let’s do the above substitution and write $$ h(1-\theta) f”’(a+h) = \frac{\theta h}{2} f”’(a+\theta h) \\ \textrm{using the fact that $f”’$ is continuous at $a$} f”’(a) - \theta f”’(a) = \frac{\theta}{2} f”’(a) \\ 1= \theta /2 + \theta \\ \theta = 2/3 $$ In the end, I got the wrong answer.

In the first expression you wrote in the beginning - which is given, you're missing a factorial.
Furthermore, there are various things I don't understand in your solution like this one:

$$\frac{f’(a+h) - f’(a)}{h} = f”(a+\theta h) + \frac{\theta h}{2} f”’(a+ \theta h)$$
if we take the limit as $h$ goes to $0$ we have $$ \lim_{h\to 0} \frac{f’(a+h) - f’(a)}{h} = f”(a+\theta h) + \frac{\theta h}{2} f”’(a +\theta h) \\ f”(a) = f”(a+\theta h) +\frac{\theta h}{2} f”’(a +\theta h)$$

and there are further more. As a hint, you can work through the given expression - maybe expand it(?), and see where it goes.

 

[Adesh]

In the first expression you wrote in the beginning - which is given, you're missing a factorial in it in order to be correct.

Well $2!$ is just 2.

And by the definition of derivative $$ \lim_{h\to 0} \frac{f’(a+h) - f’(a)}{h} = f”(a)$$

 

[archaic]

It is a bit tricky to make it waterproof. You have to get the starting values under control, not only the large ones.

Spoiler: Question 11

We have $n\in\mathbb{N}=\{0,\,1,\,2,\,...\}$ (just clarifying because I initially thought of $\mathbb{N}$ as not having $0$).
Since all the zeroes of $P(x)$ are negative, and its domain is $\mathbb{R}$, $\frac{1}{P(x)}$ is well defined for $x\geq0$.
Moreover, the sign of $\frac{1}{P(x)}$ is constant for $x\geq r_0$, where $r_0$ is the biggest zero of $P(x)$, and is the same as $P(x)$'s. As such, it is positive because $P(x)\underset{\infty}{\sim}x^n$ and $x^n\geq0$ when $x\to+\infty$.
The integral $\int_1^\infty\frac{dx}{P(x)}$ exhibits an improper behaviour only at $\infty$ because of what is stated above about the zeroes of $P(x)$. I will use this test for improper integrals'convergence:
If $f$ and $g$ are two (piecewisely) continuous and positive real functions on $[a,\,b)$, where $a\in\mathbb{R}$ and $b$ the same or is infinity, then, if $f(x)\underset{b}{\sim}g(x)$, then $\int_a^bf(x)\,dx$ converges $\Leftrightarrow\int_a^bg(x)\,dx$ converges.
$$\lim_{x\to\infty}\frac{\frac{1}{P(x)}}{\frac{1}{x^n}}=\lim_{x\to\infty}\frac{x^n}{P(x)}=\lim_{x\to\infty}\frac{x^n}{x^n\left(1+\frac{a_{n-1}}{x}+\frac{a_{n-2}}{x^2}+...+\frac{a_0}{x^n}\right)}=1$$
$$\int_1^\infty\frac{dx}{x^n}\text{ converges }\Leftrightarrow n>1\text{, by p-test}$$
Using the theorem stated above, $\int_1^\infty\frac{dx}{P(x)}$ converges if and only if $n>1$, or $n\geq2$.

 

[Adesh]

Question 13 a)

Spoiler

$$\lim_{x\to \pi/2} \frac{x-\pi/2}{\sqrt { 1-\sin x}} $$ Let $y = x - \pi/2$ $$\lim_{y\to 0} \frac{y}{\sqrt{ 1- \sin(y+ \pi/2)}} $$. $$ \lim_{y\to 0} \frac{y}{\sqrt {1- \cos y}}$$ $$\lim_{y\to 0} \frac{y}{\sqrt{2\sin^2 y/2}} $$
$$\lim_{y \to 0} \frac{y}{\sqrt 2 \sin y/2} \\ \lim_{y\to 0} \frac{
\frac{y}{y/2} }
{\sqrt 2\frac {\sin y/2}{y/2} } $$ The denominator in the above limit goes to $\sqrt2$ and the numerator cancels out to become 2 hence the answer is $\sqrt 2$.

 

[archaic]

Question 13 a)

Spoiler

$$\lim_{x\to \pi/2} \frac{x-\pi/2}{\sqrt { 1-\sin x}} $$ Let $y = x - \pi/2$ $$\lim_{y\to 0} \frac{y}{\sqrt{ 1- \sin(y+ \pi/2)}} $$. $$ \lim_{y\to 0} \frac{y}{\sqrt {1- \cos y}}$$ $$\lim_{y\to 0} \frac{y}{\sqrt{\sin^2 y/2}} $$
$$\lim_{y \to 0} \frac{y}{\sin y/2} \\ \lim_{y\to 0} \frac{
\frac{y}{y/2} }
{\frac {\sin y/2}{y/2} } $$ The denominator in the above limit goes to 1 and the numerator cancels out to become 2 hence the answer is $2$.

$\sqrt{\sin^2x}=|\sin x|$, and the limit is actually wrong. For the absolute value, you can see that it is not the same if you consider $x\to(\pi/2)^\pm$.

 

[Adesh]

$\sqrt{\sin^2x}=|\sin x|$, and the limit is actually wrong. For the absolute value, you can see that it is not the same if you consider $x\to(\pi/2)^\pm$.

Can you please explain a little more about which part you’re talking about?

 

[archaic]

Can you please explain a little more about which part you’re talking about?

Going from $\lim_{y\to 0} \frac{y}{\sqrt{\sin^2{y/2}}}$ to $\lim_{y \to 0} \frac{y}{\sin{y/2}}$ was wrong since approaching $0$ from the left is different from approaching it from the right when it comes to the sine function. Remember that $\sqrt{u^2}=|u|$.
You also made an error when you applied this $\sin^2{(x/2)}=\frac{1-\cos x}{2}$.

 

[Infrared]

#10: Hint:

even if f' is not continuous, it still has the intermediate value property, in common with continuous functions. Hence either the problem is true or else f-f' is always either positive or negative on (0,1).

I'm sure you're aware of this, but the set of functions satisfying the intermediate value property is not closed under addition. Here it should be fine anyway though, since $f+f'=(F+f)'$ where $F$ is a primitive for $f$.

 

[Adesh]

Going from limy→0y√sin2y/2limy→0ysin2⁡y/2\lim_{y\to 0} \frac{y}{\sqrt{\sin^2{y/2}}} to limy→0ysiny/2limy→0ysin⁡y/2\lim_{y \to 0} \frac{y}{\sin{y/2}} was wrong since approaching 000 from the left is different from approaching it from the right when it comes to the sine function. Remember that √u2=|u|u2=|u|\sqrt{u^2}=|u|

You mean that approaching from left would result in negative $\sin$ and approaching from right would result in $\sin$ being positive ?

 

[Adesh]

You also made an error when you applied this sin2(2x)=1−cosx2sin2⁡(2x)=1−cos⁡x2\sin^2{(2x)}=\frac{1-\cos x}{2}.

I corrected it upon your advice, thank you for that. But please correct that $\sin 2x$ to $\sin x/2$

 

[archaic]

You mean that approaching from left would result in negative $\sin$ and approaching from right would result in $\sin$ being positive ?

Yep!

 

[fresh_42]

Spoiler: Question 11

We have $n\in\mathbb{N}=\{0,\,1,\,2,\,...\}$ (just clarifying because I initially thought of $\mathbb{N}$ as not having $0$).
Since all the zeroes of $P(x)$ are negative, and its domain is $\mathbb{R}$, $\frac{1}{P(x)}$ is well defined for $x\geq0$.
Moreover, the sign of $\frac{1}{P(x)}$ is constant for $x\geq r_0$, where $r_0$ is the biggest zero of $P(x)$, and is the same as $P(x)$'s. As such, it is positive because $P(x)\underset{\infty}{\sim}x^n$ and $x^n\geq0$ when $x\to+\infty$.
The integral $\int_1^\infty\frac{dx}{P(x)}$ exhibits an improper behaviour only at $\infty$ because of what is stated above about the zeroes of $P(x)$. I will use this test for improper integrals'convergence:
If $f$ and $g$ are two (piecewisely) continuous and positive real functions on $[a,\,b)$, where $a\in\mathbb{R}$ and $b$ the same or is infinity, then, if $f(x)\underset{b}{\sim}g(x)$, then $\int_a^bf(x)\,dx$ converges $\Leftrightarrow\int_a^bg(x)\,dx$ converges.
$$\lim_{x\to\infty}\frac{\frac{1}{P(x)}}{\frac{1}{x^n}}=\lim_{x\to\infty}\frac{x^n}{P(x)}=\lim_{x\to\infty}\frac{x^n}{x^n\left(1+\frac{a_{n-1}}{x}+\frac{a_{n-2}}{x^2}+...+\frac{a_0}{x^n}\right)}=1$$
$$\int_1^\infty\frac{dx}{x^n}\text{ converges }\Leftrightarrow n>1\text{, by p-test}$$
Using the theorem stated above, $\int_1^\infty\frac{dx}{P(x)}$ converges if and only if $n>1$, or $n\geq2$.

I still don't like the inaccuracy of "behaves like" because it doesn't capture lower terms quantitatively. We have $\dfrac{1}{x^n}<\dfrac{1}{x^{n-1}}$, so why can we neglect those terms of lower orders? In other words: Why is $g(x)=x^{-n}$ suited, if $f(x)=P(x)^{-1}$ is actually bigger than $g(x)?$

There should be chosen a better function $g(x)$, which is actually greater than $x^{-n}$ and not only "near", and the estimation $\int 1/P(x) dx < \int g(x)dx$ should be accurate.

Your argument goes: "I have a function ($x^{-n}$), which is possibly smaller than $1/P(x)$, so it cannot guarantee convergence, but I don't care, since my error is small." However, you did not show that this heuristic is allowed.

 

[archaic]

I still don't like the inaccuracy of "behaves like" because it doesn't capture lower terms quantitatively. We have $\dfrac{1}{x^n}<\dfrac{1}{x^{n-1}}$, so why can we neglect those terms of lower orders? In other words: Why is $g(x)=x^{-n}$ suited, if $f(x)=P(x)^{-1}$ is actually bigger than $g(x)?$

There should be chosen a better function $g(x)$, which is actually greater than $x^{-n}$ and not only "near", and the estimation $\int 1/P(x) dx < \int g(x)dx$ should be accurate.

Your argument goes: "I have a function ($x^{-n}$), which is possibly smaller than $1/P(x)$, so it cannot guarantee convergence, but I don't care, since my error is small." However, you did not show that this heuristic is allowed.

It is actually a theorem:

Do you want me to prove it?

 

[fresh_42]

It is actually a theorem:
View attachment 259904
Do you want me to prove it?

You don't need the proof for a specific example. An idea, i.e. a better choice of $g(x)$ would do the job without the machinery. The proof must use a measure for the error, too, so this idea should be applied to the example. I have only 4 short lines for it, but it makes clear why this is true despite the fact that $1/x^n < 1/x^{n-1}$. I mean this is the crucial point of the entire question, and hiding it in a theorem doesn't really help understanding.

 

[archaic]

You don't need the proof for a specific example. An idea, i.e. a better choice of $g(x)$ would do the job without the machinery. The proof must use a measure for the error, too, so this idea should be applied to the example. I have only 4 short lines for it, but it makes clear why this is true despite the fact that $1/x^n < 1/x^{n-1}$. I mean this is the crucial point of the entire question, and hiding it in a theorem doesn't really help understanding.

Hm, maybe you're looking for $f(x)=\frac{c}{x^n}$ where $c>1$, so that $1/P(x)<f(x)$ for large $x$?
With that, I can also do a comparison test:
Let $g(x)=1/f(x)$. We know that after some $x=N>0$ we have $P(x)\geq g(x)$ since $\lim_{x\to\infty}\left(g(x)-P(x)\right)=-\infty<0$.
It follows that for $x\geq N$ we get $\frac{1}{P(x)}\leq\frac{c}{x^n}$, and so $\int_N^\infty\frac{dx}{P(x)}\leq\int_N^\infty c\frac{dx}{x^n}$.
If $n\geq2$, the second integral converges by the p-test, so the first also does by comparison test. And since $\int_1^N\frac{dx}{P(x)}$ converges (because $\frac{1}{P(x)}$ is well defined for $x\geq0$), $\int_1^N\frac{dx}{P(x)}+\int_N^\infty\frac{dx}{P(x)}=\int_1^\infty\frac{dx}{P(x)}$ also converges.
If $n=1$, then $\int_1^\infty\frac{dx}{x+a_0}=\int_{1+a_0}^\infty\frac{du}{u}$ which diverges by the p-test.
If $n=0$, then $\int_1^\infty dx$ surely diverges.

 

[fresh_42]

Hm, maybe you're looking for $f(x)=\frac{c}{x^n}$ where $c>1$, so that $1/P(x)<f(x)$ for large $x$?
With that, I can also do a comparison test:
Let $g(x)=1/f(x)$. We know that after some $x=N>0$ we have $P(x)\geq g(x)$ since $\lim_{x\to\infty}\left(g(x)-P(x)\right)=(1-c)/c<0$.
It follows that for $x\geq N$ we get $\frac{1}{P(x)}\leq\frac{c}{x^n}$, and so $\int_N^\infty\frac{dx}{P(x)}\leq\int_N^\infty c\frac{dx}{x^n}$.
If $n\geq2$, the second integral converges by the p-test, so the first also does by comparison test. And since $\int_1^N\frac{dx}{P(x)}$ converges (because $\frac{1}{P(x)}$ is well defined for $x\geq0$), $\int_1^N\frac{dx}{P(x)}+\int_N^\infty\frac{dx}{P(x)}=\int_1^\infty\frac{dx}{P(x)}$ also converges.
If $n=1$, then $\int_1^\infty\frac{dx}{x+a_0}=\int_{1+a_0}^\infty\frac{du}{u}$ which diverges by the p-test.
If $n=0$, then $\int_1^\infty dx$ surely diverges.

Nothing follows and how can we know what you claim without specifying the functions and constants you use? How do you find such a $c$, what are $f$ and $g$? You are sloppy and hand waving in your arguments.

We have to show that
$$
\int_1^\infty \left|\dfrac{1}{P(x)}\right|\,dx = \int_1^\infty \left|\dfrac{1}{x^n+a_{n-1}x^{n-1}+\ldots+a_0}\right|\,dx < \infty
$$
If you use a comparison with $\int_1^\infty \left|P(x)^{-1}\right|\,dx \leq \int_1^\infty g(x)\,dx <\infty$ then I want to know what $g(x)$ is and why the inequality holds. The argument is obviously wrong if we integrate over zeroes of $P(x)$. Where did you use that we do not have this case, except within the theorem somewhere? E.g. $g(x)= x^n > x^n-x^2 =:P(x)$ does not work. So which $g(x)$ can we use and why?