biplab93
- 2
- 0
I was solving this paper, but got stuck on this question, and it's been bugging me endlessly. I don't know what I'm missing. Here's the question:
A rod of 20 dia is fixed to the ceiling of a roof on one end. A rotor of 50 kg mass is attached to the free end with bearings. The CG of the rotor is 10 mm away from the shaft axis. The rotor is rotating at 600 rpm. The max tensile stress (in N/Sq.mm) in the rod is nearly equal to
A. pi/2
B. 200pi
C. 300pi
D. 400pi (correct answer)
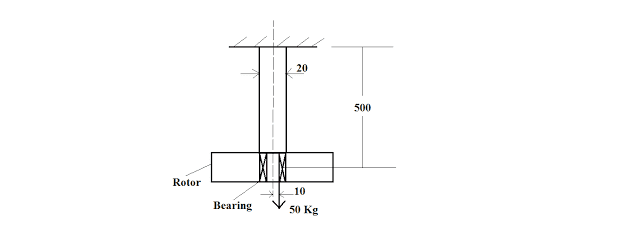
Because of the bearings, there will be no torsional load on the rod (right?). That only leaves out the eccentric tensile load. So I converted that into an axial tensile load and a bending moment (50g*10 Nmm), and the resulting bending stress is: 1.6 (axial) + 6.3 (bending) N/mm^2 = 7.9. (Bending stress = M*y/I. y=max distance from neutral axis)
That's a far cry from 400pi. I don't know how the length of the rod (500mm) or the speed of the rotor (600rpm) will be incorporated, or if they will be needed at all.
Help will be much appreciated. Thanks in advance.
A rod of 20 dia is fixed to the ceiling of a roof on one end. A rotor of 50 kg mass is attached to the free end with bearings. The CG of the rotor is 10 mm away from the shaft axis. The rotor is rotating at 600 rpm. The max tensile stress (in N/Sq.mm) in the rod is nearly equal to
A. pi/2
B. 200pi
C. 300pi
D. 400pi (correct answer)
Because of the bearings, there will be no torsional load on the rod (right?). That only leaves out the eccentric tensile load. So I converted that into an axial tensile load and a bending moment (50g*10 Nmm), and the resulting bending stress is: 1.6 (axial) + 6.3 (bending) N/mm^2 = 7.9. (Bending stress = M*y/I. y=max distance from neutral axis)
That's a far cry from 400pi. I don't know how the length of the rod (500mm) or the speed of the rotor (600rpm) will be incorporated, or if they will be needed at all.
Help will be much appreciated. Thanks in advance.