cwill53
- 220
- 40
- Homework Statement
- Determine the mean force in a piston rod connecting pistons in two tandem cylinders of a steam engine if the diameters of the pistons are $$D_{1}$$=12.5 in., $$D_{2}$$=24in., the diameters of the piston rods are $$d_{1}$$=2.5in, $$d_{3}$$=4 in., and the mean steam pressures $$p_{1}$$= 135$$lb/in^{2}$$, $$p_{2}$$= 35.5$$lb/in^{2}$$, and $$p_{3}$$= 1.5$$lb/in^{2}$$.
- Relevant Equations
- $$p=\frac{\vec{F}}{A}$$
I found the correct solution using the equation that relates force and pressure, but I don't REALLY understand what the question is asking and what is actually going on in the machine. I want a better understanding of everything that's going on, not just an answer. Below is a clear diagram and a clear sheet of my work.
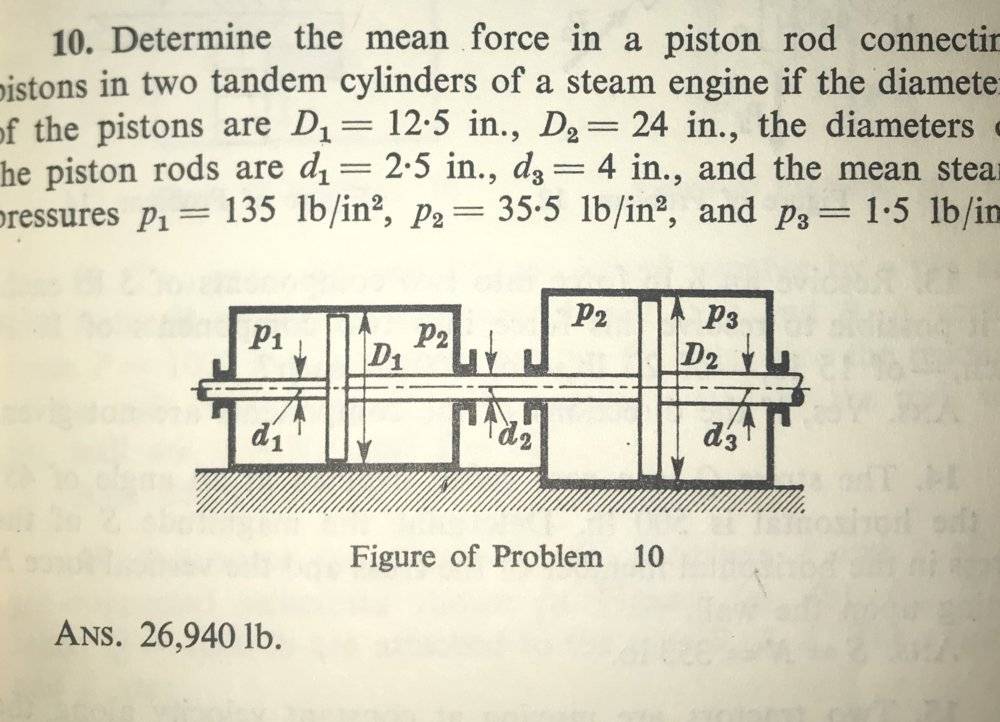

One issue I had was that the diameter of the piston rod d2 is not given. Maybe it was a typo? I don't know. But I made a guess and assumed that it was the average between d1 and d3. Another thing I don't get is what is meant by "mean force," and what exactly is happening in each section of the piston.
One issue I had was that the diameter of the piston rod d2 is not given. Maybe it was a typo? I don't know. But I made a guess and assumed that it was the average between d1 and d3. Another thing I don't get is what is meant by "mean force," and what exactly is happening in each section of the piston.