Mean Radius of Annulus with Bolt Hole Pattern

[j0nr]

Hello all,

I am trying to remember (I did it in Uni) how to calculate the effective mean radius of an annulus that contains a pattern of holes on a PCD.

Consider the following image (pinched from: https://www.solenoid-valves.com/ ):

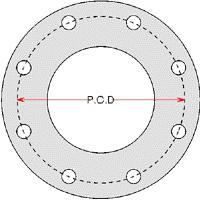
If one was to vary the value of PCD, then the effective mean radius would change (I believe). But how do you work out the effective mean radius for purposes of friction torque transmission calcs?

Thanks in advance,

Jon

 

[j0nr]

Thought I might add...as I've been thinking about it...depending on the stiffness of the materials, if this is considered a constant pressure application, then mean rad would just be:

\frac{2}{3} ( \frac{ (r_1^3-r_2^3) }{ (r_1^2-r_2^2) } )

...regardless of hole pattern...I think.