ashishsinghal
- 462
- 0
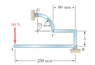
Determine the reactions at B and D when b = 60mm ?
(Diagram is attached)
Since B and D are hinged we don't know the direction as well as magnitude of the reaction forces at B and D. Hence we have 4 unknowns (Bx, By, Dx, Dy).
But I can't find 4 independent equations. I got three by ƩFx= 0, ƩFy= 0 and moment about B = 0. Where is the 4th equation. Please help.
(Diagram is attached)
Since B and D are hinged we don't know the direction as well as magnitude of the reaction forces at B and D. Hence we have 4 unknowns (Bx, By, Dx, Dy).
But I can't find 4 independent equations. I got three by ƩFx= 0, ƩFy= 0 and moment about B = 0. Where is the 4th equation. Please help.