teh_dude
- 11
- 0
Mesh Current: Cannot see my mistake in my approach?
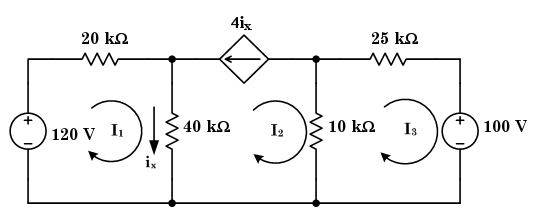
Find currents I1, I2, and I3 using Mesh Current Analysis in this circuit:
KVL
Initial equations:
Mesh 1: -120 + 20k(I1) + 40k(I1 - I2) = 0
Mesh 2: 40k(I2 - I1) - 4ix + 10k(I2 - I3) = 0
Mesh 3: 10k(I3 - I2) + 25k(I3) + 100 = 0
As seen in the circuit, ix = 40k(I1 - I2), so the equation for Mesh 2 can be rewritten as:
New Mesh 2: 40k(I2 - I1) - 160k(I1 - I2) + 10k(I2 - I3) = 0
After rearranging and consolidating, I come up with this system ready to put in an augmented matrix:
60k(I1) - 40k(I2) + 0(I3) = 120
-200k(I1) + 210k(I2) - 10k(I3) = 0
0(I1) - 10k(I2) + 35k(I3) = -100
The answer must be submitted online (yay for unlimited attempts!), and in this instance, must be in mA.
I get the following using the "rref()" function in my TI-84:
I1 = 5.3548387 mA
I2 = 5.0322581 mA
I3 = -1.4193548 mA
I get the following different answers by hand:
I1 = .003168316832 mA
I2 = 2.3762376 mA
I3 = 21.7821782 mA
All of these are incorrect according to the website, but I don't see an error in my equations (although my attempt by hand probably has errors).
FYI, this is an extra credit problem that I am doing solely for extra practice before the test. Generally I'm pretty proficient at this, but this one just isn't making any sense to me--either that or maybe I'm right and the site's wrong? lol...
Homework Statement
Find currents I1, I2, and I3 using Mesh Current Analysis in this circuit:
Homework Equations
KVL
The Attempt at a Solution
Initial equations:
Mesh 1: -120 + 20k(I1) + 40k(I1 - I2) = 0
Mesh 2: 40k(I2 - I1) - 4ix + 10k(I2 - I3) = 0
Mesh 3: 10k(I3 - I2) + 25k(I3) + 100 = 0
As seen in the circuit, ix = 40k(I1 - I2), so the equation for Mesh 2 can be rewritten as:
New Mesh 2: 40k(I2 - I1) - 160k(I1 - I2) + 10k(I2 - I3) = 0
After rearranging and consolidating, I come up with this system ready to put in an augmented matrix:
60k(I1) - 40k(I2) + 0(I3) = 120
-200k(I1) + 210k(I2) - 10k(I3) = 0
0(I1) - 10k(I2) + 35k(I3) = -100
The answer must be submitted online (yay for unlimited attempts!), and in this instance, must be in mA.
I get the following using the "rref()" function in my TI-84:
I1 = 5.3548387 mA
I2 = 5.0322581 mA
I3 = -1.4193548 mA
I get the following different answers by hand:
I1 = .003168316832 mA
I2 = 2.3762376 mA
I3 = 21.7821782 mA
All of these are incorrect according to the website, but I don't see an error in my equations (although my attempt by hand probably has errors).
FYI, this is an extra credit problem that I am doing solely for extra practice before the test. Generally I'm pretty proficient at this, but this one just isn't making any sense to me--either that or maybe I'm right and the site's wrong? lol...