Min Force to keep from Slipping

[SnowboardNerd]

Homework Statement

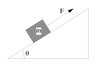
A block weighing 70.6 N rests on a plane inclined at 26.9o to the horizontal. The coefficients of static and kinetic friction are 0.23 and 0.14 respectively. What is the minimum magnitude of the force F, parallel to the plane, that will prevent the block from slipping?

Picture Include!

Homework Equations

F=m*a

us*Fn = static friction

The Attempt at a Solution

I split force of gravity into its components. (Y DIRECTION). I found the Fn to equal mg cos theta

decided that for the X DIRECTION to do

F - usFn - mg sin theta = m * a... then I made A = 0... which made the [ ...left side... = 0 ]

Then I solved for F... which gave me 48.1799 N.

But unfortunately this is wrong. Any Ideas? Thank you!

 

[SnowboardNerd]

More of my attempt...
__________________
Y Direction:

Sum F = M * A
Fn-mg = 0
Fn = mgcosTheta <---- I got this from breaking gravity into it's components.

_________________

X Direction:

Sum F = M * A
F - Static Friction - mgSinTheta = 0
F = uS*Fm - mgsinTheta

_________________

Can you please give me some direction? Thank you!

 

[grzz]

Fn = mgcosTheta <---- I got this from breaking gravity into it's components.

F - Static Friction - mgSinTheta = 0

First equation is OK.

Now you were asked for the minimum force. Hence the block will tend to slip DOWNWARDS. Therefore frictional force is UP the plane.
If you correct the 2nd equation you are OK.

 

[SnowboardNerd]

F - (0.23)(70.6cos(26.9)) - (70.6)sin(26.9)) = 0

F - Kintic Friction - mgSinTheta = 0

^^ Is that what you meant?

Thank you.

 

[issacnewton]

what is Fm ? kinetic friction doesn't come into the picture

 

[SnowboardNerd]

I think Fn = W... so in the beginning when they said that it's W = 70.6 that means that Fn = 70.6?

 

[SnowboardNerd]

I thought you ment Fn... I'm not sure what the variable Fm stands for

 

[grzz]

F - (0.23)(70.6cos(26.9)) - (70.6)sin(26.9)) = 0

No that is not what I meant.
The first minus must be changed into plus since friction is up in same direction as the applied force F.
All is at rest so kinetic friction is out.

 

[issacnewton]

the downward component of the weight is more than the maximum static frictional force...
so you will need to apply the amount of force in the upward direction, which is the difference between the two

 

[SnowboardNerd]

F + (0.23)(70cos(26.9)) - (70.6sin(26.9)) = 0

F = 17.6 N

Yeah! Thank you very much!I have another thread open too if you would be kind enough to help!

https://www.physicsforums.com/showthread.php?p=3529346&posted=1#post3529346

 

[SnowboardNerd]

F + (0.23)(70cos(26.9)) - (70.6sin(26.9)) = 0

F = 17.6 N

Yeah! Thank you very much!


I have another thread open too if you would be kind enough to help!

https://www.physicsforums.com/showthread.php?p=3529346&posted=1#post3529346

 

[grzz]

the downward component of the weight is more than the maximum static frictional force...
so you will need to apply the amount of force in the upward direction, which is the difference between the two

Correct!