ehilge
- 160
- 0
Homework Statement
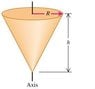
Calculate the moment of inertia of a uniform solid cone about an axis through its center. The cone has mass M and altitude h. The radius of its circular base is R. (see attached photo)
Homework Equations
I know I need to somehow use the equation I=\intr<sup>2</sup>dm
also, I have an equation from my proffessor, dm=\rhodv I'm not sure if I need this though since its unifrom density so it doesn't seem like \rho should matter.
The Attempt at a Solution
I don't have a solution right now. I know the answer is 3/10 MR2 but I don't know how to het there. From class, since we did some examples, I think I need an equation that has a triple integral in it but I don't know what to integrate and to where.
Thanks for your help. Also, if you have any general suggestions on how to complete moment of inertia problems like this that would be great. I know we're going to be doing a lot of them.
Thanks again!