How Do You Calculate Initial Current in a Multi-Capacitor RC Circuit?

AI Thread Summary
To calculate the initial current in a multi-capacitor RC circuit, first determine the initial voltages across both capacitors when switch S2 is closed. The 2-microfarad capacitor is discharging while the 6-microfarad capacitor is charging, which influences the current flow. The initial current can be found using the equation I = V/R, where V is the voltage across the resistor at that moment. Understanding the voltage across each capacitor is crucial for accurate calculations. The discussion emphasizes the importance of analyzing both capacitors' states to find the initial current effectively.
jforce93
Messages
26
Reaction score
0

Homework Statement



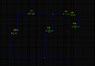
The circuit used in this problem is attached as an image. I made this in gEDA (the circuit is from the homework problem, I just didn't feel like using a scanner to get the image)
The 2-microfarad capacitor shown in the circuit attached is fully charged by closing switch S1 and keeping switch S2 open, thus connecting the capacitor to the 2,000 Volt power supply. At a later time, switch S1 is opened. Switch S2 is then closed. The 6-micro farad capacitor is initially uncharged. Determine the initial current in teh resistor the instant after switched S2 is closed.

Homework Equations



I = \frac{-q<sub>0</sub>}{RC} e-t/RC (discharging a capacitor)
V = IR

The Attempt at a Solution



I'm not sure how to go about this, and I don't have an answer key. Should I calculate using the fact that the 2 micro farad capacitor is discharging, or the fact that the 6 microfarad capacitor is charing?
Thanks!

Jordan

 

Attachments

  • circuit final.png
    circuit final.png
    1.7 KB · Views: 618
Last edited:
Physics news on Phys.org
Sorry, forgot to attach a picture of the circuit. Will do that soon.
 
To find the initial current through the resistor, find the initial potential across that resistor. What are the initial voltages on the two capacitors at the instant S2 is closed?
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Calculating Charge and Time in a Discharging RC Circuit
Replies
3
Views
2K
Need help finding current on RC circuit
Replies
5
Views
7K
RC Circuit with parallel resistor
Replies
6
Views
3K
How Does a Capacitor Charge to Negative Voltage in an RC Circuit?
Replies
20
Views
4K
Solve RC Circuit Problem: 45V -> 10V in 4.21ms
Replies
4
Views
8K
Energy dissipated in the resistors in a 2 mesh RC circuit
Replies
1
Views
2K
How Do You Calculate Capacitance in a DC Circuit with a Fully Charged Capacitor?
Replies
3
Views
1K
Current of RC Circuit After Switch is Opened
Replies
3
Views
3K
Complex RC Circuit - Multiple Resistors
Replies
10
Views
6K
Time Constant, Maximum Charge, and Current in an RC Circuit
Replies
11
Views
3K

Hot Threads

Recent Insights

Back
Top