Need help to analyze the circuit for a HW problem

[Parad0x88]

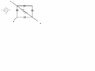
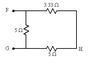
The one of the left is the original, the one on the right I re-drew by changing the orientation with paint (the lines are the resistance)

It's the first time that I see a circuit with a resistance in-between in a diagonal fashion. Can the top and bottom face, as well as the left and right face, still be considered in parallel despite the resistance crossing diagonally in front of all of them?

 

[256bits]

Hello.
What do parallel resistances have in common - voltage drop or current through them?What do series resistances have in common - voltage drop or current through them?

 

[Parad0x88]

Hello.
What do parallel resistances have in common - voltage drop or current through them?What do series resistances have in common - voltage drop or current through them?

Parallel current drop through them, while series voltage drop through them

(Don't take offense) I don't know if this is the first question you will ask me of a series to help me understand, or if this was meant to shed enough light, but I still don't understand

The problem gives no voltage or no current, it only asks: In the figure below find the equivalent resistance between a) points F and H and b) points F and G. All five resistances are 5 ohm. Here's my attempt at analyzing:

So for me, if I assume they are all in series (giving that the diagonal prevents a parallel combination) than the sum of R's are simply 5+5+5+... However, this seems to simple. So if I assume that parallel is possible, then I would have:

A) 2.5 ohm
Top of the diagonal are in series, thus R = 10 ohm
Bottom of the diagonal are in series, thus R = 10 ohm
All three will now be in parallel (I guess it would make sense by the way they are combined), thus: 1/10 + 1/10 + 1/5 = .1 + .1 + .2 = .4 = 1/.4 = 2.5 ohm

B) ? ohm
Top of the diagonal are in series, thus R = 10 ohm
It is in parallel with the diagonal, thus R = 1/10 + 1/5 = 3/10 = .3 = 1/.3 = 3.33 ohm

Not sure at this point

 

[Parad0x88]

Any further insight on this? I came back to it but I have a very hard time visualizing, I think it's because it's the first example where I have a diagonal, it really confuses me

 

[gneill]

Parallel current drop through them, while series voltage drop through them

(Don't take offense) I don't know if this is the first question you will ask me of a series to help me understand, or if this was meant to shed enough light, but I still don't understand

The problem gives no voltage or no current, it only asks: In the figure below find the equivalent resistance between a) points F and H and b) points F and G. All five resistances are 5 ohm. Here's my attempt at analyzing:

So for me, if I assume they are all in series (giving that the diagonal prevents a parallel combination) than the sum of R's are simply 5+5+5+... However, this seems to simple. So if I assume that parallel is possible, then I would have:

Okay, you've finally told us what the resistance values are; 5 Ohms each.

A) 2.5 ohm
Top of the diagonal are in series, thus R = 10 ohm
Bottom of the diagonal are in series, thus R = 10 ohm
All three will now be in parallel (I guess it would make sense by the way they are combined), thus: 1/10 + 1/10 + 1/5 = .1 + .1 + .2 = .4 = 1/.4 = 2.5 ohm

That's a fine analysis; the result looks good.

B) ? ohm
Top of the diagonal are in series, thus R = 10 ohm
It is in parallel with the diagonal, thus R = 1/10 + 1/5 = 3/10 = .3 = 1/.3 = 3.33 ohm

Not sure at this point

Time to redraw the circuit then. You're left with a 3.33 Ohm resistor and two five Ohm resistors:

Don't let diagonal lines or "artistic" touches fool you on circuit diagrams. The only thing that matters is the actual interconnections of the components. So long as those are preserved, you can move things about, bend wires, rotate things, etc., to your heart's content.

 

[Parad0x88]

Okay, you've finally told us what the resistance values are; 5 Ohms each.

That's a fine analysis; the result looks good.

Time to redraw the circuit then. You're left with a 3.33 Ohm resistor and two five Ohm resistors:

Don't let diagonal lines or "artistic" touches foll you on circuit diagrams. The only thing that matters is the actual interconnections of the components. So long as those are preserved, you can move things about, bend wires, rotate things, etc., to your heart's content.

Thanks, very helpful! I got 3.125 ohm for the last one. My question is, why do I treat A differently than B as the order that I put them in series/parallel? I just realized that both A and B I could have inversed the steps and to me it doesn't make a difference, although it obviously has one that I do not grasp... This is pure exam material, so any input would be great! :D

 

[gneill]

The difference is that the nodes between which you want to find the net resistance are different for the two cases and afford different opportunities (often based upon circuit symmetry) to proceed.

There are often several paths to solution, like adding numbers in a different order to find a total. Sometimes you can take advantage of obvious symmetries to get to the result faster. In the first instance where the nodes in question are F and H, the symmetry makes it clear that the outside paths are in parallel with the central diagonal. It's also clear that the two outside paths have the same resistance (both are twice 5 Ohms). So their parallel resistance will be 10 || 10, or 5 Ohms. That 5 Ohms is thus in parallel with the 5 Ohm diagonal, rendering 5 || 5 or 2.5 Ohms. So symmetry can be a real timesaver. Of course you could also slog through first putting one of the outside paths in parallel with the diagonal, giving 10 || 5 = 3.333 Ohms, and then putting that in parallel with the other outside path, so calculating 3.333 || 10 = 2.5 . Same result but more brainsweat.