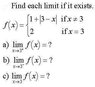Jonny B
- 2
- 0
1. http://s24.postimg.org/jdd9l8ayd/q8q_a.jpg
2. http://s24.postimg.org/z04iyloqd/q1q_a.jpg
3. http://s24.postimg.org/oeknmliet/q2q.jpg
4. http://s24.postimg.org/puw64qlbp/q6q.jpg
Questions are in the links above.
I completed 4 out of the 8 problems. I just don't know how to do these (As in I know what I'm doing is wrong).
2. http://s24.postimg.org/z04iyloqd/q1q_a.jpg
3. http://s24.postimg.org/oeknmliet/q2q.jpg
4. http://s24.postimg.org/puw64qlbp/q6q.jpg
Questions are in the links above.
I completed 4 out of the 8 problems. I just don't know how to do these (As in I know what I'm doing is wrong).
Last edited by a moderator: