stiwi_xyz
- 13
- 2
- Homework Statement
- I've been trying to figure this out for a while now so can someone give me a few pointers on this?
- Relevant Equations
- KVL, KCL, Ohm's Law
Consider the resistor network shown in Figure 1-1, where 𝑅1=2𝑘Ω and 𝑅2=5𝑘Ω.
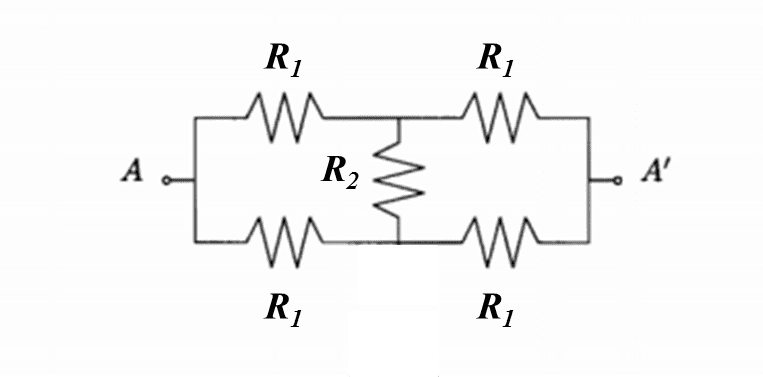
(a) Calculate the numerical value of the single equivalent resistance, in 𝑘Ω, as seen from the terminals 𝐴−𝐴′. Express your answer to two decimal places.Next, consider the circuit shown in Figure 1-2, where 𝑉=30𝑉 and 𝑅3=3𝑘Ω:
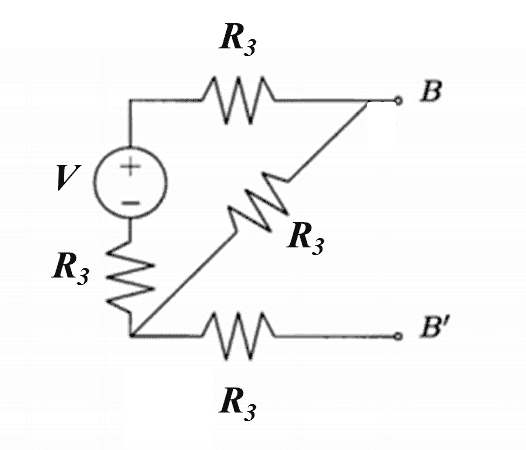
This circuit can be reduced into its Thevenin equivalent, shown in Figure 1-3:
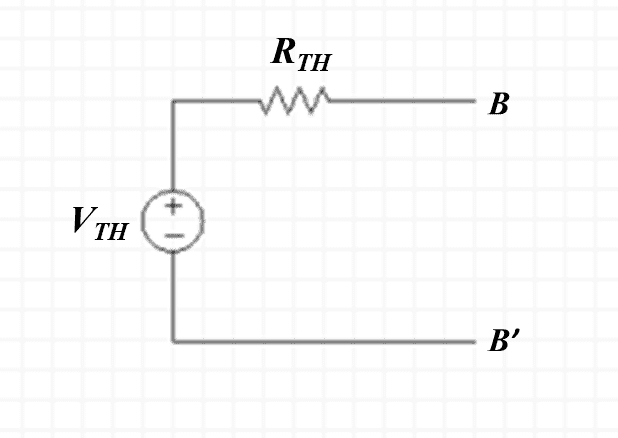
(b) Calculate the numerical value of the single Thevenin voltage, in Volts, as seen from the terminals 𝐵−𝐵′.(c) Calculate the numerical value of the single Thevenin resistance, in 𝑘Ω, as seen from the terminals 𝐵−𝐵′.
(a) Calculate the numerical value of the single equivalent resistance, in 𝑘Ω, as seen from the terminals 𝐴−𝐴′. Express your answer to two decimal places.Next, consider the circuit shown in Figure 1-2, where 𝑉=30𝑉 and 𝑅3=3𝑘Ω:
This circuit can be reduced into its Thevenin equivalent, shown in Figure 1-3:
(b) Calculate the numerical value of the single Thevenin voltage, in Volts, as seen from the terminals 𝐵−𝐵′.(c) Calculate the numerical value of the single Thevenin resistance, in 𝑘Ω, as seen from the terminals 𝐵−𝐵′.
Last edited by a moderator: