Newton Laws - Finding a constant

[bluewood]

Homework Statement

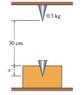
To find the stiffness of a material, a block of that material is placed 30 cm under a metallic cone with 0.3 kg; the cone is free falling from rest, penetrating a distance x in the block until it stops. It is known that when the cone penetrates in the block the force of the block exerced on the cone is kx² where k is a constant that depends on the stiffness to penetration of the material; if the cone penetrates a distance x = 5 cm, find the value of the constant k.

An added restriction that I'm adding to the problem is to not use the relations between Work and Energy (at least directly) -> that subject wasn't approached yet.

Homework Equations

The derivatives of x(t) and v(t), and:
a = v\frac{dv}{dx}
F = m a

The Attempt at a Solution

According to the solutions and to the Work-Energy relations, k should be 24696 N/m². But I've tried several times and the values don't match:
F - W = m a
k {x}^{2} - 9.8 m = m a
k {x}^{2} - m 9.8 = m v \frac{dv}{dx}
\int_{0.05+0.3}^{0}k {x}^{2} - m 9.8\,dx = \frac{1}{2} ({0}^{2}-{0}^{2})
-\frac{343 k - 24696}{24000} = 0
k = 72

 

[kuruman]

Check your limits of integration. You cannot put both forces under the same integral. Gravity acts over the entire distance of 0.35 cm, but the "stiffness" force acts over 0.05 cm only.

 

[bluewood]

Thanks for the remark, I've managed to find the correct solution. I've tried several times before, and one of the steps that was confusing me before was when I was calculating the speed of the cone before hitting the cone.

If I considered a frame of reference where g = -9.8 m/s², the speed before hitting the block would be an imaginary value, but using a different frame where g = +9.8, the speed would be a real value - ignoring those facts the numeric value is the same. It is kinda awkward, since using the first referential most of the people would think their calculations were wrong (EDIT: see the end of this post).

The other thing was the net force acting on the cone, wether the normal reaction existed or not. Anyway, here's the calculations in case anyone wants the solution (I'm considering "up" as positive and x = 0 when the cone is inside the block):

1. Finding the speed of the cone before hitting the block

v\frac{dv}{dx} = -9.8

\int_{0}^{v_f}v\,dv = \int_{x+0.30}^{x}-9.8\,dx

\left[ \frac{v^2}{2} \right]_{0}^{v_f} = \left[-9.8 x \right]_{x+0.30}^{x}

{v_f}^2 = 2 \times -9.8 \times (x - (x + 0.30))

v_f = \pm \sqrt{5.88}

For this case we're interested in the negative value.


2. Finding k

F - W = m a

kx^2 - 9.8 m = m a

\int_{0}^{0.05}(kx^2 - 9.8 m)\,dx = \int_{0}^{- \sqrt{5.88}} mv\,dv

\left[ \frac{kx^3}{3} - 9.8mx \right]_{0}^{0.05} = \left[ \frac{mv^2}{2} \right]_{0}^{-5.88}

\frac{k}{24000} - 0.49m = 2.94 m

k = 82320 m

Since m = 0.3 kg:

k = 24696 N/m^2

EDIT: Corrected a small mistake in the right integral of step 1. The speed value is always real no matter what frame of reference is chosen.

 

[kuruman]

If I considered a referential where g = -9.8 m/s², the speed before hitting the block would be an imaginary value, but using a different referential where g = +9.8, the speed would be a real value - ignoring those facts the numeric value is the same. It is kinda awkward, since using the first referential most of the people would think their calculations were wrong.

The correct answer should be independent of your frame of reference. In other words, the block will hit the material with the correct speed regardless of whether you (or anyone else) choose "up" as positive or "down" as positive.

The kinematic equation to use is

2 a Δx = v² - v₀²

with v₀ = 0, we get
v=\sqrt{2a\Delta x}

Note that both the displacement and the acceleration vectors point "down". If we choose "down" as positive, then both quantities under the radical are positive and there is no problem. If we choose "up" as positive, then both quantities under the radical are negative, however their product is a positive number and there still is no problem.

 

[bluewood]

You are correct. Actually, that imaginary value in my previous calculations in the speed was due to an error in the limits of integration. I've tried several (fixed) frames of reference and all yielded the correct value for the speed.

Thanks