MyNameIsNicholas
- 4
- 0
Member advised to use the homework template for posts in the homework sections of PF.
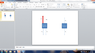
These buckets are being suspended. The cords have no mass and each bucket is 3.5 kg.
a.) Find the tension in the upper cord (T1) and the lower cord (T2)
b.) If the apparatus is pulled upwards from the top of the upper cord, what are the new tensions of each cord?
I understand the first part. The force diagrams consist of:
(Upper Bucket): T1 upwards, T2 downwards, and Fg downwards
(Lower Bucket): T2 upwards and Fg downwards
However, when the apparatus accelerates upwards, the tensions in both cords increases. This makes sense physically but in the force diagram isn't force applied (causing acceleration) going upwards? And if that were the case, then force applied would counter-intuitively decrease the tension within the cords. Can someone graciously clear this up for me?