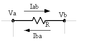gl0ck
- 85
- 0
Homework Statement
The Attempt at a Solution
According to the similar problem
Node X:
I1=(22-Vx)/66
I2=(66-Vx)/44
Il=Vx/264
I3=I1+I2+Il
Node Y:
I4=Vy/240
I5=6
I4=I3+I5
After the calculations I get 1.08 for Vx, which I think is wrong.
Thanks