- #1
celect
- 43
- 0
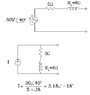
Can someone direct me to a tutorial for solving network
nodal voltages.
Also need to learn how to convert voltage source to a current source.
nodal voltages.
Also need to learn how to convert voltage source to a current source.