theuniverse
- 53
- 0
Homework Statement
Derive an expression for the gain Vout/Vin. Express your answer in the form of A+jB.
Homework Equations
The Attempt at a Solution
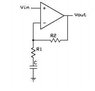
If C is the capacitor in series with R1, gain = 1 + R2/[R1 + 1/(jwC)]. It says to express it in the form of A (real)+ jB (imaginary), but I'm not sure how to make the conversion from my solution of gain to the form of A+jB.
Any help is appreciated.
Edit: Figured that I can rewrite it as gain = 1 + R2/[R1 - j/wC] and I tried multiplying by the conjugate but I still can't get it...
Attachments
Last edited: