Online Course Work Question - Dynamics

[RoyalewithCh33s3]

Hello everyone, I'm sorry if a question like this has been posted before, but I am trying to get my online work done for tonight and I have come across two problems that I just can't get past. I have gotten far into the problems but the website I enter values in on says theyre wrong. I appreciate any help I can get.

Question 1:

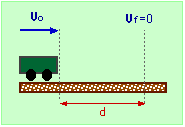
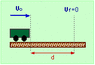
On a level road with its brakes on, the shortest distance in which a car traveling with 98 km/hr can stop is 92 m. The shortest stopping distance occurs when the driver uses anti-lock brakes, which means that the car brakes without skidding.

I found |a| to be: 4.027 m/s^2

Next it asks for b) What is the coefficient of static friction between the tires and the pavement?

I looked up the coefficient of friction for concrete and rubber and it says 1. Now when I put that in it says it's wrong. I was wondering how its possible to figure out a problem like this with no value for mass.

Question 2:

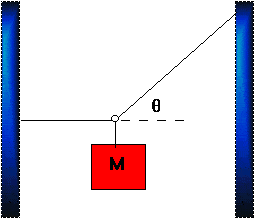
A block of mass M = 15 kg is suspended at rest by two strings attached to walls, as shown in the figure. The left string is horizontal and the right string makes an angle q = 50° with the horizontal. What is the tension in the left string? (Assume the ring where the strings come together is massless.)

Ok, this one I thought I had the right answer after working through it but the site says I'm wrong. Here's what I did:

15kg=147.15N

Since there are two strings holding up the block, 147.15/2=73.58

That means that the T in the y direction of the right string is 73.58N.

Then TRy=73.58/sin50 or 96.045 N

Now if I might be mistaken but that force doesn't really matter because what I can use is the T on the right string in the x direction is equal to the T on the left string in the x direction (because the system is in equilibrium).

So: F in x direction on the right string= 73.58/tan50

Which means that the T on the left string= 61.74 N

I might be missing a key concept here, but any help with this would be appreciated. Thanks! (And go easy on my please, I know what its like to read posts by newbies.)

 

[RoyalewithCh33s3]

Yeah, I've been looking around online and I haven't seen any equation or group of equations to figure out friction without a mass.

 

[Chi Meson]

You have the acceleration. Newton's 2nd law says what about acceleration? (hint: consider the frictional force to be the only force on the car tires)

 

[RoyalewithCh33s3]

F=ma

Ok, I was trying to use that but don't we have two unknowns here?

We don't know m, and we can't get the FF=(mu)FN

So how can I use the Force of friction on the tires if I have no mass and only acceleration?

 

[RoyalewithCh33s3]

Oh, and there's an update...I got the second problem by not dividing the force in the y direction by two. It was a pure guess and check, so if someone can explain why that would be greatly appreciated.

 

[Astronuc]

We don't know m, and we can't get the F_F=(mu)F_N[/sup]

<sub>Chi meson was alluding to m*a = (mu) m*g => a = (mu) g and knowing a and g, one calculates 'mu'.


For the second problem, one string holds up the block. The vertical component of the Tension in the string at 50° supports the weight of the block. The horizontal component of the Tension in the string at 50° is balance by the Tension in the horizontal string.</sub>

 

[RoyalewithCh33s3]

Oh wow, I can't believe I didnt see that, I had it almost written like that except I dint have ma on the other side, in which case i would have no way to cancel the mass.

Thanks much both Chi and Astro!