topcat123
- 77
- 1
Homework Statement
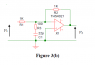
FIGURE 3(b) shows the THS4021 in a practical op-amp circuit with applied external compensation. Determine an expression for the low frequency gain of the circuit.
Homework Equations
The Attempt at a Solution
I really don't know where to start.
Is there a virtual Earth at the inverting input?