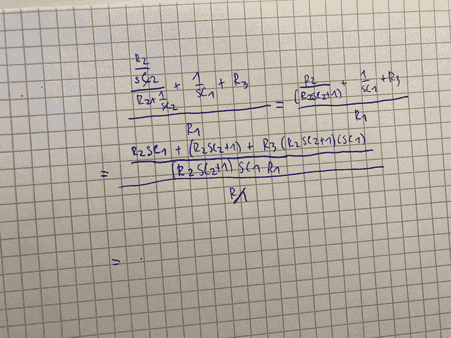SUMMARY
The discussion focuses on simplifying the output-to-input voltage ratio (Uout/Uin) in an operational amplifier (OPamp) circuit. The user successfully established the denominator in a factored form and is seeking guidance on simplifying the numerator, which involves expanding and collecting terms into a polynomial. The quadratic terms typically cannot be factored with real numbers, and the discussion emphasizes the importance of expressing these terms in a standard quadratic format, specifically as ({(s/ω0)}² + (s/Qω0) + 1). The conditions for real roots of the quadratic are also outlined, specifically that Q must be less than or equal to 1/2 for factorability.
PREREQUISITES
- Understanding of operational amplifier (OPamp) circuits
- Familiarity with voltage ratios and feedback mechanisms
- Knowledge of polynomial expressions and quadratic equations
- Basic concepts of resonant circuits and simple harmonic oscillators
NEXT STEPS
- Study the quadratic formula and its applications in circuit analysis
- Learn about the significance of the quality factor (Q) in resonant circuits
- Explore methods for analyzing OPamp frequency response
- Investigate techniques for polynomial factorization in electrical engineering
USEFUL FOR
Electrical engineers, circuit designers, and students studying operational amplifier circuits and their applications in signal processing.