oscar_lai_hk
- 12
- 0
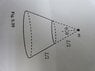
A mass is attached to one end of the massless string, the other and of which is attached to a foxed support. The mass swings around in a vertical circle as shown in Fig 5.36. Assuming that the mass has the minimum speed necessary at the top of the circle to keep the string from going slack, at what location should you cut the string so that the resulting projectile motion of the mass has its maximum height located directly above the center of the circle.