Parallel/Series circuit theory/concepts

[pugfug90]

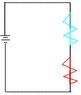
In my 1st pic.. would those be considered one, two, or no "branches"? Do branches only exist within parallel circuits?

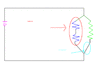
In my 2nd pic.. The dark blue "resistors"/"resistances" are one branch? And the diagonals separating the "resistors".. Are they simply wire (or medium)?

And what is a "junction"?
===
Summarized..
Am I correct in deducing that a "branch" only exists in a parallel circuit? And a branch is basically.. all of the "branches" of a parallel resistor.. And if there are resistors in series within a parallel resistor, you'd compound the series to form one resistor..

And.. what is the term for those jaggy things? Any difference between resistors and resistances? But you definitely don't call them circuits, right, since a circuit is the whole thing..

And what is a junction?

Thanks

 

[ranger]

For your first circuit, you can also say that all resistors are on the same branch so they have the same amount of current through them. You can think of a branch as a path way to a node.

For the 2nd circuit, the dark blue resistors are indeed on a branch by themselves. That "diagonal", is just a piece of wire.

And if there are resistors in series within a parallel resistor, you'd compound the series to form one resistor..

Yup, that's how you'd do it. Although I think you meant to say "series within a parallel branch."

And.. what is the term for those jaggy things? Any difference between resistors and resistances? But you definitely don't call them circuits, right, since a circuit is the whole thing..

Those "jaggy" things are resistors. Resistance is a property of resistors. Almost everything has resistance.

A junction is a point where two or more components connect.

 

[pugfug90]

Thanks :-)

"For your first circuit, you can also say that all resistors are on the same branch so they have the same amount of current through them. You can think of a branch as a path way to a node."

So if the red resistor was on the "south" part of the circuit while the blue one was still on the "east", would that still be 1 branch, or 2 branches?

"A junction is a point where two or more components connect."
That would be like in Diagram 2, where the two diagonals converge or diverge? Or in both, where the wire becomes perpendicular with another wire?

 

[ranger]

So if the red resistor was on the "south" part of the circuit while the blue one was still on the "east", would that still be 1 branch, or 2 branches?

It does note matter if the resistors were oriented north-south and east-west to each other. The important thing for this series circuit is that the same current will flow through them, therefore both of them must be on the same branch.

"A junction is a point where two or more components connect."
That would be like in Diagram 2, where the two diagonals converge or diverge? Or in both, where the wire becomes perpendicular with another wire?

Yup, that's correct. The ends or leads of the resistors meet at a point or connect, therefore it is a junction.
For the latter part of your question regarding the perpendicular situation. I'm not sure what exactly you are referring to. Could it be bottom and top of the both parallel branches? If so, it is a junction because multiple components connect at a given point.

 

[pugfug90]

On both of them, the general shape is a rectangle. Could I say that the corners of the rectangles are junctions?

 

[ranger]

Yes, you can say that for the two parallel branches, because at any corner, we have a lead from two resistors connecting.