Hi Orodruin, I forgot to ask another question (much simpler than before) regarding a different exam problem, and I thought I'd just write it here to save some time...
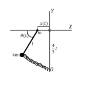
So when writing the kinetic energy for the Lagrangian ##( L = T - V )## of this system (diagram below), I got a little confused with whether I should use the centre of mass (## CM ##) for expressing the transnational component of the kinetic energy ##( T_t )##, or the 'point of suspension' (denote this by ## PoS ##) instead of the ## CM ##.
The reason I was confused was that clearly the rotational component of the kinetic energy ##( T_r )## was taken such that its rotational axis should be (into/ out of the page) at the point of suspension where the rod connects with the curved wire.
(i.e. I'd use the moment of inertia of the rod with the axis not at the ## CM ## but at one of the ends - which gives
$$ I = (1/3)ml^2 $$
rather than
$$ I = (1/12)ml^2 $$
the latter of which would be if the rotational axis was into the page, through the ## CM ## of the rod.
(using ##( T = T_t + T_r )## )
To put it in other words, should ## T_t ## be:
$$ T_t = (1/2)m( \mathbf {\dot r_{CM}} )^2 ...(1) $$
or should it be
$$ T_t = (1/2)m( \mathbf {\dot r_{PoS}} )^2 ...(2) ? $$
Whilst at the same time ## T_r ## has to be taken at the point of suspension regardless of what we do for transnational ## T_t ##:
i.e. $$ T_r = (1/2)I(\omega)^2 $$
where ## \omega = \dot { \theta} ## , with ## \theta ## being the angle between the rod and the vertical. And here ## I = (1/3)ml^2 ##. (Rotational axis being into the page through the point of suspension)
Also, the potential energy is purely gravitational, right?
Cheers