TheBC said:
Ghwellsjr, thanks for again putting so much effort in discussing diagrams.
You're welcome.
TheBC said:
ghwellsjr said:
I do not agree with you that the simultaneous green car events are 'really' 'physically' out there.
Then please tell me which events of the short green car are out there for Red between his red hands. (Definitely not the green rest car events!)
Just to make it clear, my issue with you is characterizing the
simultaneity of certain events as 'really' 'physically' out there.
But to answer your question: one of the events is labeled "A" in my three diagrams and the other one is labeled "C". In each diagram, the event labeled "A" is the same event. It has different coordinates in each diagram and once we know the coordinates in one diagram, the Lorentz Transformation process is how we determine what the coordinates for the same event are in another diagram. The event occurs 'really' and 'physically' out there when the "left" end of the green car becomes coincident with red's "left" fingertip. The coordinates that we apply to this event are totally arbitrary and do not have the attributes of 'really' or 'physically'.
Similar comments for event "C".
Thus, if it happens in a particular Inertial Reference Frame that they have the same time coordinate, then we say that they are simultaneous in that IRF. Events "A" and "C" have the same time coordinate in my first diagram and are therefore simultaneous in that IRF. In the other two IRFs depicted in the other two diagrams, events "A" and "C" have different time coordinates and are not simultaneous.
As far as I know, the foregoing is mainstream Special Relativity. I don't think it is just my opinion. If you don't accept it, then I don't think you are accepting mainstream Special Relativity.
TheBC said:
ghwellsjr said:
The simultaneity of the green car events are frame variant. Same with the red car events. Simultaneity is a coordinate effect.
I'm asking you:
which events of the short green train are between the red hands of the observer? The events of the green rest train? No. So, which events are between his hands? Please tell me.
In the second frame depicted in the second diagram, it is the same events labeled "A" and "C" which are also on the ends of the green rest train, or, as I prefer to say it, it is the frame in which the green train is at rest, or it is the green train's rest frame.
TheBC said:
I don't like at all you call it an 'effect'. The frame (any frame) indicates which events out of 4D spacetime existence form a 3D space of simultaneous event, i.o.w. the 3D world as it 'exists' at one moment in time.
You will tell me that that 3D world is 'arbitrarily 'chosen... I don't care less. Point is that an observer considers some events frome 4D spacetime as his 'real world now'. And because of relativity of simultaneity green's 3D world is different from red's 3D world.
I think the problem is that you consider an observer in a scenario to be locked into one particular frame, namely the frame in which he is at rest. I'm trying to point out that there is nothing that this observer can measure, observe or see that will force him to that conclusion. He must apply Einstein's simultaneity convention, which is what your red and green observers did in your scenario to arrive at the conclusion that what they felt on their fingertips occurred simultaneously. There's no dispute on that issue. What is in dispute is that Einstein's simultaneity convention is real and physical. In other words, two events are only simultaneous because we define them to be simultaneous. It is not a physical thing that we could let nature (the physical world) decide for us or that we could discover by only measurements or observations.
TheBC said:
The content of events is completely different. The only invariant in this exercise is the full picture: all the 4D spacetime events, the 4D spacetime world.
I don't know what you mean by this. What is the content of an event? The closest thing I can think of is its coordinates but you don't seem to be to appreciative of coordinates so I'm wondering if you mean that some events belong exclusively to a particular object and some other events belong exclusively to another (and some other events can belong to both objects). Is that what you mean, or something like that?
TheBC said:
ghwellsjr said:
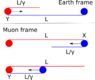
Only the first diagram is "as seen from the railway track".
I cannot see this. For me it's what red measures. In your first diagram I read that horizontally you give length12 for red car at rest and length 6 for short green car.
Yes, the grid lines going to the coordinate markings tell you that. Since the red car is at rest on the railway track and both are at rest in this IRF, we can say it is "as seen from the railway track". Those are your words. I would rather say that it is the mutual rest frame of the railway track and the red car because neither the railway track (or any observers stationed along it) nor the red car (or any observers stationed within it) can actually see most of the details that we can see when we look at the completed diagram. Of course, as I have repeatedly said, they can construct those details by sending and receiving radar signals and images from remote objects and applying Einstein's convention and doing a lot of calculations after the scenario is all done.
TheBC said:
ghwellsjr said:
Then I don't see why you would think a Loedel diagram is relevant for reciprocal length contraction.
Because Loedel shows you in one diagram the same proper rest length in both frames.
What is astonishing is that apparently you use your 3 rd diagram for other purposes that I would do. Because in no time I make it a loedel diagram. Your 3 rd diagram with coordinate distances is about a frame I am not interrested in. Because you don't show any of the 12 proper length or 6 long contracted cars in your 3 rd diagram. But the information is in your drawing, so why not showing it? Drop your irrelevant horizontal and vertical margins and read directly what red and green measure in their respective 3D space. Piece of cake. In next post I will mark up your diagram so it can be read as loedel.
I never said it was a Loedel diagram. I only provided the third diagram as a basis for making a Loedel diagram. Remember, I said that a Loedel diagram depicts three frames on the same diagram--all three of my diagrams get squeezed on to the one diagram by providing additional grid lines and markings--if you want to make it clear. As the wikipedia article says:
...there is a frame of reference between the resting and moving ones where their symmetry would be apparent. Such a frame of reference is a Loedel frame. In this frame, the two other frames are moving in opposite directions with equal speed.
Count them: there are three frames jammed into one diagram. I show all three frames as separate diagrams because it is so much easier to read and in this day of computers, they are so easy to generate. My problem with the Loedel diagram is providing the three sets of grid lines and three sets of markings. Since you leave them all out, I don't know how you can tell what is going on.
TheBC said:
ghwellsjr said:
Then I transformed the first chart to a speed of 57.7%c which is the speed at which both trains are traveling at the same speed.
I don't need this. Both cars are traveling relative to each other at same speed (0;866c). I don't need anything else.
I can easily see that each car is traveling at 57.7%c relative to the coordinates of the frame but how can you tell that each car is traveling at 0.866c relative to the other car?
TheBC said:
ghwellsjr said:
And why should you? Since both trains are traveling at the same speed, they are contracted to the same length. There's nothing sacrosanct about the length of 6 feet. You only get a contraction to 50% of the Proper Length of 12 feet when the speed is 86.6%c. Since these trains are traveling at 57.7%c, they are contracted to 1/1.22 or just under 10 feet as the diagram shows.
I don't need the 57.7%c. Once more: it's about reciprocal length contraction between the 2 cars. They are traveling at 86.6%c relative to each other. And that's all I need.
Your first diagram shows red's frame: a 12 long red car for red observer and a 6 long green car.
Your second chart shows green's frame: 12 long green car for green observer and a 6 long red car.
Your 3 rd diagram is a loedel diagram only if you also indicate the green and red frames in which you read proper and contracted lengths on both axes with one and same ruler.
I agree, if you transformed the grid lines for the first two diagrams so that you could actually indicate the 12-foot Proper Length of each car and the 6-foot Contracted Length from the other car's rest frame but instead, you have a magic ruler. How do you "calibrate" this ruler? How do you know how to lay it on the diagram to get the measurements. Do the red and green observers have access to this ruler?
TheBC said:
ghwellsjr said:
That's because you are adding the coordinates from two other frames to the original frame. Nothing wrong with that, as long as your audience understands how to read the diagram. If the two added sets of coordinates are not drawn on the diagram, then it becomes very difficult to understand how to read it.
I never said is is 'easy' to read. But let's be honnest; do you find a Minkoski diagram, with different unit lengths for time and space 'easy' to read reciprocal length contraction and time dilation? Forget it.
No, I don't find the typical Minkowski diagram, with or without grids and markings easy to read. But I understand their historical significance--and Loedel diagrams--because it was fairly difficult to make any diagram by hand but with our computers, it is easy to make interactive diagrams where the user can "dial" in any speed he wants to see how the Lorentz Transformation process creates additional IRF's.
TheBC said:
I find loedel A LOT easier to read than your or Minkowski... But it has it's limitations. More than 2 frames f.ex. Because then not all frames keep same unit lenghts...
But for most exercises where only two relative moving systems are used loedel is sublime.
That's only one exercise. Two inertial observers. It can't even show the most popular of all scenarios, the Twin Paradox. My diagrams are trivially easy to read (as you have already demonstrated) and can be used with any in-line scenario. And I can even expand to non-inertial frames using the exact same techniques that observers can use to construct Inertial Reference Frames. They are truly sublime.
But I don't object to a properly drawn and marked Loedel diagram with enough explanation to make its interpretation clear. I do object to the idea that it conveys anything more than any other properly drawn diagram.
TheBC said:
ghwellsjr said:
I just prefer separate clearly marked diagrams.
This is where we disagree. Dalespam too does not see any advantage of one loedel over 2 separate diagrams because it does not show more raw date than your two diagrams. In that sense raw data written on a piece of paper, cut to pieces and thrown on the floor also 'contains' all the information. But Loedel shows clearly how all rest and shorter 'moving' length are part of one full 4D spacetime diagram. With one ruler.
Again, you are giving preference to each observer's rest frame and concluding that both are in operation at the same time and ignoring the fact that any other frame is just as valid.
TheBC said:
ghwellsjr said:
But you can easily calculate it using the formula for the spacetime interval.
There we are. With loedel you do not have to calculate it. You just measure it all with one and the same ruler. And believe it or not, it's on your diagram but apparently you are not aware of it.
I'm not aware of where you got the 12-foot length of the ruler that you can place in just the right spot to measure both the Proper Length of one car and the Contracted Length of the other car. How do you determine that it's 12 feet long and not 8? Where do you get the information from that it is 12? And how do you know what angle to draw the two sets of lines at? And where do you show the relative speed between the two observers?
TheBC said:
ghwellsjr said:
As I see it, the Proper Length between A and C is the distance between red's fingertips (6 feet) in the first diagram. I don't know where you got the 12 from.
(In first diagram) Then what represents the distance between your two vertical red lines of the red car (at rest for red)?
If you're asking about the two outside vertical red lines, then, yes, they are 12 feet apart, but you were not talking about those two lines, you were talking about the proper red length between A and C, which is 6 feet. Here's what you said:
TheBC said:
the proper red length (12) between A and C; i.e. the line (not drawn in your IRF charts but essential in Loedel -and SR!) between A and C because that line is the collection of events the shorter train is made of. Same remark for proper green length between E and G (12).
TheBC said:
ghwellsjr said:
And E-G is the proper length between green's fingertips, not the green train in the second diagram.
Correct. Sorry about that. My mistake.
And you made the same mistake regarding A-C, correct?
TheBC said:
ghwellsjr said:
I thought I did what you wanted. Did you see the line segments A-D-C and E-H-G? Maybe you're looking at it on a small screen.
I saw them full scale, but they are not what I asked.
Once more: quote<<Draw on the diagram the light paths from the rear and front of the
green rest train and see where they end at
red's head. That's a complete different story, irrelevant for red's measurement of a shorter green train.>>
Now this one is my mistake. I didn't do what you asked but here it is now:
But I still don't understand why you want this drawing, please explain.
TheBC said:
In fact you should draw a line between E-G en continue to the green worldlines of the front and rear of green car. The line is 'made of'/represents all the events that are simultaneous for green at one moment of time on green's wristwatch.
Similar reasoning for red. That red line is 'made of'/represents all the events that are simultanoeus for red.
The second diagram already has a grid line corresponding to simultaneous events that include events E and G and the first diagram has a grid line corresponding to simultaneous events that include A and C.
TheBC said:
I'll let him comment if he wants to.