Perspective on Relativity and Length Contraction

[Dale]

A Loedel diagram works the exact same way that any spacetime diagram works. All it is is a standard spacetime diagram from the "halfway" frame with the two moving frame's axes drawn and the "halfway" frame's axes suppressed. You are not missing anything, ghwellsjr.

You calibrate your ruler by the usual Lorentz factor in the "halfway" frame. You find the relative speed by looking at each moving frame's coordinates, although that is rather difficult to do. By events belonging to an object he just means that those events are on the world-tube of the respective object.

I prefer your clean diagrams. Less (clutter) is more (informative).

 

[ghwellsjr]

I wonder what people think of the following scenario (unfortunately not feasible, in practice):


Imagine two space beacons at mutual rest, separated by e.g. a million kilometers. A rocket passes them, turns, passes them again, turns, etc. On each passage the speed of the rocket relative to the beacons increases. The rocket can directly measure (theoretically) the relative speed of a beacon by measuring the time it takes to traverse the length of the rocket. The rocket can also measure the time it takes for both beacons to pass. [All acceleration occurs during the turnarounds, so no proper acceleration is measured in the rocket while the beacons are passing.]

On the first, slow, crossing the rocket measures D as the beacon separation by computing v (measured locally as described above) multiplied by the crossing time. However, following the identical procedure each time to measure v, and crossing time, D will be found to get smaller and smaller as v increases closer to c on each passing.

Note that since v is measured locally by the rocket on each passing, using its own clock, time dilation plays no role in this (at least for the rocket).

1) Do any of the participants believe that if the enormous engineering problems could be solved, that the observed result would be different from what is described above?

2) If not, is there any explanatory model other than distance contraction (at least for the rocket)?

All measurements are local measurements in a rocket inertial frame. We measure speed of a passing beacon, and time between one passing and then the other. One pair of local clocks, one ruler, all on/in rocket are all that are used.

I would like to draw some spacetime diagrams to depict what I think you are proposing. However, I prefer to work with feet rather than meters so that I can use the speed of light as 1 foot per nanosecond or 1 billion feet per second. I set the distance between the beacons in their mutual rest frame at 3 billion feet which is just a little shorter than a million kilometers. (I'm using the American definition of billion here, 10⁹.) I'm also using a very long rocket, 1 billion feet, just so that it will show up clearly on the diagrams but it won't make any difference to the principles illustrated.

I start with the mutual rest frame of the two beacons in green and red and the rocket with its front end in black and its rear end in blue approaching from the left at 0.6c. The dots on the rocket's worldlines mark off 1-second increments of Proper Time on the two clocks that you mentioned:

Now I transform to the rest frame of the rocket where we see that its length is 1 billion feet and its two clocks have been synchronized and correspond to the Coordinate Time:

Correct me if I'm wrong but I believe you described the rocket's measurement of the distance between the two beacons starting with it determining the speed of at least one of the beacons. It does this by noting its time on the black clock (0 secs) when the beacon passes it. Then it observes the time on the blue clock (1.667 secs) when the beacon reaches the rear of the rocket. Since its ruler (basically the rocket itself) sets the distance between these two measurements at 1 billion feet, it determines the speed of the beacon to be 1 billion feet divided by 1.667 seconds or 0.6 billion feet per second which is the correct answer of 0.6c.

Next the rocket measures the time that the second red beacon passes it (4 seconds) and determines that the distance between the two beacons is d=vt or 0.6 billion feet per second times 4 seconds which equals 2.4 billion feet, the correct length-contracted answer.

I want to emphasize the point that although we show these measurements being made in the rocket's rest frame, it doesn't matter which frame we use to describe the scenario. For example, you can go back to the first diagram, the mutual rest frame of the beacons and the exact same measurements and observations and determinations are made.

The particular scenario that I presented was in the middle of the iterative process that you described: in particular, the rocket has made many crossings, accelerating and reversing direction after each one so that each successive crossing is made at a higher speed. However, there are two problems with the scenario as described. The first is that the two clocks will not remain in sync after the rocket has accelerated and so they will have to be re-synced. The second is that there is no guarantee that the length of the rocket (or ruler) will remain the same Proper Length after it undergoes the acceleration. We can solve both of these problems by using the radar method to re-sync the remote clock and re-calibrate the length of the rocket. Here is a spacetime diagram to show how this is done using the same speeds and distances as the first set. You can assume that the clocks begin out of sync (as shown in the diagram) and the exact rocket length is unknown because this scenario is just one in a long line of iterations:

Some time after the turn-around acceleration when all the stresses have dampened out but before the rocket has reached the first beacon, the captain at the black front end of the rocket (at his time of -3 secs) sends a radar signal to the blue rear end of the rocket (shown as the bottom thin black line) which either passively reflects the signal back or actively regenerates a return signal (instantly) which the captain receives at his time of -1 secs (shown as the thin blue line). He then applies Einstein's synchronization convention (his second postulate) and assumes that the time it took for the radar signal to get to the rear of the rocket is equal to the time it took for the return to get back to him. He takes the half-way point of the interval (-2 secs) and assumes that the radar signal arrived at the rear at that time. But now he also knows that it will take another second for a message that he sends at his time of -1 secs to get to the rear of the rocket which means that his own clock will then be at 0 secs. So he tells the operator at the rear of the rocket (or has automatic equipment to do this) to set his clock to 0 secs when he receives the message.

Furthermore, since the roundtrip time for the radar signal to get to and from the rear of the rocket was 2 seconds, the captain assumes that the length of the rocket is one-half the distance that light travels during that interval or 1 light-second or 1 billion feet.

Now the captain can pick up his measurements as he did before. I go through this explanation because the captain will have to perform it again after each acceleration and change of direction before the next crossing.

Next I want to show how the same process works in the mutual rest frame of the beacons:

Note that the captain's assumption that the signal takes the same amount of time to get to the rear of the rocket as it does to return is not correct in this frame but it doesn't matter. And the determination of the length of the rocket is not correct. Neither is the calculation of the speed of the beacons or their distance apart. Everything's wrong except that this frame correctly shows exactly the same measurements and observations as was determined in the rocket's rest frame where everything was correct. This is to again emphasize the point that the frame that we are depicting the scenario in has no bearing on the measurements, observations, assumptions and determinations for the captain.

But now I want to show that there is an even simpler way for the captain to make his determination of the distance between the beacons and yet it involves the same process of radar signals but doesn't require a ruler or a second clock or the need to synchronize or re-calibrate them.

In this process, the captain makes successive radar measurements of the distance to one of the beacons and from this he can determine its speed. He can do this before the beacon gets close to him or after it passes him. I will take advantage of one of those measurements when the beacon passes the captain and the distance is zero. Some arbitrary time later, I use one second simply because it is convenient, he sends out a radar signal which returns to him at his time of 4 seconds. From this he determines that at his time of 2.5 seconds (half-way between sending and receiving) the beacon was 1.5 light-seconds or 1.5 billion feet away. From these he determines its speed to be 1.5/2.5 or 0.6c, just like before. And he determines the distance between the beacons just like before as 0.6 times 4 or 2.4 billion feet:

Finally, I show this last process in the mutual rest frame of the beacons:

Again, all measurements are the same.

 

[ghwellsjr]

Now as if things didn't get simple enough, we can make them even simpler. It is not necessary for the captain to first determine the speed of the beacons in order to calculate their separation. He can do it directly with radar signals. Of course, he can't know ahead of time when to send out the radar signals so we imagine that he is doing it continuously but I'm only going to show the important ones. He would send out one set of signals to the green beacon and a second set to the red beacon and by matching the times determined by the reflections, he can determine the distance between the beacons.

To start with, though, I'm going to take advantage of the fact that he is colocated with one of the beacons at a particular time and so he only has to measure the distance to the other beacon. Here is the diagram for that situation:

A few seconds after he has passed the green beacon, he looks at his log of sent/received radar times for the red beacon and finds one that determines a measurement taken at the same time he was colocated with the green beacon, his time of zero seconds and that is the one that I show in the above diagram. He notes that he sent that radar signal at his time of -2.4 secs and received the return signal at 2.4 secs which allows him to determine that the red beacon was 2.4 light-seconds or 2.4 billion feet away.

Here is how it looks in the rest frame of the beacons:

If the captain is keeping track of the speed versus Length Contraction for the different iterations, he can calculate the speed as 2.4 light-seconds divided by 4 seconds or 0.6c.

He looks in his log and finds another set corresponding to this diagram:

The two radar signals above were sent in opposite directions at his time of 0.8 secs and received at his time of 3.2 secs. Since these obviously calculate to the same time, the distance in each direction is simply (3.2-0.8)/2=2.4/2=1.2 billion feet or a total of 2.4 billion feet.

Here's how this one looks in the beacons' rest frame:

The captain continues to look in his log and finds one corresponding to this diagram:

In this one, the signals to the two beacons were sent in the same direction (behind him). The one to the green beacon was sent at 2 secs and the return received at 8 seconds. One half of the difference is 3 seconds corresponding to a distance of 3 light-seconds or 3 billion feet and the time is the average or 5 seconds. The signal to the red beacon was sent at 4.4 secs and its return arrived at 5.6 secs. One half of the difference is 0.6 seconds corresponding to a distance of 0.6 billion feet at a time of 5 seconds. The difference between the two distance measurements is 3-0.6 or 2.4 billion feet.

Finally, the same scenario in the rest frame of the beacons:

 

[PAllen]

I would like to draw some spacetime diagrams to depict what I think you are proposing. However, I prefer to work with feet rather than meters so that I can use the speed of light as 1 foot per nanosecond or 1 billion feet per second. I set the distance between the beacons in their mutual rest frame at 3 billion feet which is just a little shorter than a million kilometers. (I'm using the American definition of billion here, 10⁹.) I'm also using a very long rocket, 1 billion feet, just so that it will show up clearly on the diagrams but it won't make any difference to the principles illustrated.

...

Thanks a lot for these and the following series of illustrations. Indeed, you have understood my scenario perfectly.

However, I want to discuss two points you raise and also motivate the seeming complexity of what I proposed.

My first goal was to verify whether or not universal_101 (in obsessing over the idea that length contraction has not been 'directly' observed) believed that an attempt to do so would come out differently than SR predicts. For this purpose, I wanted an in principle experiment which would be hard to understand as anything other than length contraction and also one that used only procedures valid both for Newtonian mechanics and SR. It would thus, if achieved, select SR, via observed length contraction, using no assumptions that distinguish SR from Newtonian mechanics (e.g. invariant two way lightspeed, which is false both in Newtonian corpuscular theory or pre-SR aether theory).

As you note, I glossed over the issues of synchronizing the clocks in front and back of the rocket, and also the constancy of the length of the rocket. I will now un-gloss over those issues, showing how they could be addressed exactly, in principle, in the meta-theory encompassing Newtonian physics and SR. The key features of the meta-theory are the POR and homogeneity and isotropy.

First, as to ship length, all we need assume is that prior to constructing the rocket we have found ideally rigid materials, with rigidity so defined as to be perfectly consistent with SR as well as Newtonian physics. A simple approach is that the material however, stressed, when unstressed and allowed time for relaxation, exactly retains all of its dimensions (as long as it doesn't break). There is no classical theoretical lower limit to coefficient of thermal expansion, so we can propose a value of zero for our ideal material. This definition of rigidity is perfectly consistent with both SR and Newtonian physics and removes the need to re-measure the rocked after turnarounds - we just need to allow for time for relaxation (and SR does provide a precise lower bound on the minimum time for this).

Second, as to the clocks, we need a procedure to ensure they remain in synch that is exactly valid both for Newtonian physics and SR. This means we can not use either slow clock transport (exactly valid in SR only in a theoretical limit of infinite time), nor light signals (because we don't want to assume SR). The key hint is isotropy and homogeneity. We move two perfect clocks to the center of the rocket and synchronize them. When we want to make an inertial measurement with the clocks separated, we move them with identical motion profiles to opposite ends of the rocket. As this is done while the rocket is inertial, these two clocks remain exactly synchronized with respect to each other, in both SR and Newtonian physics (in SR, they would no longer be in synch with a clock that remained at the center, but we don't care about this). This procedure is relying on homogeneity and isotropy guaranteeing that the result is the same as long as the motions are symmetric. Then, before any acceleration of the rocket, we move the clocks back to the center, again with exactly symmetric motion.

 

[nitsuj]

My first goal was to verify whether or not universal_101 (in obsessing over the idea that length contraction has not been 'directly' observed) believed that an attempt to do so would come out differently than SR predicts. For this purpose, I wanted an in principle experiment which would be hard to understand as anything other than length contraction and also one that used only procedures valid both for Newtonian mechanics and SR.

Has time dilation from relative velocity been "directly" observed in a more "direct" way then length contraction? I don't think so.

Differential aging from relative motion is as much a result of time dilation as it is length contraction, specifically the invariance of c.

imo this seems to be more about hammering out a definition of "directly" observed, and in the context of variant measurements

 

[PAllen]

Has time dilation from relative velocity been "directly" observed in a more "direct" way then length contraction? I don't think so.

Differential aging from relative motion is as much a result of time dilation as it is length contraction, specifically the invariance of c.

imo this seems to be more about hammering out a definition of "directly" observed, and in the context of variant measurements

Muon's reaching the ground is accepted (even by skeptics in this thread) as a direct measure of time dilation in the Earth frame (not twin differential aging). In the muon frame it would be an observation of length contraction, but 'we' are not in the muon frame. In my scenario, my rocket frames (for each inertial velocity) create a family of 'muon frames' in relation to the beacons, with a direct way of measuring a long length - and finding it getting shorter and shorter.

 

[nitsuj]

Muon's reaching the ground is accepted (even by skeptics in this thread) as a direct measure of time dilation in the Earth frame (not twin differential aging).

That's what I'm finding so bizarre is that is accepted as a "direct" measure of time dilation, but not length contraction, surely those "skeptics" agree the muons measure proper time. Also, I'd consider the "landing" of the muon the comparative of proper times and noting differential aging. However I don't see any "direct" measure of time dilation.

In the muon frame it would be an observation of length contraction, but 'we' are not in the muon frame. In my scenario, my rocket frames (for each inertial velocity) create a family of 'muon frames' in relation to the beacons, with a direct way of measuring a long length - and finding it getting shorter and shorter.

A neat way to illustrate it for sure!

 

[PAllen]

That's what I'm finding so bizarre is that is accepted as a "direct" measure of time dilation, but not length contraction, surely those "skeptics" agree the muons measure proper time. Also, I'd consider the "landing" of the muon the comparative of proper times and noting differential aging. However I don't see any "direct" measure of time dilation.

Differential aging refers to two clocks that start and end coincident. The result is that the ensuing discrepancy in their measured times is not only invariant, but that the explanation is time dilation in alll reference frames. Sometimes forgotten is that where the time difference emerges along the world lines is frame dependent, so the idea of a frame dependent explanation is in common with the muon case (except that it always involves time dilation).

The muon case is definitely not a case of differential aging. There are no two clocks that separate and come together. In one frame you have pure time dilation (not differential aging). In another frame you have pure length contraction - no time dilation at all involved in the explanation.

 

[nitsuj]

The muon case is definitely not a case of differential aging. There are no two clocks that separate and come together. In one frame you have pure time dilation (not differential aging). In another frame you have pure length contraction - no time dilation at all involved in the explanation.

Ah i See

 

[bobc2]

Excellent 4-D Pictures

Ghwellsjr,
I quickly transformed your 3rd diagram into a full Loedel diagram, with lots of dots representing the events of 4D spacetime existence of red and green car. Please take the time to scrutinize this sketch before it is considered clutter and deleted from the thread... ;-)

TheBC, I've appreciated your many efforts at explaining Special Relativity with your Loedel space-time diagrams. Good work! It saddens me to see the response you get on the forum. Particularly when your sketches are passed off as meaningless, since they are merely coordinate representations -- as though coordinate representations have no relevance to reality. That's like telling your physics instructor in a General Physics class that his picture of the trajectory of a cannon ball has no relevance to reality because it is merely a coordinate representation. And it is a pity that your work is dismissed because it's too complicated for some to comprehend.

Your coordinate representations are right on target. You would have been a marked student in my University physics class when I taught Loedel diagrams as part of the section on Special Relativity. (my students didn't seem to find it nearly so difficult a concept as those riling against you here). I'm confident I would be grading you with an A+.

 

[Mentz114]

And it is a pity that your work is dismissed because it's too complicated for some to comprehend.

Your coordinate representations are right on target. You would have been a marked student in my University physics class when I taught Loedel diagrams as part of the section on Special Relativity. (my students didn't seem to find it nearly so difficult a concept as those riling against you here). I'm confident I would be grading you with an A+.

I think most posters here understand what the Loedel diagram means. But it picks two inertial frames and shows only those. The regular Minkowski diagram can be transformed to show the POV of any set of inertial frames.

I suggest that insisting that the Loedel diagram is better in some way is just prejudice on your part. Insulting people who don't agree with you is just offensive and unnecessary.

 

[bobc2]

TheBC Loedel Diagrams

I think most posters here understand what the Loedel diagram means. But it picks two inertial frames and shows only those. The regular Minkowski diagram can be transformed to show the POV of any set of inertial frames.

I hope you are not implying that the choice of which pair of observers is limited. Of course that is not the case. Any two observers in motion with constant velocity with respect to each other may be selected for a Loedel-Minkowski diagram. And there has been no claim that the Loedel-Minkowski diagram is always the preferred method of presenting the concept. The standard Minkowski diagram together with the Loedel-Minkowski representation is usually quite useful.

The Loedel-Minkowski picture is particularly applicable to the subject of this thread. My comments were not meant as an insult to anyone but rather as a compliment and encouragement to TheBC for his excellent presentations and persistence under hostile posts.

 

[ghwellsjr]

Ghwellsjr,
I quickly transformed your 3rd diagram into a full Loedel diagram, with lots of dots representing the events of 4D spacetime existence of red and green car. Please take the time to scrutinize this sketch before it is considered clutter and deleted from the thread... ;-)

TheBC, I've appreciated your many efforts at explaining Special Relativity with your Loedel space-time diagrams. Good work! It saddens me to see the response you get on the forum. Particularly when your sketches are passed off as meaningless, since they are merely coordinate representations -- as though coordinate representations have no relevance to reality. That's like telling your physics instructor in a General Physics class that his picture of the trajectory of a cannon ball has no relevance to reality because it is merely a coordinate representation. And it is a pity that your work is dismissed because it's too complicated for some to comprehend.

Your coordinate representations are right on target.

I didn't think TheBC agreed that Length Contraction was simply a coordinate effect:

O.K. guys, this is getting out of hand. It's really too ridiculous to waste more time on this.
I'll get back to this forum the day you know what events are, how loedel works, and what SR is about.
Untill then; good luck with your coordinate effects.

You would have been a marked student in my University physics class when I taught Loedel diagrams as part of the section on Special Relativity. (my students didn't seem to find it nearly so difficult a concept as those riling against you here). I'm confident I would be grading you with an A+.

Since you have been a teacher of Loedel diagrams then maybe you can answer my simple questions to TheBC from post #148:

How did you determine the values of 12 and 6? Where did you get this ruler from that has those markings?

Where do you see on this diagram that the two observers are traveling at 0.866c relative to each other?

 

[Mentz114]

My comments were not meant as an insult to anyone but rather as a compliment and encouragement to TheBC for his excellent presentations and persistence under hostile posts.

Sure. I suppose that if 'complicated' is taken as meaning 'clutterful' then it is too complicated. But never in the other possible sense of complicated.

 

[jartsa]

How so? I don't get what you think the problem is.

Regarding reciprocal, in the Earth's frame the muon is contracted, in the muon's frame the Earth is contracted. Again, no problem. Just apply the Lorentz transform from one frame to get the other. No problem.

A fast muon thinks the distance to Earth is contracted and short.

Earth thinks the distance to the same muon is contracted and long.

Well, Earth should think that way IMHO. It should think: "Just by going into a different frame I can make the distance longer, the uncontracted distance is the longest of the distances in different frames."


Is it possible for the earh to make the distance longer?
Well, it's possible for the muon, so reciprocally it should be possible for the earth.

 

[Dale]

Earth thinks the distance to the same muon is contracted and long.

The distance to the muon is changing over time, so the length contraction formula doesn't even apply. You cannot use a formula in a circumstance which violates one of the assumptions used in the derivation of the formula. The distance between the Earth and the muon requires the full Lorentz transform, not just the simplified length contraction formula.

The distance between the top of the atmosphere (muon source) and the bottom of the atmosphere (muon detector) is not changing over time, so the length contraction formula applies. That distance is uncontracted in the Earth's frame and contracted in the muons frame.

 

[nitsuj]

Differential aging refers to two clocks that start and end coincident.

I've searched a fair bit for any definition for Differential aging and haven't found anything. Where did yours come from? Can you direct me to a source?

Also it reads as though muon decay is very consistent...like a clock, and is the point to them being reliable for such experiments. If muons decay at the same rate, the lifetime taken in a lab compared to the life time of those atmosphere ones seems to circumnavigate that before 'n after clock comparison requirement for differential aging that you mentioned.

So I guess I don't see your perspective, less the "we are not in the muons frame see we don't measure length contraction." Though the muon it self is length contracted in the "at home" frame so with magical idealized measurements I suppose it could be "directly" measured.

Here is wikis definition for time dilation;
"In the theory of relativity, time dilation is an actual difference of elapsed time between two events as measured by observers..."

What is the elapsed time the muon measures? rhetorical.

 

[PAllen]

I've searched a fair bit for any definition for Differential aging and haven't found anything. Where did yours come from? Can you direct me to a source?

Also it reads as though muon decay is very consistent...like a clock, and is the point to them being reliable for such experiments. If muons decay at the same rate, the lifetime taken in a lab compared to the life time of those atmosphere ones seems to circumnavigate that before 'n after clock comparison requirement for differential aging that you mentioned.

So I guess I don't see your perspective, less the "we are not in the muons frame see we don't measure length contraction." Though the muon it self is length contracted in the "at home" frame so with magical idealized measurements I suppose it could be "directly" measured.

Here is wikis definition for time dilation;
"In the theory of relativity, time dilation is an actual difference of elapsed time between two events as measured by observers..."

What is the elapsed time the muon measures? rhetorical.

Differential aging is the more technical term for twin paradox scenario. The fundamental feature is that both twins (clocks) agree which one elapsed more time. The defining feature is two clocks starting and ending together, thus two space time paths between one pair of events.

Time dilation is frame or coordinate dependent and, in SR, is symmetric. The muon considers Earth clocks to be slow; the Earth considers the muon clock (decay rate to be slow). Time dilation is defined as the ratio between the rate on some clock moving in some coordinate system and the time measured in that coordinate system. It can be defined for one world line expressed in some coordinates. Indeed, there is only one world line of interest between the muon creation and detection - the muon world line. There is no other clock that follows a different path between the creation and detection event.

This single muon world line elapses much less than two microseconds proper time, in all frames. In the muon frame, there is not time dilation at all - the ratio of proper time to coordinate time is 1. Instead, the explanation of why it reaches the ground is that the ground is very close at the time (per the muon) that the muon is created. Also, in this frame, the ratio of Earth clock rate to muon coordinate time is <<1, but this has no bearing on why the ground reaches the muon.

For earth, the ground and muon are far apart at the time (per earth) of muon creation. The muon reaches the ground by virtue of time dilation: the ratio of proper time on the muon world line to Earth coordinate time is <<1. Also, if two muons created in succession are 1 meter apart as they measure it (assuming they are co-moving, thus mutually stationary), they are <<1 meter apart per Earth coordinates - but this has no relevance to why they reach the ground, using Earth coordinates.

 

[ghwellsjr]

Time dilation is defined as the ratio between the rate on some clock moving in some coordinate system and the time measured in that coordinate system.

Although we often refer to the rate of a clock, it's actually the period of a time interval on a clock that we are concerned with since Time Dilation means something is stretched out--gotten bigger (the opposite of Length Contraction). Seconds last longer on a moving clock compared to the seconds of the coordinate system. So the precise definition of Time Dilation is the ratio of the Coordinate Time to the Proper Time of a clock moving according to the coordinate frame. Thus the Time Dilation factor is always a number greater than 1. It's equal to the Lorentz Factor known as gamma.

 

[ghwellsjr]

A fast muon thinks the distance to Earth is contracted and short.

Earth thinks the distance to the same muon is contracted and long.

Well, Earth should think that way IMHO. It should think: "Just by going into a different frame I can make the distance longer, the uncontracted distance is the longest of the distances in different frames."


Is it possible for the earh to make the distance longer?
Well, it's possible for the muon, so reciprocally it should be possible for the earth.

You can only appeal to reciprocity when the scenario is reciprocal (and symmetrical). We can change the scenario to one that is reciprocal and then we can apply Length Contraction equally.

So let's consider a spaceship that is 1000 feet long approaching the Earth at a speed of -99%c and we'll look at what happens as it reaches a point in the sky that is 1000 feet above the surface of the earth.

I'm going to draw some spacetime diagrams that are a little unusual in the sense that they have distance along the vertical axis and time along the horizontal axis. I think this will make it clearer in thinking about the spaceship coming straight down towards the Earth (or the Earth coming up straight towards the spaceship).

The surface of the Earth is shown as a green line with the point in the sky at 1000 feet in blue. The front end of the spaceship is shown as a black line and the rear in red. To begin with, I put the origin of the diagram at the point of contact between the black front of the spaceship and the blue point in the sky. That is why the surface of the Earth is at -1000 feet in the first diagram. The dots represent 1-microsecond intervals of time covering a range of just 2 microseconds. The speed of light is 1000 feet per microsecond.

Here's the first diagram showing the rest frame of the earth/sky:

Now I transform the coordinates of the first diagram to a frame moving at -99%c which is the rest frame of the spaceship:

If you compare these two diagrams, you will see that they are exactly reciprocal. The Lorentz Factor at 99%c is just over 7 so the time for the moving object is dilated meaning that 2 usecs of its Proper Time takes 14 usecs of Coordinate Time and the 1000-foot distance for the "objects" is Length Contracted from 1000 feet to 141 feet. Note also that because of the Relativity of Simultaneity, the Proper Time at one end of the object is offset from the other end of the object.

But to get closer to the situation for a muon, we need to use a shorter length for the spaceship. A muon is actually a very small fraction of a foot but I'm just going to shorten the length from 1000 feet to 100 feet so that you can see the trend:

Note now that the offset between the front and rear of the spaceship is one seventh of what it used to be and the distance between the black and red lines is not even visible on the diagram. I think you can see that if we went a million times smaller, there would be no practical difference between the black and the red lines. So this represents the first point of departure from a reciprocal scenario to one that is not reciprocal.

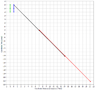
Next, we want to make several changes in the relationship between the surface of the Earth and the point in the sky. First, we want to make the point of contact (the origin) be the surface of the Earth and not someplace up in the sky. In fact we want to consider the point in the sky as being analogous to the creation of the muon and so it must occur much earlier so we need to extend the timeline of the earth/sky to 15 microseconds instead of only 2 microseconds. Here's the spacetime diagram for the final scenario:

Note that in the above diagram, the time for the Earth is the same as the Coordinate Time and the time when the spaceship arrives at the 14000-foot altitude above Earth is just over 14 microseconds before the time of impact with the surface of the earth. Note also that time for the spaceship is dilated so that 2 seconds on its clock is stretched out to just over 14 microseconds of Coordinate Time during its trip. Finally, note that the length of the spaceship has been contracted so that instead of 100 feet (which would be noticeable on the diagram) it is only 14 feet (which is not noticeable).

Now we want to see what this scenario looks like when we transform to the rest frame of the spaceship. I have to change the scale of the coordinates so that it will fit on the page:

Unfortunately, we lose all the important details so I'll zoom back into the same scale I had before and focus on the activity of the spaceship:

Now we can see that the time for the Earth and sky is dilated so that each microsecond of their Proper Time is stretched out to just over 7 microseconds of Coordinate Time. We can also see the Proper Length of the spaceship at 100 feet but the distance between the sky and the Earth is contracted from 14,000 feet to about 2000 feet.

So as you can see, Time Dilation and Length Contraction still apply to both the earth/sky frame and the spaceship frame, it's just that the Earth doesn't care about how the spaceship is Length Contracted (and especially for a muon that is billions of times smaller than a spaceship), the Earth only cares about the Time Dilation of the spaceship (or muon) so that it can survive a 14,000 foot trip at 99%c in only 2 microseconds of its time. Without Time Dilation, it would not even be able to get down to the 12,000-foot altitude.

And the spaceship (or muon) doesn't care about how time for the earth/sky is dilated (even though it is), it only cares about the Length Contraction of the distance between the sky at 14,000 feet and the surface of the Earth (at zero feet) which is contracted to about 2000 feet. So instead of the Earth starting out at 14,000 feet below it, it starts out at only 2000 feet below it and coming up at 99%c so that it only takes 2 microseconds of its own time for the Earth to reach the spaceship (or muon).

So the bottom line is that since the final scenario is not symmetrical and reciprocal, the details of how we apply both Time Dilation and Length Contraction are not the same in both frames like they were in the first symmetrical scenario.

Does that make it all perfectly clear? Any Questions?

 

[ghwellsjr]

For those that would like to see the spacetime diagrams in the previous post in the normal format, here are thumbnails for them:

 

[PAllen]

Although we often refer to the rate of a clock, it's actually the period of a time interval on a clock that we are concerned with since Time Dilation means something is stretched out--gotten bigger (the opposite of Length Contraction). Seconds last longer on a moving clock compared to the seconds of the coordinate system. So the precise definition of Time Dilation is the ratio of the Coordinate Time to the Proper Time of a clock moving according to the coordinate frame. Thus the Time Dilation factor is always a number greater than 1. It's equal to the Lorentz Factor known as gamma.

I agree this is the standard definition for time dilation factor. However, I did not actually use that term. I spoke of rate of time on clock to coordinate time being << 1, which is correct, and is time dilation.

 

[ghwellsjr]

I agree this is the standard definition for time dilation factor. However, I did not actually use that term. I spoke of rate of time on clock to coordinate time being << 1, which is correct, and is time dilation.

Are you saying that there is a difference between the terms "time dilation factor" and "time dilation" (without the word "factor")? And that even though "dilation" means "expansion" or "enlargement", we can use the term in the sense of "contraction" or "reduction" if we leave off the word "factor"?

 

[DrGreg]

Are you saying that there is a difference between the terms "time dilation factor" and "time dilation" (without the word "factor")? And that even though "dilation" means "expansion" or "enlargement", we can use the term in the sense of "contraction" or "reduction" if we leave off the word "factor"?

"Time" and "rate" are reciprocals of each other, so "rate contraction" means the same as "time dilation". But no-one ever uses the phrase "rate contraction".

 

[PAllen]

Are you saying that there is a difference between the terms "time dilation factor" and "time dilation" (without the word "factor")? And that even though "dilation" means "expansion" or "enlargement", we can use the term in the sense of "contraction" or "reduction" if we leave off the word "factor"?

To me, time dilation is the name of the phenomenon: a particular clock runs at a different rate than reference clocks; for inertial frames in SR, this is more specifically a moving clock runs slow compared to stationary reference clocks. You can mathematically describe this phenomenon in multiple ways. The most common in SR is a a factor saying how many times slower the observed clock is = seconds of coordinate time per second of clock time. However, I was interested in comparing the rates the other way: seconds elapsed on observed clock compared to seconds measured by reference clocks. I was careful to define my terms, so I don't see what the problem is.

[addendum: which is right, "price to earnings ratio" or "earnings to price ratio"? The former is more common, both are used, and both describe the same underlying thing.]

 

[Histspec]

To me, time dilation is the name of the phenomenon: a particular clock runs at a different rate than reference clocks; for inertial frames in SR, this is more specifically a moving clock runs slow compared to stationary reference clocks. You can mathematically describe this phenomenon in multiple ways. The most common in SR is a a factor saying how many times slower the observed clock is = seconds of coordinate time per second of clock time. However, I was interested in comparing the rates the other way: seconds elapsed on observed clock compared to seconds measured by reference clocks. I was careful to define my terms, so I don't see what the problem is.

[addendum: which is right, "price to earnings ratio" or "earnings to price ratio"? The former is more common, both are used, and both describe the same underlying thing.]

Let's write it down that way:
\begin{align}<br /> (1) &amp; &amp; T_{0} &amp; =T&#039;\cdot\gamma\\<br /> (2) &amp; &amp; T&#039; &amp; =T_{0}/\gamma\\<br /> \end{align}

T_0 indicates proper time of a single clock in motion, T indicates coordinate time of two synchronized clocks at rest in S'. T_0 is dilated with respect to coordinate time T.

By the relativity principle, this is symmetrically also true for a single clock at rest in S', which is compared with two synchronized clocks at rest in S:
\begin{align}<br /> (3) &amp; &amp; T&#039;_{0} &amp; =T\cdot\gamma\\<br /> (4) &amp; &amp; T &amp; =T&#039;_{0}/\gamma<br /> \end{align}

 

[PAllen]

Let's write it down that way:
\begin{align}<br /> (1) &amp; &amp; T_{0} &amp; =T&#039;\cdot\gamma\\<br /> (2) &amp; &amp; T&#039; &amp; =T_{0}/\gamma\\<br /> \end{align}

T_0 indicates proper time of a single clock in motion, T indicates coordinate time of two synchronized clocks at rest in S'. T_0 is dilated with respect to coordinate time T.

By the relativity principle, this is symmetrically also true for a single clock at rest in S', which is compared with two synchronized clocks at rest in S:
\begin{align}<br /> (3) &amp; &amp; T&#039;_{0} &amp; =T\cdot\gamma\\<br /> (4) &amp; &amp; T &amp; =T&#039;_{0}/\gamma<br /> \end{align}

Hmm. It looks to me like you have these (consistently) backwards if I understand your convention. If T0 shows 1 second, T' > 1 is expected (for difference of two clocks at rest in s'). You have T' < 1.

 

[nitsuj]

So the precise definition of Time Dilation is the ratio of the Coordinate Time to the Proper Time of a clock moving according to the coordinate frame.

A perfect way to define time dilation; & differential aging is the comparative of elapsed proper times.

 

[PAllen]

A perfect way to define time dilation; & differential aging is the comparative of elapsed proper times.

differential aging is the comparative of elapsed proper times [for two different spacetime paths between some pair of events].

 

[Histspec]

Hmm. It looks to me like you have these (consistently) backwards if I understand your convention. If T0 shows 1 second, T' > 1 is expected (for difference of two clocks at rest in s'). You have T' < 1.

Sorry, I mismatched the symbols. It is

\begin{align}<br /> (1) &amp; &amp; T_{0} &amp; =T&#039;/\gamma\\<br /> (2) &amp; &amp; T&#039; &amp; =T_{0}\cdot\gamma\\<br /> \end{align}

T_0 indicates proper time of a single clock in motion, T indicates coordinate time of two synchronized clocks at rest in S'. T_0 is dilated with respect to coordinate time T.

By the relativity principle, this is symmetrically also true for a single clock at rest in S', which is compared with two synchronized clocks at rest in S:
\begin{align}<br /> (3) &amp; &amp; T&#039;_{0} &amp; =T/\gamma\\<br /> (4) &amp; &amp; T &amp; =T&#039;_{0}\cdot\gamma<br /> \end{align}

 

[Histspec]

In this way, it also becomes clear why length contraction of proper length L_0 is reciprocal to time dilation of proper time T_0:
\begin{align}<br /> T_{0}= &amp; T/\gamma\\<br /> L_{0}= &amp; L\cdot\gamma<br /> \end{align}
The notation is similar to the one used by Max Born, "The theory of relativity", 1962.

 

[nitsuj]

differential aging is the comparative of elapsed proper times [for two different spacetime paths between some pair of events].

That's implicit with proper time and different measures of proper times. Paths is a great word to bring into it, one of those paths is shorter then the other, perhaps contracted (length) depending on the perspective (muon). This is my point why I find it odd length contraction is difficult for some to accept as being "proven" or whatever because it hasn't been "directly" observed, as if time-dilation has in some more "direct" sense. all because of differential aging being thought of as a consequence of time dilation, but not length contraction. It's solid proof of both.

 

[PAllen]

That's implicit with proper time and different measures of proper times. Paths is a great word to bring into it, one of those paths is shorter then the other, perhaps contracted depending on the perspective (muon). This is my point why I find it odd length contraction is difficult for some to accept as being "proven" or whatever because it hasn't been "directly" observed, as if time-dilation has in some more "direct" sense. all because of differential aging being thought of as a consequence of time dilation, but not length contraction. It's solid proof of both.

Except that atmospheric muons reaching the ground provides no evidence for differential aging because it is not an example of it. A muon example that is a differential aging scenario is a muon accelerator ring. Here, you can talk about comparing the time measured on one clock on the rim, with an (imaginary) clock on a muon over one circuit. The two clocks are compared at two events where they are both colocated. This comparison is invariant and would be explained as time dilation in any coordinates (thought different coordinates would disagree about interim rates of the two clocks). Differential aging never has anything to do with length contraction (because all clock comparisons are done at co-location, and no distances are measured).

In the atmosphere muon case, there are no two clocks you can directly compare. Instead, at minimum, you have a clock in the atmosphere at rest relative to the ground, and synchronized with it, another clock on the ground, and the muon clock. This shows time dilation in the Earth frame. In the muon frame, what this shows is that the atmosphere clock co-moving with the ground is out of synch with the ground clock. Thus this tells the muon nothing about why it hits the ground so fast. Instead, for the muon, all of why it reaches the gound is because the ground is close when (per the muon) the muon is created.

This is why time dilation is described as coordinate or frame dependent and is related to length contraction by the fact that what is explained by time dilation in one frame is due to length contraction in another frame. Differential aging is not frame dependent, because all frames explain it as due to different clock rates, and all agree on the amount of difference at the end, and which clock elapsed less time.

 

[nitsuj]

Acceleration doesn't confirm or deny anything, but maybe just forces a particular conclusion if you place lots of emphasis on a clock reading.

postulate...all muons exist for the same amount of time.

Differential aging is frame invariant only because of proximity, comparison of measured proper times.

You don't need an imaginary clock on the accelerator ring muon...the muon is a "clock".

and all agree on the amount of difference at the end, and which clock elapsed less time.

Really? it's because the traveler traveled less length . Looks like allot of emphasis put on the cumulative counting of time to suggest "Ah it was REALLY because the clock was ticking slower", it was equally because it REALLY traveled a shorter length (proper length). unfortunately rulers cannot show the history of measured length quite like a clock does for simple "this current reading less that current reading", that doesn't give anymore physical significance to time dilation over length contraction; in turn does not support time dilation over length contraction as an explanation for differential aging.

 

[PAllen]

Acceleration doesn't confirm or deny anything, but maybe just forces a particular conclusion if you place lots of emphasis on a clock reading.

Acceleration is relevant only to the extent that it enables two spacetime paths between the same events. In SR, this is possible only if one or both world lines have proper acceleration.

postulate...all muons exist for the same amount of time.

Differential aging is frame invariant only because of proximity, comparison of measured proper times.

Yes, this is the key point distinguishing it from time dilation. No auxiliary clocks are needed to measure it, no distances are involved in any interpretation of it.

You don't need an imaginary clock on the accelerator ring muon...the muon is a "clock".

Of course. I just added a little more description.

and all agree on the amount of difference at the end, and which clock elapsed less time.

Really? it's because the traveler traveled less length .

Each considers itself not to have traveled at all, and the other to have traveled. Yet both agree on which clock measures less time at the end, and how much less. This for the atmosphere muon case this is not true at all. The muon thinks the Earth clock has elapsed e.g. only 1 picosecond between the time the muon was born and when the ground clock reaches the muon. Meanwhile, the muon clock has elapsed e.g. 1 nanosecond (a thousand times more than the Earth clock) between birth of muon and hitting ground. Thus, the Earth and muon have opposite conclusions about which clock ran faster and elapsed more time. This is the fundamental distinction between time dilation versus differential aging. I don't get why you are having so much trouble seeing the distinction.

Looks like allot of emphasis put on the cumulative counting of time to suggest "Ah it was REALLY because the clock was ticking slower", it was equally because it REALLY traveled a shorter length (proper length). unfortunately rulers cannot show the history of measured length quite like a clock does for simple "this current reading less that current reading", that doesn't give anymore physical significance to time dilation over length contraction; in turn does not support time dilation over length contraction as an explanation for differential aging.

As explained above, there is no relevance of distance to a twin scenario. In the classic one using uniform acceleration for one of the twins, and Fermi-Normal or Rindler coordinates for this twin, each twin considers the other to have traveled the same distance!

 

[nitsuj]

Thus, the Earth and muon have opposite conclusions about which clock ran faster and elapsed more time. This is the fundamental distinction between time dilation versus differential aging. I don't get why you are having so much trouble seeing the distinction.

I just don't see the muon example as symmetric through out the entire "experiment"; the muon hits the ground, and takes a break checking out this new shared frame with Earth, looks back and says "Wow! I traveled a great Distance through space time. Pretty cool I was able to make it so far through spacetime! Well, maybe I actually didn't travel any great length for any great period of time. Both my measures of time/length were retarded to the specific point I calculated c to the same value as I do in this new Earth frame. Also the spacetime interval, or distance through spacetime, seems to be the same too!"

 

[ghwellsjr]

To me, time dilation is the name of the phenomenon: a particular clock runs at a different rate than reference clocks; for inertial frames in SR, this is more specifically a moving clock runs slow compared to stationary reference clocks. You can mathematically describe this phenomenon in multiple ways. The most common in SR is a a factor saying how many times slower the observed clock is = seconds of coordinate time per second of clock time. However, I was interested in comparing the rates the other way: seconds elapsed on observed clock compared to seconds measured by reference clocks. I was careful to define my terms, so I don't see what the problem is.

The problem is that some people think that both length and time change in the same way for an observer in motion and that is why they continue to measure the speed of light as c. Here are two examples that both came up today:

Length contraction and time dilation are nothing but an explanation for this phenomenon, is what I have known.

Your instrument will calculate speed of light, by using distance of the source and time taken by light to reach it. Since both the values decrease while in motion, when you will calculate the speed, it will turn out to be 'c'.

I just don't see the muon example as symmetric through out the entire "experiment"; the muon hits the ground, and takes a break checking out this new shared frame with Earth, looks back and says "Wow! I traveled a great Distance through space time. Pretty cool I was able to make it so far through spacetime! Well, maybe I actually didn't travel any great length for any great period of time. Both my measures of time/length were retarded to the specific point I calculated c to the same value as I do in this new Earth frame. Also the spacetime interval, or distance through spacetime, seems to be the same too!"

This happens quite often and I think if we emphasized that one is smaller and the other is larger, we can't explain the constant speed of light by simply saying the division comes out the same.

[addendum: which is right, "price to earnings ratio" or "earnings to price ratio"? The former is more common, both are used, and both describe the same underlying thing.]

But applying the value for the "earnings to price ratio" to the "price to earnings ratio" is not right. If you want to use a value less than 1, you should either say that it is the reciprocal of Time Dilation or do what DrGreg said no one does:

"Time" and "rate" are reciprocals of each other, so "rate contraction" means the same as "time dilation". But no-one ever uses the phrase "rate contraction".

 

[PAllen]

I just don't see the muon example as symmetric through out the entire "experiment"; the muon hits the ground, and takes a break checking out this new shared frame with Earth, looks back and says "Wow! I traveled a great Distance through space time. Pretty cool I was able to make it so far through spacetime! Well, maybe I actually didn't travel any great length for any great period of time. Both my measures of time/length were retarded to the specific point I calculated c to the same value as I do in this new Earth frame. Also the spacetime interval, or distance through spacetime, seems to be the same too!"

If the muon 'stops' and 'survives', we are talking about the muon changing its motion, and adopting a new frame at a certain point, corresponding to its changed motion, and using it to analyze its past when its motion was different. This has no bearing on the analysis in the prior frame. Each frame offers a complete, correct analysis of why the muon reaches the ground. If the muon adopts the Earth frame, it is it tautological that its measures now agree with the Earth frame (distance). [Again, in the twin scenario also, all frames offer complete, correct analysis. However, in this case, distances are not part of the explanation in any frame. As I explained previously, in one of the classic twin scenarios (uniform acceleration of one twin), both twins consider the other to have traveled the same distance; both also expect and find that the twin experiencing proper acceleration aged less.]

As for spacetime interval, what interval do you mean? The spacetime interval between muon creation and hitting ground is a timelike interval that is e.g. 1 nanosecond, in all frames. For distance, you have two completely different spacelike intervals involved:

- The one between the event of muon creation and the event on the ground's world line that a ground frame considers simultaneous with muon creation. This measures many kilometers in all frames, being and invariant spacelike interval between two specific events.

- The one between the event of muon creation and the event on ground's world line that the muon travel frame considers simultaneous with the creation event. The creation event is the same event as the prior case. The other event here is a completely different event on the ground's world line. This spacelike spacetime interval is e.g. 10s of meters. The spacetime interval between these two events is also invariant.

 

[nitsuj]

This happens quite often and I think if we emphasized that one is smaller and the other is larger, we can't explain the constant speed of light by simply saying the division comes out the same.

What do you mean "one is smaller and the other is larger"? If I get what you are saying, RoS explains the calculated value of c being invariant. To say that different length is dependent on defining what is simultaneous.

 

[nitsuj]

If the muon 'stops' and 'survives'...


As for spacetime interval, what interval do you mean? The spacetime interval between muon creation and hitting ground is a timelike interval that is e.g. 1 nanosecond, in all frames. For distance, you have two completely different spacelike intervals involved:

- The one between the event of muon creation and the event on the ground's world line that a ground frame considers simultaneous with muon creation. This measures many kilometers in all frames, being and invariant spacelike interval between two specific events.

- The one between the event of muon creation and the event on ground's world line that the muon travel frame considers simultaneous with the creation event. The creation event is the same event as the prior case. The other event here is a completely different event on the ground's world line. This spacelike spacetime interval is e.g. 10s of meters. The spacetime interval between these two events is also invariant.

I can't follow the last two points, The separation between muon creation and landing is time like. I'm not sure why you suggest the muon MUST survive. It "lands", and they have a "fixed" lifespan. Yes, there must be acceleration in with my idealized muon landing, but even with that, the "fixed" lifespan is a pretty solid comparative for a measure of proper time in both frames.

 

[PAllen]

I can't follow the last two points, The separation between muon creation and landing is time like. I'm not sure why you suggest the muon MUST survive. It "lands", and they have a "fixed" lifespan. Yes, there must be acceleration in with my idealized muon landing, but even with that, the "fixed" lifespan is a pretty solid comparative for a measure of proper time in both frames.

You said "the muon hits the ground, and takes a break checking out this new shared frame with Earth, looks back and says...". This is vague, I gave the the interpretation that makes sense to me: the muon stopped. If the muon is considered not to have stopped, then, just because it has reached the ground does not mean it shares a frame with the Earth in normal usage. Normal usage is that the frame of an object is short hand for the frame in which an object is at rest. If the muon doesn't change motion to match the earth, it doesn't share a frame in this sense. In any other sense, I have no idea what you could possibly mean.

I said, so obviously agree, that the timelike interval from muon creation to muon destruction is invariant - same in all frames, and is e.g. 1 nanosecond in all frames. I didn't know what spacetime interval you meant since you did not define it, so I threw out two additional intervals of interest that happen to be spacelike. If you are uninterested in these intervals, fine.

Do you agree that in the muon rest frame:

- the muon ages 1 nanosecond

- the Earth clock will run slow, e.g. elapse much less than 1 nanosecond (< 1 picosecond) between the event simultaneous with muon creation, in this frame, and when the Earth clock reaches the muon. That is, the Earth ages < 1 picosecond in the one nanosecond life of the muon.

- The Earth will have traveled e.g only .3 meters in this frame during the time between creation and destruction of the muon. Thus there is no mystery why the Earth reaches the muon in 1 nanosecond - it has only .3 meters to cover.

Do you agree that in the Earth rest frame:

- the muon ages 1 nanosecond

- the time between creation and destruction is 10 microseconds. That is the Earth ages 10 microseconds between creation and destruction of muon (per this frame).

- the distance traveled by the muon between creation and destruction is e.g. 3 km. The muon reaches the ground because it only ages 1 nanosecond in the 10 microseconds it takes to cover this distance.

In contrast, if twin A is inertial and twin B passes A at some high relative speed, but is uniformly accelerating such that they will meet up with A again later:

- A and B agree on the distance traveled by the other (using the coordinates considered most physical for B).

- A expects and finds that B will age less. B expects and finds that B will age less.

Let's focus on which of these statements you disagree with. If you agree with them all, then we only disagree on how to describe the facts, but not on the facts themselves.

 

[nitsuj]

You said "the muon hits the ground, and takes a break checking out this new shared frame with Earth, looks back and says...". This is vague, I gave the the interpretation that makes sense to me: the muon stopped. If the muon is considered not to have stopped, then, just because it has reached the ground does not mean it shares a frame with the Earth in normal usage. Normal usage is that the frame of an object is short hand for the frame in which an object is at rest. If the muon doesn't change motion to match the earth, it doesn't share a frame in this sense. In any other sense, I have no idea what you could possibly mean.

I said, so obviously agree, that the timelike interval from muon creation to muon destruction is invariant - same in all frames, and is e.g. 1 nanosecond in all frames. I didn't know what spacetime interval you meant since you did not define it, so I threw out two additional intervals of interest that happen to be spacelike. If you are uninterested in these intervals, fine.

Do you agree that in the muon rest frame:

- the muon ages 1 nanosecond

- the Earth clock will run slow, e.g. elapse much less than 1 nanosecond (< 1 picosecond) between the event simultaneous with muon creation, in this frame, and when the Earth clock reaches the muon. That is, the Earth ages < 1 picosecond in the one nanosecond life of the muon.

- The Earth will have traveled e.g only .3 meters in this frame during the time between creation and destruction of the muon. Thus there is no mystery why the Earth reaches the muon in 1 nanosecond - it has only .3 meters to cover.

Do you agree that in the Earth rest frame:

- the muon ages 1 nanosecond

- the time between creation and destruction is 10 microseconds. That is the Earth ages 10 microseconds between creation and destruction fo muon (per this frame).

- the distance traveled by the muon between creation and destruction is e.g. 3 km. The muon reaches the ground because it only ages 1 nanosecond in the 10 microseconds it takes to cover this distance.

In contrast, if twin A is inertial and twin B passes A at some high relative speed, but is uniformly accelerating such that they will meet up with A again later:

- A and B agree on the distance traveled by the other (using the coordinates considered most physical for B).

- A expects and finds that B will age less. B expects and finds that B will age less.

Let's focus on which of these statements you disagree with. If you agree with them all, then we only disagree on how to describe the facts, but not on the facts themselves.

It's the describing of the facts. Even in "scientific literature", I find allot of emphasis is placed on time and it's measurements. Like how you and everything I read say differential aging is due to time dilation. Why not equally length contraction? Because it highlights RoS? (I think that was the same issue with the spacelike interval you mentioned) Maybe because clocks give cumulative sequential readings dependent on it's history. Or maybe some blatantly obvious reason I can't see.

 

[Dale]

It's the describing of the facts.

That is pretty vague. Is there something specific about the description that you don't like, or do you just think that facts shouldn't be described at all, or what?

 

[PAllen]

It's the describing of the facts. Even in "scientific literature", I find allot of emphasis is placed on time and it's measurements. Like how you and everything I read say differential aging is due to time dilation. Why not equally length contraction? Because it highlights RoS? (I think that was the same issue with the spacelike interval you mentioned) Maybe because clocks give cumulative sequential readings dependent on it's history. Or maybe some blatantly obvious reason I can't see.

Can you explain how length contraction is relevant to the twin scenario? In the variant I described, each concludes that the the other has traveled the same distance.

 

[nitsuj]

That is pretty vague. Is there something specific about the description that you don't like, or do you just think that facts shouldn't be described at all, or what?

I went on to explain why, Even in "scientific literature", I find allot of emphasis is placed on time and it's measurements. The context is differential aging, or the muon example.

 

[PAllen]

I went on to explain why, Even in "scientific literature", I find allot of emphasis is placed on time and it's measurements. The context is differential aging, or the muon example.

And these are different situations and you seem very resistant to see the difference. The case of muon's reaching the ground is not differential aging.

 

[nitsuj]

And these are different situations and you seem very resistant to see the difference. The case of muon's reaching the ground is not differential aging.

You're being strictly technical with the use of frames/ comparative coordinates. Is the difference I'm not seeing physical or just about the post analysis?

 

[Dale]

I went on to explain why, Even in "scientific literature", I find allot of emphasis is placed on time and it's measurements. The context is differential aging, or the muon example.

But he didn't do that here. In the description that you objected to he used length just as much as time. He carefully and consistently described both the length and the time in both frames.

So that explanation didn't make sense. In fact, to me it seemed like an unrelated commentary on the scientific literature. I didn't realize you intended it to apply to his comments and now that I understand that was your intention I still don't see the applicability.

 

[PAllen]

You're being strictly technical with the use of frames/ comparative coordinates. Is the difference I'm not seeing physical or just about the post analysis?

I'ts obviously physical. In Twin (differential aging) you have two clocks (or equivalent) that are co-located at two different events. No interpretation is needed to compare them. No matter what frame is used, there is complete agreement about which twin aged more and by how much. [Also, length contraction cannot possibly be relevant because a common twin situation has both twins agreeing on the distance the other traveled - that is each thinks the other twin traveled the same distance, e.g. 1 ly.]

Muon: All you know is that muon reached ground before decaying. You can say the muon aged only a little (this part is invariant - the muon didn't decay). But you can't say (invariantly) that the Earth aged more. In one frame (muon travel frame), the Earth aged much less than the muon between creation and destruction of the muon. The existence of any time dilation at all for the muon depends on choice of frame.

It continues to boggle me how you don't see this difference.

 

[ghwellsjr]

This happens quite often and I think if we emphasized that one is smaller and the other is larger, we can't explain the constant speed of light by simply saying the division comes out the same.

What do you mean "one is smaller and the other is larger"? If I get what you are saying, RoS explains the calculated value of c being invariant. To say that different length is dependent on defining what is simultaneous.

I was reacting to your statement from post #186 where you said:

Both my measures of time/length were retarded to the specific point I calculated c to the same value as I do in this new Earth frame.

I was talking about the Length Contraction factor being less than 1 for a moving observer and the Time Dilation factor being greater than 1 which might dissuade people from jumping to the conclusion that the measurement of the speed of light continues to be c if they think both factors are "retarded", as you put it, or both less than one by the same amount.

To illustrate, let's say that we are measuring the time it takes for light to traverse 10 feet to a mirror and 10 feet back for a total distance of 20 feet. Our timer will read 20 nsecs and we will conclude that the speed of light is 20 feet per 20 nsec or 1 foot per nsec.

If we have a length contracted ruler, say to 50%, then we will think that the distance to the mirror is 20 feet and we will calculate the speed of light to be 40 feet per 20 nsec or 2 feet per nsec.

Instead, if we have a clock that runs 50% slow, then instead of measuring the time interval as 20 nsec, we will say it is 10 nsec and we will calculate the speed of light to be 20 feet per 10 nsec or 2 feet per nsec.

Now if we have both theses problems at the same time, we will calculate the speed of light to be 40 feet per 10 nsec or 4 feet per nsec.

So the the two factors being smaller don't cancel out and don't result in the measured speed of light being the same as before.

So I have to ask you, what did you mean by:

Both my measures of time/length were retarded to the specific point I calculated c to the same value as I do in this new Earth frame.

Also, think about this: the Length Contraction only occurs along the direction of motion. If we're talking about the speed of light at 90 degrees to the direction of motion, then how does your statement apply?

My point is that Length Contraction and Time Dilation are coordinate effects and are easily understood with spacetime diagrams showing the same scenario viewed from different Frames of Reference moving at different speeds. I have shown many examples of this in this thread. In these diagrams, it is obvious that a moving object takes up less distance on the drawing and its clock takes up more distance on the drawing to tick off the same amount of time.