when we start design any circuit we need to know circuit specification.
If you have a 2mv input voltage and 100mv at output you need a amplifier with gain
av = 100mv/2mv = 50[v/v] and zin = 50k and rload >2k.
Is not so easy to meet all this requirements whit this simple amplifier.
So i change them to
voltage gain= 50
load resistance= 10k ohm
vce= 5v
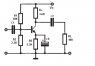
first we need select bjt i choose bc546c with typical hfe = 520 and hfe_min = 420
i start selection from rc resistor.
Rc < 0.1rload = 1kΩ
additional i assume ve = 1v
so
ic = (vcc - vce - ve)/rc = (10v - 5v - 1v)/1kΩ = 4ma
next
re1 = ve/ic = 1v/4ma = 250 but i chose 220Ω
vb = ic*re + vbe = 4ma * 220Ω + 0.65v = 1.53v (voltage at base)
ib = ic/hfe_min = 4ma/420 ≈ 10μa (base current)
r2 = vb / ( 5 * ib) = 30k
r1 = ( vcc - vb) / ( 6 * ib) = 150kΩ
so know if we want voltage gain 50v/v
av = 50 = (rc|| rl) / ( re + (re1||re2) )
( re + (re1||re2) ) = (rc|| rl) / 70 = 909Ω/50 = 18Ω
re = 26mv/ic = 26mv/4ma = 6.5Ω
18Ω = (re + (re1||re2)) = ( 6.5Ω + (220||re2) )
re1||re2 = 18Ω - re = 11.5Ω
re2 = ( 220 * 11.5 ) / (220 - 12.5) = 12.1 = 12Ω.
And now we have a circuit that we can change gain quite easily.
from
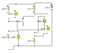
rc/re1 = 1k/220 = 4.5[v/v] if we remove re2 and c2
to
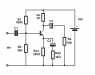
rc/re = 1k/6.5 = 153[v/v] if we short re1.
And normally to meet all your requirements we need to use more practical amplifier circuit or op amp.