zorro
- 1,378
- 0
Homework Statement
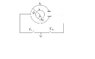
The figure shows two concentric shells of radii R and 2R. A charge q is initially imparted to the inner shell. After the keys k1 and k2 are alternately closed n times, find the potential difference between the shells.
The Attempt at a Solution
Initially, the charge q is induced on the outer shell so that it has -q charge on its inner surface.
When the key k1 is pressed, the outer shell gets earthed.
So the potential which V1 between them is Kq/2R
Now when k2 is closed (after opening k1) the charge q on inner shell disappears so that it gains 0 potential. The charge -q which was induced on the outer surface remains as it is.
Now the potential is given by V2 = -Kq/2R
When k1 is closed again, outer shell gains 0 potential, But the inner shell has an induced charge of +Q. So potential is Kq/2R
In this way, the potential alternates with + and - sign. At the end of 'n', the potential is -Kq/2R
But the answer is Kq/2n+1R
Any hint appreciated.