Power Absorbed In A Electrical Circuit

[gcrawfo2]

Homework Statement

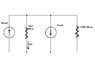
Find the power absorbed by element X, if it is 4000 Ohms.
(See attached picture for circuit)

Homework Equations

KCL: Sum of Currents into Node Must = 0

The Attempt at a Solution

I've already worked through a bunch of these type of problems, but I always mess up on which currents are positive and which ones are negative...which ultimately leads to the wrong answer. I know on this specific problem, the whole idea is to apply KCL in order to obtain a Voltage. That voltage will then be multiplied by 40 Ohms to give you the power absorbed by the resistive element.

I think my lack of understanding of KCL is keeping from getting these ideas. I guess as I run this problem through my head I use a reference location at the node above the 1000 Ohm resistor. And from my thinking I would come up with the following equation...

0=(.08)A - (v/1000[ohms])A - (.03)A - (v/4000[ohms])A

Then I would solve for V, but it ends up giving me the wrong answer. I'm assuming one of my values should be negative?

 

[gcrawfo2]

Nevermind! Figured it out. The equation above is correct, it's when I was adding and subtracting to the opposing sides, I kept seeing .08A as -.08A.

It computes out to 40V on the Resistor. Then I use P=V2/R to obtain .4 Watts.