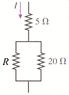Phoenixtears
- 82
- 0
Homework Statement
Consider the circuit in Figure P31.52, in which R = 10 . The 10 resistor is dissipating 48 W of power. How much power are the other two resistors dissipating?
(Image Attached)
5 resistor ________
20 resistor ___24___
Homework Equations
VI=RP
The Attempt at a Solution
I began with the equation VI=RP. Then (I'm not even sure if I can do this!) I assumed the voltage to be constant throughout the resistors (which sounds extremely inaccurate). I was able to solve the equation for power: P= I/R. Then I used the given numbers (10 and 48W) and solved for the current: 480 amps. Placing the 'I' back into the equation I solved using the 20=R. I got the second part right with '24', but am confused why this process doesn't work for a resistor of 5.
Thank you so much in advance!
~Phoenix