- #1
Callmelucky
- 144
- 30
- Homework Statement
- Can you please explain to me why is this the case? Thank you.
- Relevant Equations
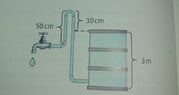
- Hidrostatic pressure = gravitational constant * density * height
Picture below
can someone please explain me why will the water come out of faucet with the pressure of 2000 Pa?
I was expecting the answer to be "water will not come out thrugh the faucet because the pressure from the barrel is not strong enough to overcome the height of the pipe" since pressure depends only on height, gravitational constant and density of liquid, which is in this case water.
Thank you.
can someone please explain me why will the water come out of faucet with the pressure of 2000 Pa?
I was expecting the answer to be "water will not come out thrugh the faucet because the pressure from the barrel is not strong enough to overcome the height of the pipe" since pressure depends only on height, gravitational constant and density of liquid, which is in this case water.
Thank you.
Attachments
Last edited: