Amaelle
- 309
- 54
- Homework Statement
- problem with serie convergence (look at the image)
- Relevant Equations
- taylor serie expnasion, absolute convergence, racine test
Good day
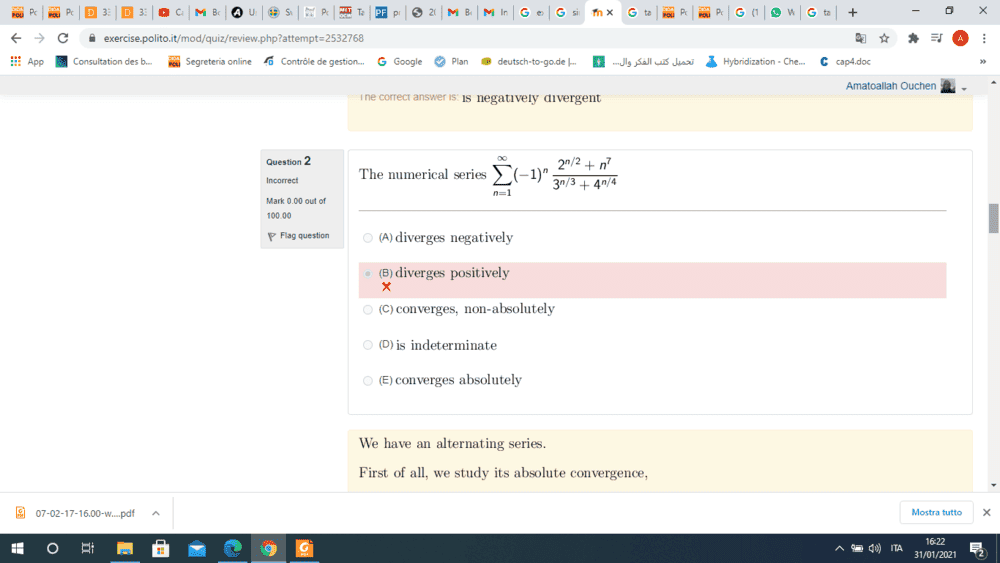
and here is the solution, I have questions about
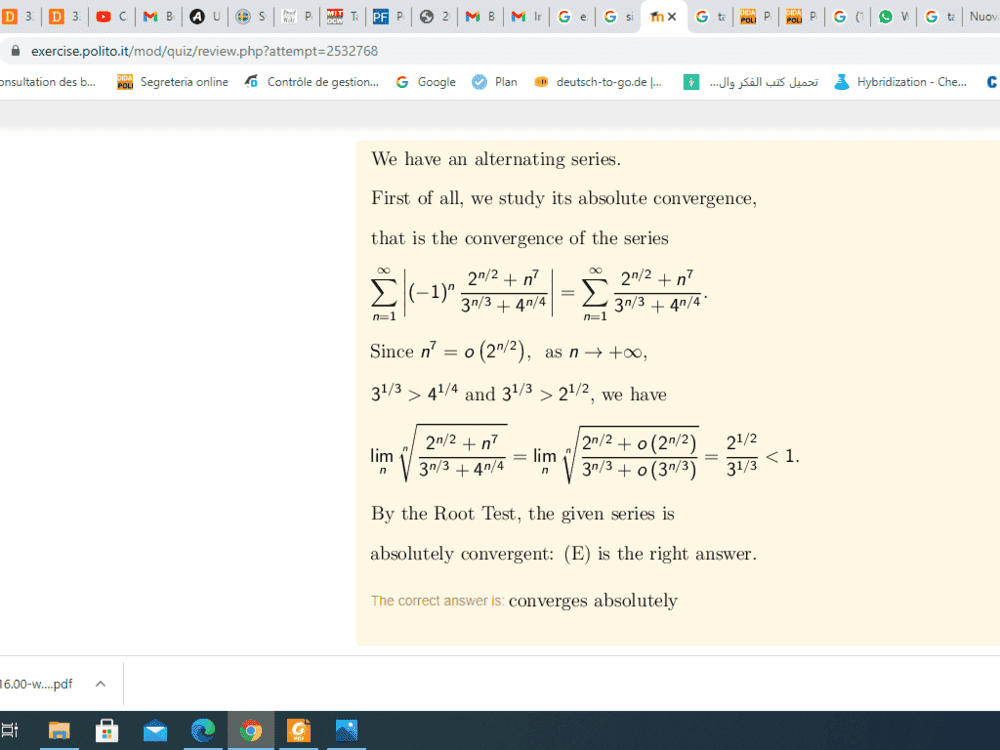
I don't understand why when in the taylor expansion of exponential when x goes to infinity x^7 is little o of x ? I could undesrtand if -1<x<1 but not if x tends to infinity?
many thanks in advance!
and here is the solution, I have questions about
I don't understand why when in the taylor expansion of exponential when x goes to infinity x^7 is little o of x ? I could undesrtand if -1<x<1 but not if x tends to infinity?
many thanks in advance!
Attachments
Last edited by a moderator: