- #1
kshitij
- 218
- 27
- Homework Statement
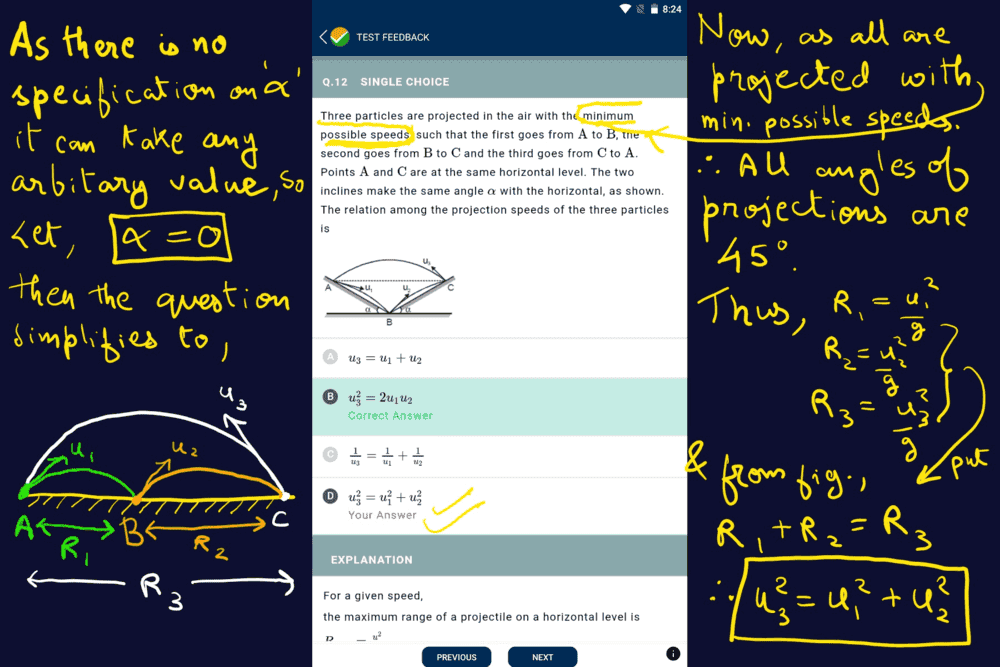
- Three particles are projected in the air with the minimum possible speeds (particle at point A with u1,at B with u2 and at point C with u3), such that the first goes from A to B, the second goes from B to C and the third goes from C to A. Points A and C are at the same horizontal level. The two inclines make the same angle α with the horizontal, as shown. The relation among the projection speeds of the three particles is
(see attachment)
- Relevant Equations
- Range of a projectile=(u^2*sin2α)/g
I know the conventional method for solving this question using the formula for maximum range of a projectile in an inclined plane, but since it is an objective problem, if we consider a non general case where α=0, then clearly we can see that (see attachment) only one option matches which unfortunately isn't the right answer. I would like to know that why doesn't this method work since in the given question there is no restriction on α, it could take any value, so the given answer must be consistent for all values of α. What am I missing, is there a catch in the part that they are projected with minimum possible speed, if so then what should be the condition so that we get the correct answer for the α=0 case?